Беттік интегралдар

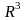-те тегіс D бетін қарастырамыз.Ол өзінің барлық нүктелерін де өзгешеленбеген деп есептейміз,яғни оның 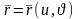,мұндағы 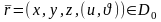параметрлік берілу кезінде оның Якоби матрицасының рангы максималды және екіге тең.Алдымен,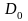 облысы квадрат деп есептейік.Оның ұсақталған V бөлінуді 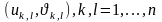таңбасымен тең 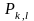квадраттарын аламыз.Мұнда 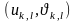нүктесі бұл 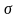қабырғасымен квадратының сол жақ төменгі бұрышының төбесі. квадратына сәйкес келетін D бетінің элементі-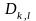 облысын қарастырамыз,яғни 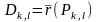.Сондай- ақ , квадратына жауапты,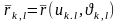 нүктесінде D бетіне жанама жазықтықтың бөлігі- нүктелер жиынын қарастырамыз.D бетінің нүктесінде анықталған, 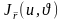матрицасының тиісінше бірінші және екінші бағандары болатын оған жанама екі векторлар 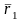және , яғни 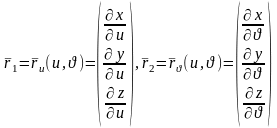.Якоби матрицасының өзгешеленбегендік шартына байланысты ,кез келген 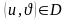нүктесі үшін 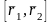векторлық көбейтіндісі нөлден өзгеше.Беттің ерекше нүктесі деп оның мынадай Якоби матрицасының рангы екіден кем нүктесін айтады.

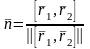векторын қарастырамыз.

Анықтама 1. параметрлеуіне жауапты,D бетіне жүргізілген нормал деп 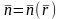векторын айтамыз.Мұндай атау былай берілді,өйткені векторы және векторларының жанамасына перпендикуляр.Дербес жағдайда ,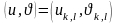 кезінде мынаны аламыз: векторы жазықтығының жанамасына перпендикуляр.Егер квадраты қабырғасының ұзындығы болса,онда параллелограмды бейнелейді және оның 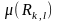ауданы 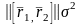- қа тең,мұндағы D векторына жанама және векторлары нүктесінде алынған.Егер D бетінің басқа параметрлеуі берілсе,онда 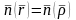немесе 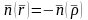теңдіктерінің бірі әрқашан орындалады.Олай болса ,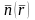 және 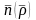векторларының скалярлық көбейтіндісіне тең 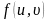функциясы бар болғаны екі мәнді +1 және -1-ді қабылдайды.Бірақ бұл функция -де үзіліссіз.осыдан олне +1-ге тепе-тең,не -1-ге тепе-тең.Бұл параметрлеуді алмастыру кезінде бізбен анықталған D бетіне жүргізілген нормаль D-ның барлық нүктелерінде не өзгермейтінін,не D-ның бірден барлық нүктелерінде өзінің бағытын өзгертетінін білдіреді.Сондықтан,ерекше нүктелерсіз осы тегіс беттің кейбір параметрлеуіне жауапты бетке жүргізілген нормаль онда оның қабырғасын бөледі.Бөлінген қабырғалы бетті екіжақты бет деп атайды

Анықтама 2. Параметрлеудің көмегімен D бетінің бір қабырғасын бөлу D бетін бағдарлау деп аталады.D бетінде үш айнымалы 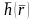функциясы берілген болсын.Ұсақталған V бөлінуге жауапты,келесі төрт интегралдық қосындыны қарастырамыз:

;

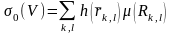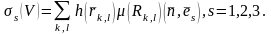
Бұдан,дербес жағдайда ,келесі өрнекті аламыз: мұндағы 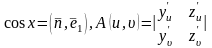. 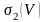және 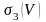үшін өрнекті осыған ұқсас жазуға болады,яғни онда cosx –ты 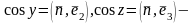ке және A= A(u,υ) -ны 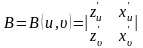, 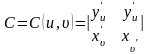ауыстырамыз. нормалының векторын келесі түрде беруге болады: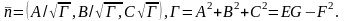

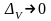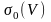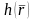Анықтама 3.Егер кезде интегралдық қосындының шегі , онда ол D беті бойынша функцияның бірінші текті беттік интегралы деп аталады.Осы интегралды былай белгілейді:

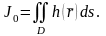
Анықтама 4.Егер кезде,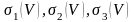 интегралдық қосындыларының шектері , онда оларды 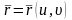параметрлеуге жауапты D бетінің қабырғасы бойынша функцияның екінші текті беттік интегралы деп аталады.Осы интегралдарды былай белгілейді: .

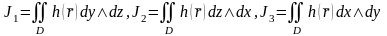Мұндағы 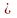таңбасы екінші текті беттік интегралды D жазық жиыны бойынша дағдылы қос интегралдан ажыратуды білдіреді.Бұл таңба жиі алынып тасталады. интегралдарда дифференциалдық түрдің орнына мынадай түрлерді енгізуге болатынын атап өтеміз: және осы дифференциалдық түрдің екінші текті интегралын қарастырамыз.Олардың анықтамасынан тікелей шығатын бірінші және екінші текті интегралдарға енгізілген екі қасиетін келтіреміз.

1)Келесі теңдік дұрыс 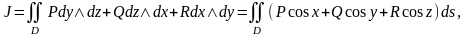мұндағы

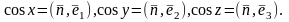
2)Теорема 1.(қос интегралға беттік интегралдың мәлімет туралы) D бетіне компактылы,Жордан бойынша өлшемді ,өзгешеленбеген (ерекше нүктелерсіз), функциясы тегісте үзіліссіз болсын.Онда келесі теңдіктердің орны бар:

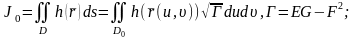
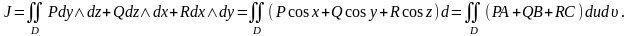Дәлелдеуі.Қисықсызықты интегралдардың айырмашылығы мұнде негізінде ештеңені дәлелдемейді,өйткені интеграл астындағы функция олардың D компактіде үзіліссіздігіне байланысты ,интегралданатын болады.Сондықтан кезде тиісті 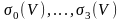интегралдық қосындылар осы интегралдардың мәніне жинақталуға міндетті.Дәлелденді.

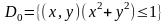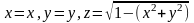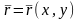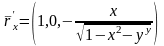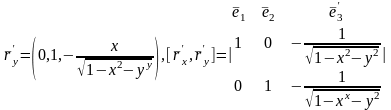
Мысал.1) D бетін ,яғни жоғарғы жарты сфераның “сыртқы келбетін” қарастырамыз.\оны дөңгелегінің бейнесі ретінде бейнелеуі кезінде беруге болады. екенін көрсетейік.Шынында да , параметрлеуі үшін мынаны аламыз: _, .Олай болса 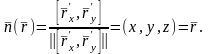Енді .

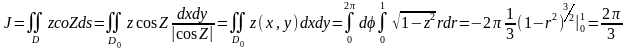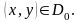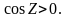Мысал . 2)D беті теңдеуімен берілген болсын , мұндағы - тегіс функция , Интегралдау D бетінің жоғарғы жағы бойынша жүргізіледі,яғни бұл жағдайда Осы жағын 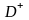арқылы белгілейміз.Сонда