Б1. 1. Множество. Подмножество. Равные множества. Пустое множество. Объединение, пересечение, разность, симметрическая разность множеств. Дизъюктные множества.

Б1. 2. Сравнение множеств. Мощность. Примеры.

Б1. 3. Взаимооднозначное соответствие между множествами.

Б1. 4. Множества меры нуль. Мера пустого множества.

Б1. 5. Свойства внешней меры.

Б1. 6. Измеримые множества

Б1. 7. Операции над измеримыми множествами

Б1. 8. Измеримые функции. Теоремы о функции, заданной на множестве меры нуль и равной константе.

Б1. 9. Арифметические операции над измеримыми функциями

Б1. 10. Эквивалентные функции

Определение 4. Функция f называется эквивалентной функции g (или асимптотически равной ей) при x x₀, если

(x) = 1.

(9.26)

В этом случае пишут f ~ g,   x x₀.

Замечание 1. Если x₀   X, то, как известно, из существования предела  (x) следует, что

(x) =  (x₀). Поэтому в случае (9.24) имеем  (x₀) = 0, а в случае (9.26) -  (x₀) =1. Если f =o(g), x x₀ и  g(x) = 0, то функция f называется бесконечно малой более высокого порядка, чем бесконечно малая g. В случае  f =o(gⁿ), x x₀, бесконечно малую f называют бесконечно малой порядка n относительно бесконечно малой g. 

Замечание 2. Если в условиях определений 3 или 4 функция g не обращается в нуль на множестве x   X   U и x₀   X, то условие (9.24) можно записать в виде

[f(x)/g(x)] = 0,

(9.27)

а условие (9.26) - в виде

[f(x)/g(x)] = 1.

(9.28)

Замечание 3. Если x₀   X, и существует конечный предел

[f(x)/g(x)] = k,

(9.29)

то функция  f(x)/g(x) ограничена на пересечении некоторой окрестности U(x₀) точки x₀ с множеством X т. е. существует такая постоянная c > 0, что для всех x   X   U  выполняется неравенство | f(x)/g(x)| < c, т. е. | f(x)| < c|g(x)|,

откуда следует, что при выполнении условия (9.29) имеет место соотношение

 f(x) = O(g(x)),    x x₀.

Теорема 1. Для того чтобы функции  f(x) и  g(x) были эквивалентны при x 0, необходимо и достаточно, чтобы

f(x) = g(x) + o(g(x)),   x 0.

Б1. 11. Эквивалентность непрерывных функций

Б1. 12. Определение свойства почти всюду

Б1. 13. Сходимость почти всюду

Б1. 14. Простые функции

Б1. 15. Интеграл Лебега простой функции

Мы введем понятие интеграла Лебега сначала для функций, названных выше простыми, т. е. для измеримых функций, принимающих конечное или счетное число значений.

Б1. 16 Равномерная сходимость функциональных последовательностей и рядов

Определение 1. Функциональная последовательность (31.1) называется равномерно сходящейся к функции f на множестве X, если для любого   > 0 существует такой номер n₀, что для всех точек x   X  и всех номеров n > n₀ выполняется неравенство

| fn(x) - f(x)| <  .

(31.7)

Очевидно, что если последовательность (31.1) равномерно сходится на множестве X к функции f, то эта последовательность сходится к функции f на рассматриваемом множестве (определение сходимости последовательности функций на множестве). Если последовательность {f_n} сходится на множестве X к функции f, то пишут f_n    f,

а если эта последовательность сходится равномерно к f на указанном множестве, то пишут f_n    f.

В символической записи определения сходящейся и равномерно сходящейся на множестве последовательности выглядят соответственно следующим образом:

f_n    f     > 0    x   X   n₀     n > n₀:  | f_n(x) - f(x)| <  .

f_n    f     > 0     n₀    x   X     n > n₀:   | f_n(x) - f(x)| <  .

Рис. 124

    Таким образом, если последовательность { f_n} только сходится к функции f на множестве X, то для каждой точки x   X существует, вообще говоря, свой номер n₀ = n₀( ,x), для которого при n > n₀ выполняется неравенство

| f_n(x) - f(x)| <  ,

и может оказаться, что для всех точек x   X невозможно подобрать общий номер n₀, обладающий указанным свойством.      Равномерная же сходимость последовательности { f_n} к функции f означает, что, какое бы число   > 0 ни задать, можно подобрать такой номер n₀, что в любой точке значение функции будет отличаться от значения функции меньше, чем на  (рис. 124).

Лемма 1. Для того чтобы последовательность { f_n} равномерно сходилась на X к функции f, необходимо и достаточно, чтобы

| fn(x) - f(x)| = 0.

(31.8)

    Значение этой леммы состоит в том, что она сводит понятие равномерной сходимости поледовательности { f_n} функций к понятию сходимости числовой последовательности

{ | f_n(x) - f(x)|}

("числовой" в широком смысле этого слова: конечное число членов указанной последовательности может обратиться в + ). В силу этого обстоятельства условие (31.8) часто бывает удобно использовать для выяснения, сходится ли равномерно интересующая нас конкретная последовательность функций.      1. Пусть

f_n    f.

Зададим произвольно   > 0. Тогда существует такой номер n₀, что для всех n > n₀ и всех x   X выполняется неравенство | f_n(x) - f(x)| <  , а следовательно, для всех n > n₀ - неравенство

| f_n(x) - f(x)| <  .

Это и означает выполнение условия (31.8).      2. Пусть выполнено условие (31.8). Зададим произвольно   > 0. Тогда в силу определения предела числовой последовательности существует такой номер n₀, что для всех n > n₀ выполняется неравенство

| f_n(x) - f(x)| <  ,

а следовательно, для всех n > n₀ и всех x   X - неравенство

| f_n(x) - f(x)| <  .

Это означает, что

f_n    f.    

    Следствие. Если существует стремящаяся к нулю последовательность { _n}:

_n = 0.

такая, что для всех x   X выполняется неравенство

| fn(x) - f(x)| <  n,

(31.9)

то последовательность { f_n(x)} равномерно сходится к функции f(x) на множестве X.      Действительно, поскольку неравенство (31.9) выполняется для всех x   X, то

| f_n(x) - f(x)| <  _n,

а поэтому из условия  _n = 0 получаем, что

| f_n(x) - f(x)| = 0.     

    Замечание 1. Очевидно, что из определения равномерной сходимости последовательности функций следует, что если какие-то последовательности равномерно сходятся на некотором множестве, то и любая их конечная линейная комбинация равномерно сходится на этом множестве. 

Б1. 17 ЛЕБЕГА ИНТЕГРАЛ

Одноиз наиболее важных обобщений понятия интеграла. Пусть  - пространство с неотрицательной полной счетно аддитивной мерой   причем  Простой ф у н к ц и е й наз. измеримая функция   принимающая не более счетногомножества значений:  Простаяфункция gназ. суммируемой, если ряд 

сходится абсолютно; сумма этого ряда есть интеграл Лебега:

Функция   суммируема на   если существует равномерно сходящаяся намножестве полной меры к f последовательность простых суммируемых функций g_n и предел 

конечен. Число I есть интеграл Лебега:

Определение корректно: предел I существует и не зависит от выбора последовательности g_n. Если   то I - измеримая почти всюду конечная функция на X. Л. и. есть линейный неотрицательныйфункционал на   обладающий следующими свойствами:

В случае, когда 

интеграл Лебега 

определяется как 

при условии, что этот предел существует и конечен для любой последовательности Е _п такой, что 

 В этом случае свойства 1), 2), 3) сохраняются, а свойство 4) нарушается. Опереходе к пределу под знаком Л. и. см. Лебега теорема. Если Аесть измеримое множество X, то Л. и.

определяется или, как указано выше, заменой Xна А , или как 

где   - характеристич. функция А;эти определения  эквивалентны. Если   для любого измеримого  Если 

 измеримо для каждого п, для 

Обратно, если при тех же условиях на А _n для каждого   и 

то   и верно предыдущее равенство (  -аддитивность Л. и.).

Функция множества 

абсолютно непрерывна относительно   если   то F(А).есть неотрицательная абсолютно непрерывнаяотносительно   мера. Обратное утверждение представляет Радона - Никодима теорему.

Для функций   название "интеграл Лебега" применяется к соответствующему функционалу, если мера   есть Лебега мера;при этом множество суммируемых функций обозначается просто L(Х).иинтеграл 

Для других мер этот функционал наз. Лебега-Стилтьеса интегралом.

Если   - неубывающая абсолютнонепрерывная функция, то 

Если 

-мо-

нотонна на 

и существует точка 

такая, что 

(вторая теорема о среднем).

А. Лебег дал в 1902 (см. [1]) определение интеграла для   и меры   являющейся мерой Лебега. Онстроил простые функции, равномерно приближающие почти всюду на множестве конечной мерыЕизмеримую неотрицательную функцию   и доказал существование общего предела(конечного или бесконечного) интегралов этих простых функций при стремлении их к f. Л. и. является базойдля различных обобщений понятия интеграла. Как отметил Н. Н. Лузин [2], свойство 2) - т. н. абсолютнаяинтегрируемость, выделяет Л. к. для   из всевозможных обобщенных интегралов.

Б1. 18  Интеграл Лебега от ограниченной функции 

     Пусть действительная функция y = f(x) измерима и ограничена на ограниченном интервале [a, b] и A и B - соответственно ее нижняя и верхняя точные границы. Разобъем интервал [A, B], содержащий множество значений функции f(x) на [a, b], на n частей:

A = y₀ < y₁ < y₂ < ... < y_n = B,

и обозначим через S_i множество точек x интервала [a, b], в которых  . Составим две суммы (интегральные суммы Лебега):

 и  .

     Обе интегральные суммы стремятся к одному и тому же пределу, не зависящему от выбора значений y_i, если только наибольшая из разностей y_i- y_i-1 стремится к нулю. Число

есть определенный интеграл от функции f(x) по интервалу [a, b] в смысле Лебега (интеграл Лебега).

Это определение означает, что, каково бы ни было положительное число  , можно указать такое число  , что при любом разбиении интервала [A, B] на части такие, что  , будут справедливы неравенства

 и  ,

а значит, и неравенство

где   (интеграл Лебега можно определить и как предел суммы   ).

Б1. 19 Интеграл Лебега

Пусть   измерима на  .  ф-ции  .    Опр. Ф-ция   наз. интегрируемой на  , если  , а число   наз.интегралом Лебега от ф-ции   по множеству  . Если ф-ция интегрируема, то интеграл всегда существует, т.к   и 

Свойства интеграла Лебега:

1. Если   на  , то    Поскольку  , то   и   и   

2. Если   - интегрируема на  , а   - измерима на  ,   на  , то   - интегрируема на  .

3. Пусть   и   интегрируемы на  . Тогда   имеем   и 

4. Счетная аддитивность интеграла Лебега:

Пусть   интегрируема на   и  ,   измеримые множества. Тогда  , причем ряд абсолютно сходится.

5. Абсолютная непрерывность интеграла Лебега:

Если   интегрируема на  , то    Заметим, что  .

Ввиду аналогичного свойства для неотрицательных функций имеем, что 

Для этого же 

Выберем   так, чтобы   (отсутствие такого   противоречит абсолютной непрерывности интеграла Лебега для неотрицательной функции), тогда, в виду нер-ва (*)

6. Если ф-ция   п.в. на  , то   Если  , то   (док-во этого факта от противного). Следовательно, имеем   на основании свойства для неотрицательных функций.

Если ф-ции   и   равны п.в на  , то  ,   - неотрицательны.) Если   и   просты на  , то, очевидно, свойство выполнено. (ввиду того, что множество на которых у   и   различные значения, имеет меру 0, тогда и сумма, стоящая в определении интеграла Лебега от простой функции, будет одна и та же).   - простую на  . Полагая ее равной 0 на  . Переходя к функции равной   п.в., получили функцию  . Ввиду того, что по предыдущему пункту  , тогда т.в.г. у множеств из определения интеграла Лебега от неотрицательной функции для   и   будут равны.

Б1. 20. Абсолютная непрерывность

Расстановка ударений: АБСОЛЮ`ТНАЯ НЕПРЕРЫ`ВНОСТЬ

АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ - 1) А. н. интеграла - свойство неопределенного интеграла (Лебега). Пусть функция f μ - интегрируема на множестве Е. Интеграл от f на μ-измеримых подмножествах e ⊂ E является абсолютно непрерывной функцией (см. ниже - п. 3) множества относительно меры μ, т. е. для всякого ε > 0 найдется такое δ > 0, что интеграл |∫_e fdμ | < ε для любого множества е с μ (е) < δ. В общем случае интеграл по конечно аддитивной функции множества μ как со скалярными, так и с векторными f или μ, есть абсолютно непрерывная функция.

А. П. Терехин, В. Ф. Емельянов.

2) А. н. меры - понятие теории меры. Мера ν наз. абсолютно непрерывной относительно меры μ, если ν - абсолютно непрерывная функция множества относительно μ. Так, пусть ν - конечная мера, заданная с μ на нек-рой фиксированной σ-алгебре G; тогда ν абсолютно непрерывна относительно μ, если из μ (A) = 0, A ∈ G, следует ν (A) = 0. Обобщенная конечная мера ν абсолютно непрерывна относительно обобщенной меры μ, если ν (A) = 0 как только |μ |(A) = 0, где |μ | - полная вариация μ.

А. П. Терехин.

3) А. н. функции - усиление понятия непрерывности. Функция f(x), определенная на отрезке [а, b], наз. абсолютно непрерывной, если для любого ε > 0, существует такое δ > 0, что для любой конечной системы попарно непересекающихся интервалов (a_k, b_k) ⊂ (a, b), k = 1, 2, ..., n, для которой

справедливо неравенство

Всякая абсолютно непрерывная на отрезке функция непрерывна на этом отрезке; обратное неверно, напр. функция   при 0 < х ≤ 1 и f(0) = 0, будучи непрерывной на отрезке [0, 1], не является на нем абсолютно непрерывной. Если в определении абсолютно непрерывной функции, отбросить требование пустоты попарных пересечений интервалов (a_k, b_k), то функция будет удовлетворять более сильному условию - Липшица условию с нек-рой постоянной.

Если функции f(x) и g(x) абсолютно непрерывны, то абсолютно непрерывны и их сумма, разность и произведение, а если g(x) не обращается в нуль, то и частное f(x)/g(x). Суперпозиция двух абсолютно непрерывных функций может и не быть абсолютно непрерывной. Однако, если функция f(x) абсолютно непрерывна на отрезке [а, b] и А ≤ f(х) ≤ B, х ∈ [а, b], а функция F(у) удовлетворяет условию Липшица на отрезке [А, В], то сложная функция F[f(x)] абсолютно непрерывна на отрезке [а, b). Если абсолютно непрерывная на [а, b] функция f(x) монотонно возрастает, а функция F(y) абсолютно непрерывна на отрезке [f(a), f(b)], то функция F[f(x)] также абсолютно непрерывна на [а, b].

Б1. 21. Теорема Леви

Б1. 22. Лемма Фату

Б1. 23. 24. Теорема Лебега

Б1. 25. Интеграл Римана и Лебега

Пусть на отрезке [a,b] определена вещественнозначная f.

Рассмотрим разбиение отрезка a=x₀<x₁<x₂<... <x_т-1<x_т=b — конечное множество попарно различных точек отрезка. Это разбиение делит отрезок [a,b] на n отрезков [x_i-1,x_i], i=1 ... n. Длина наибольшего из отрезков δR=max(Δ x_i )называется шагом разбиения, где Δx_i = x_i-x_i-1— длина элементарного отрезка.

Отметим на каждом отрезке разбиения по точке ξ_i∋[x_i-1,x_i]. Интегральной суммой называется выражение .

Если при стремлении шага разбиения к нулю интегральные суммы стремятся к одному и тому же числу, независимо от выбора ξ_i∋[x_i-1,x_i], то это число называется интегралом функции f на отрезке [a,b], то есть .

В этом случае, сама функция f называется интегрируемой (по Риману) на [a,b].

Понятие интеграла Римана не пременимо для измеримых функций, которые могут быть разрывны во всей области определения или заданы на таком абстрактном множестве, что понятие интегральных сумм не имеет смысла. В отличие от интеграла Римана, основная идея интеграла Лебега состоит в том, что точки группируются по признаку близости значений функции в этих точках. 

26,27,28,29,30

26. Метрические пространства

27.Открытый шар в метрическом пространстве

27. Открытые множества в метрическом пространстве.

29.Замкнутые множества в метрическом пространстве

30.Топология метрического пространства

Б1. 31. Замыкание множества. Предельная точка

Замыкание множества

Определение 8.1. Точка х называется точкой прикосновения множества А   (Х, τ ), если любая ее окрестность имеет непустое пересечение с А .

Совокупность всех точек прикосновения множества А называется замыканием множества А и обозначается А с чертой.

Операция перехода от множества А к множеству называется операцией замыкания . Любая точка множества А является его точкой прикосновения, но есть точки прикосновения, которые не принадлежат множеству А .

Так, например, замыканием интервала (a , b) является отрезок [a , b], замыканием открытого шара в R ⁿ - замкнутый шар (вместе с ограничивающей его сферой). Замыкание множества Q рациональных чисел на прямой совпадает со всей числовой прямой: .

Из определения замыкания следует также, что замыкание пустого множества пусто, а замыкание всего пространства Х совпадает с Х . Операция замыкания обладает также свойствами:

1. M  ,  М ,

2. Если M  N, то (монотонность замыкания),

3. (идемпотентность).

Предельная точка множества. Предел функции в точке

Пусть  . Число   называется предельной точкой множества X, если

Из определения следует, что любая окрестность точки x₀ содержит точку из множества X, отличную от x₀. Сама точка x₀ может принадлежать, а может и не принадлежать множеству X.

Значение +∞ есть предельная точка множества X, если

Значение -∞ предельная точка множества X, если

Число   называется предельной точкой множества  , если из этого множества можно выделить последовательность (x_n) различных точек, сходящуюся к x₀. (Данное определение и определение, указанное в самом начале эквивалентны)

Б1. 32. Всюду плотное множество.

ВСЮДУ ПЛОТНОЕ МНОЖЕСТВО А топологического пространства А - множество, определяемое свойством: [А] = Х, где [A] - замыкание множества А. Другими словами, в любом открытом в X множестве имеется хотя бы одна точка из множества А. 

Б1. 33. Сепарабельное пространство.

Определение 19.1. Подмножество А топологического пространства (Х, τ) называется всюду плотным в Х, если   = X.

Например, множество рациональных чисел Q всюду плотно в R , так как  .

Определение 19.2. Топологическое пространство (Х, τ ) называется сепарабельным , если в нем содержится счетное, всюду плотное подмножество.

Так, числовая прямая сепарабельна. Сепарабельным является также и n -мерное числовое пространство Rⁿ. Счетным, всюду плотным подмножеством в нем является множество всех точек с рациональными координатами. Несчетное множество точек, наделенное дискретной топологией, несепарабельно.

Теорема 19.1 . Если пространство (Х, τ ) обладает счетной базой, то оно сепарабельно.

Доказательство. Пусть U₁, U₂,... U_n,... - счетная база в Х. Образуем счетное подмножество М = {a_n}, выбрав по одной точке a_i из каждого U_i (i = 1, 2,..., n,...) и докажем, что множество М всюду плотно.  В самом деле, пусть х₀ - произвольная точка из Х, а U₀ - произвольная ее окрестность. По теореме о базе   х₀,  U₀  x₀ U_noиз базы | х₀   U_no   U₀. Но по построению множества М точка a_n0   U_no   U₀. Значит, каждая окрестность U₀ произвольной точки х₀ содержит точку из М, т.е. каждая точка х₀  Х является точкой прикосновения для М . Следовательно,   = Х и М всюду плотно в Х. Теорема доказана.

Б1. 34. Сходящая последовательность.

Последовательность сходящаяся. Числовая последовательность {x_n} называется сходящейся, если она имеет конечный предел 

Последовательность функций (функциональная последовательность) {f_n(x)} называется сходящейся на данном отрезке [a; b] (на интервале (a; b) на множестве M), если числовая последовательность {f_n(x₀)} сходится при всех значениях x₀ из этого отрезка (интервала, множества).

Б1. 35. Фундаментальная последовательность

Фундаментальная последовательность (последовательность Коши, сходящаяся в себе последовательность)  – последовательность  {x_n}, удовлетворяющая следующему условию Коши:

Для любого ε > 0 существует такое n, что для всех n > N, m > N выполняется неравенство |x_n – x_m| < ε.

Здесь x_n – действительное или комплексное число или точка метрического пространства, |x_n – x_m| – расстояние между числами x_n и x_m или между точками x_n и x_m  этого пространства.

Любая сходящаяся последовательность фундаментальна. Пространство, в котором верно и числа  обратное утверждение, называется полным. Множество действительных чисел и множество комплексных чисел – примеры полных пространств, а, скажем, множество рациональных чисел – нет: последовательность рациональных значений , взятых с недостатком (т.е. последовательность 1; 1,4; 1,41; …), сходится, но её предел не является рациональным числом.

Задание. Доказать сходимость последовательности  , используя критерий Коши.

Доказательство. Покажем вначале, что заданная последовательность является фундаментальной, то есть для любого  ,   :   :   :

Таким образом, для любого   существует номер  , а значит рассматриваемая последовательность является фундаментальной, а тогда по критерию Коши она является сходящейся.

Б1. 36. Полное метрическое пространство

Полное метрическое пространство – метрическое пространство, в котором каждая фундаментальная последовательность сходится (к элементу этого же пространства).

В большинство случаев рассматривают именно полные метрические пространства. Для неполных пространств существует операция пополнения, дающая возможность рассматривать исходное пространство как плотное множество в своем пополнении. Операция пополнения во многом аналогична операции замыкания для подмножеств.

Пополнение.

Всякое метрическое пространство можно вложить в полное метрическое пространство таким образом, что метрика – продолжает метрику Х, а подпространство Х всюду плотно в . Такое пространство – называется пополнением Х и обычно обозначается .

Построение.

Для метрического пространства , на множестве фундаментальных последовательностей в Х можно ввести отношения эквивалентности

Можно классов эквивалентности – с метрикой, определенной

,

является метрическим пространством. Само пространство изометрически вкладывается в него следующим образом: точке соответствует класс постоянной последовательности . Получившееся пространство и будет пополнением .

Свойства:

• Пополнение метрического пространства единственно, с точностью до изометрии.

• Полнота наследует замкнутыми подмножествами полного метрического пространства.

• Метрическое пространство компактно тогда и только тогда, когда оно полно и вполне ограничено, то есть для любого 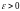пространство можно покрыть конечным числом шаром радиуса

• Топологическим свойством является наличие хотя бы одной полной метрики в классе метрик, порождающих топологию метрического пространства

Примеры:

• Множество вещественных чисел полно в стандартной метрике

• Вообще, любое конечномерное евклидово или унитарное пространство полно

• Свойство полноты является обязательным в определении банахова пространства, в частности гильбертова пространства.

• Пространство непрерывных на отрезке функций с равномерной метрикой является полным метрическим пространством, а потому является банаховым, если рассматривать его как нормированное линейное пространсво.