
- •§3 Свойства определенного интеграла.
- •IV Теорема о среднем.
- •§4. Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
- •§5 Замена переменной в определенном интеграле . Интегрирование по частям
- •§6 Интегрирование по частям в определенном интеграле
- •§7 Интегрирование четных и нечетных функций.
Th5. (Достаточное условие интегр-ти монотонных функций)
Пусть
f(x)
– определена и монотонна на [a,b]
=>
(б/д)
Отметим, что в th5 в неявном виде заложено условие ограниченности функции f(x) на [a,b]
§3 Свойства определенного интеграла.
I) Аддитивность (от лат-го additivus – прибавленный) интеграла, как функции отрезка интегрирования.

(пусть
 ,
тогда
,
тогда
 )
)
(б/д)
Df
1При
a=b
положим
 - интеграл с одинаковыми пределами
интегрирования = 0
- интеграл с одинаковыми пределами
интегрирования = 0
Df
2
При a>b
положим
 , если один из интегралов
, если один из интегралов
 (т.е при перестановке между собой верхнего
и нижнего пределов интегрирования
интеграл умножается на -1)
(т.е при перестановке между собой верхнего
и нижнего пределов интегрирования
интеграл умножается на -1)
Эти определения естественно обобщают введенное ранее определение определенного интеграла. При этом в интегральных суммах нужно ввести понятие ориентированного отрезка и считать, что
 ,
если
,
если

 ,
если
,
если

(2) Пусть f(x) – интегрируема на большем из отрезков [a,b] , [a,c] , [c,b].


а с b
a<c
, a<b
, c<b
(a<c<b)
=> f(x)
интегрируема на
 двух
других отрезках и справедлива формула.
двух
других отрезках и справедлива формула.
 (б/д)
(б/д)
Df
Положим

Для
функции
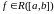 , где a<b
, положим
, где a<b
, положим

Т.е при перестановке между собой верхнего и нижнего пределов интегрирования определенный интеграл умножается на «-1».
II Свойства, связанные с арифметическими действиями над подынтегральными функциями
3) Линейность
Пусть
 и справедлива формула:
и справедлива формула:

Док-во
Возьмем
 .
Тогда
.
Тогда
 ,
тогда:
,
тогда:

 предел
из соответствующего равенства следует
из свойств пределов
предел
из соответствующего равенства следует
из свойств пределов
Замечание. Свойство (3) может быть обобщено на конечную сумму интегрируемых функций
4. Однородность

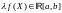
И справедливо равенство:

5)
Пусть
 и
и

а)
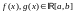
б)
 если
если

Док-во
Возьмем
тогда ,
тогда
,
тогда

Замечание.
Свойство (5а) может быть обобщено на конечное произведение интегрируемых функций
III Некоторые оценки интеграла
Пусть



Доказательство
, составим интегральную сумму:
 используя
свойства пределов (теорема о переходе
к пределу в неравенствах) при
используя
свойства пределов (теорема о переходе
к пределу в неравенствах) при
 ,
перейдем в (*) к пределу и получим:
,
перейдем в (*) к пределу и получим:

Следствие из (6)
Пусть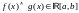 и
и


Доказательство
следует из свойства (6), если обозначить
 и использовать свойство линейности
и использовать свойство линейности

(7)
Пусть
 и
и

Доказательство
Т.к.
,
то
 .
Применяя следствие из теоремы 6 к
неравенствам
.
Применяя следствие из теоремы 6 к
неравенствам
 получим
неравенства:
получим
неравенства:
 ,
которое можно записать как одно
неравенство
,
которое можно записать как одно
неравенство
Т.е. абсолютная величина интеграла от непрерывной функции не больше интеграла от абсолютной величины этой же функции
Следствие из (7)

По свойствам (6) и (7)

(8)
Пусть
 определена
на
определена
на
 за
исключением конечного числа точек
за
исключением конечного числа точек

(б/д).
В частности, отсюда вытекает, что если

Следствие из (8)
Пусть
 за исключением конечного числа точек
за исключением конечного числа точек
 одновременно
или интегрируемы, или не интегрируемы
на
одновременно
или интегрируемы, или не интегрируемы
на
 и,
если интегрируемы, то
и,
если интегрируемы, то

Доказательство
следует из свойства (8) и свойства
линейности
 ,
если положить
,
если положить

Замечание.
Согласно
свойству (8) можно рассматривать интегралы
от ограниченных функций, не определенных
в конечном числе точек
 .
Для этого необходимо доопределить
произвольным образом функцию в
.
Для этого необходимо доопределить
произвольным образом функцию в

IV Теорема о среднем.
Пусть:

Тогда
 ,
что
,
что
 … (1)
… (1)
Док-во.
Отметим,
во-первых
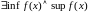
Действительно
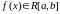 - ограниченная на [a,b]
=>
- ограниченная на [a,b]
=>


 ,
как произведение интегрируемых функций
,
как произведение интегрируемых функций
Положим далее для определенности a<b
И

 .
Другие случаи доказываются аналогично.
.
Другие случаи доказываются аналогично.
Очевидно:

 ,
проинтегрируем это выражение по [a,b]:
,
проинтегрируем это выражение по [a,b]:

Возможны два варианта (из сво-ва (6) )
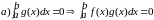
Но
тогда (1) выполняется
 .
.
 Разделим
(2) на
Разделим
(2) на


Следствие. А.
Пусть
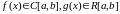 и сохранит знак
и сохранит знак
 :
:

Док-во
Условия св-ва (9) выполнены => справедлива формула (1)
Но
т.к
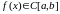 , то по th
о промежуточном значении непрерывных
на отрезке функций
, то по th
о промежуточном значении непрерывных
на отрезке функций
 3)
3)
Следствие. В.
Пусть

Что
 4)
4)
Док-во
=> из свойства (9), если положить

Следствие С.
Пусть

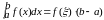 5)
5)
Док-во
следует из следствия А, если положить
 .
Равенство 5) чаще всего называют теоремой
о среднем значении. Оно имеет простой
геометрический смысл.
.
Равенство 5) чаще всего называют теоремой
о среднем значении. Оно имеет простой
геометрический смысл.
Df:
 - называют криволинейной трапецией.
- называют криволинейной трапецией.
прямоугольник
с высотой

где
 равновеликая криволинейная трапеция
с основанием [a,b]
равновеликая криволинейная трапеция
с основанием [a,b]


Замечание.
Помимо
классов функций
 введем классы
введем классы
 ,
где
,
где
 - множество всех функций f(x),
определенных и ограниченных на [a,b];
- множество всех функций f(x),
определенных и ограниченных на [a,b];
 -
множество всех функций f(x),
определенных и монотонных на [a,b].
-
множество всех функций f(x),
определенных и монотонных на [a,b].
Тогда:
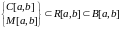 .
.
