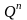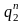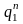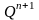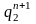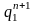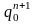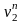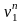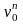Требования к отчету

Отчет должен содержать:

1. Название работы.

2. Краткие сведения о принципе работы триггерных схем, структурную схему универсального триггера.

3. Вариант задания, логическую функцию, выполняемую схемой, таблицу истинности функции, электрическую схему триггера.

4. Распечатку переходного процесса в схеме с расчетом времени задержки сигнала для двух значений нагрузочной ёмкости.

5. Результаты обработки компьютерных расчетов в таблице вида табл.7.4.

Контрольные вопросы

1. Почему триггерные схемы могут служить элементами памяти?

2. В чем отличие асинхронных и синхронных триггеров?

3. Как работают статические триггеры?

4. Принцип работы динамических триггеров.

5. RS-триггер, логическая функция, схема реализации, тактовая диаграмма.

6. D-триггер, логическая функция, схема реализации, тактовая диаграмма.

7. T-триггер, логическая функция, схема реализации, тактовая диаграмма.

8. JK-триггер, логическая функция, схема реализации, тактовая диаграмма.

9. Как из JK-триггера построить D-триггер?

10. Как из JK-триггера построить T-триггер?

11. Как определить быстродействие триггера?

12. Что ограничивает быстродействие асинхронного или синхронного триггера?

13. Что такое состязания, как их устранить?

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Шишина Л.Ю. Основные устройства цифровой микросхемотехники. Часть 2. Учебное пособие. Москва 2013, РИО МИЭТ.

2. Браммер Ю.А., Пащук И.Н. Импульсные и цифровые устройства. М., “Высшая школа”, 1999.

3. Опадчий Ю.Ф., Глудкин О.П., Гуров А.И. Аналоговая и цифровая электроника. М., “Горячая линия - Телеком”, 1999.

4. Алексенко А.Г. Основы микросхемотехники. Лаборатория знаний. М. Бином. 2009.

5. Пухальский Г.И., Новосельцева Т.Я. Проектирование цифровых устройств. Лань, 2012.

Лабораторная работа № 8

Исследование схем Счётчиков

Цель работы: изучение работы и методов построения схем счётчиков.

Теоретические сведения

СХЕМЫ СЧЁТЧИКОВ

Схемы счетчиков весьма широко применяются в различных цифровых устройствах. Основные операции, реализуемые счетчиками, это:

- установка в исходное состояние, на всех выходах сигналы “0”,

- запись информации,

- хранение информации,

- считывание информации.

Основные параметры, которые характеризуют счетчики:

- модуль счета K_сч. Это максимальное число импульсов, которое считывается с выхода после чего счетчик возвращается в исходное состояние, когда на всех выходах появляются сигналы “0”. Величина модуля счета - это еще число устойчивых состояний схемы счетчика;

- быстродействие, которое характеризуется максимальной рабочей частотой входных импульсов и временем установки в исходное состояние;

- деление частоты входного сигнала. В последнем разряде счетчиков частота переключений в K_сч раз меньше входной, поэтому схемы счетчиков используются в качестве делителей частоты.

Различают следующие типы счетчиков:

• суммирующие (инкрементные);

• вычитающие (декрементные);

• реверсивные (с прямым и обратным счетом);

• двоично-кодированные;

• с последовательным переносом (асинхронные);

• с параллельным переносом (синхронные).

Для построения схем асинхронных счетчиков чаще всего используется Т‑триггер, логическая функция которого 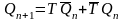. Для построения синхронных счетчиков могут быть использованы любые типы триггеров или их комбинации.

Рассмотрим сначала простой суммирующий счетчик с последовательным переносом. На рис.8.1 показана схема данного счетчика, а на рис.8.2 - тактовая диаграмма работы такого устройства. Схема реализована на трех синхронных Т-триггерах, управляемых срезом тактового сигнала. Начальное состояние счетчика - наличие на выходах всех триггеров состояния “0”. После окончания процедуры счета на всех выходах схемы снова должны установиться нулевые состояния.

Проанализировав полученную тактовую диаграмму счетчика (рис.8.2) можно увидеть, что начиная с первого такта с исходным состоянием на выходах Q₀ = 0, Q₁ = 0, Q₂ = 0, в каждом следующем такте число на выходах увеличивается на 1, при двоичном кодировании получается следующая последовательность:

000001010011100101110111000...

Таким образом, через 8 тактов на всех выходах счетчика установились снова нули, т.е. счет закончился, а значит модуль счета в этой схеме K_сч = 8. Для полных двоичных счетчиков модуль счета рассчитывается по простой формуле

K_сч = 2^п ,

где n - число триггеров в счетчике.

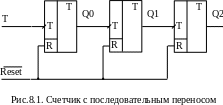
При необходимости прервать программу счета тактовых импульсов в схему приходит сигнал сброса R и на всех выходах устанавливаются “0”. Частота переключений первого триггера самая большая, это частота входного тактового сигнала, частота переключений каждого последующего триггера уменьшается в 2 раза. Первый триггер - это младший разряд числа, а последний - старший разряд. Можно построить на данном счетчике делитель частоты на 2, на 4 и на 8, если снимать данные с выходов Q₀, Q₁, Q₂ соответственно.

Вычитающий счетчик с последовательным переносом показан на рис.8.3, а на рис.8.4 - его тактовая диаграмма.

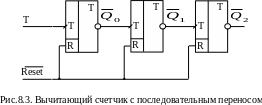
Если вход второго и последующих триггеров в счетчике подсоединить к инверсному выходу предыдущего триггера, на выходах триггеров происходит поразрядное вычитание “по модулю 2”, числа на выходе в каждом такте уменьшаются на 1, что и видно из тактовой диаграммы рис.8.4. Поскольку на тактовые входны триггеров передаются сигналы с инвертированных выходов предыдущих, то срабатывание последнего триггера происходит после срабатывания всех пердыдущих. Модуль счета в этом триггере рассчитывается аналогично предыдущему варианту счетчика

K_сч = 2^п.

Е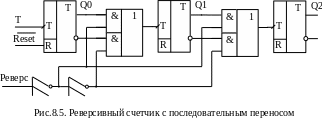 сли в счетчике необходимо проводить прямой и обратный счет, то реализуется структура реверсивного счетчика. Признаком реверсивного переноса является наличие логической схемы управления. Команда на изменение режима счета может быть подана, например, как на рис.8.5.

Счетчик с параллельным переносом. Для ускорения передачи информации применяют счетчики с параллельной организацией обработки данных. Информация в них передается одновременно с выхода каждого триггера на логические элементы, включенные параллельно триггерам (рис.8.6). Задержка в логических элементах меньше, чем в триггерах, поэтому процедура счета происходит быстрее.

Известно несколько способов синтеза двоично-кодированных счетчиков с модулем счета, не являющимся степенью числа 2:

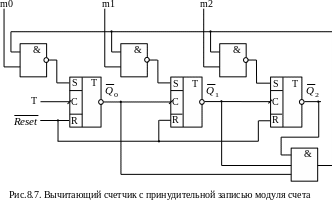
- принудительная запись в триггеры вычитающего счетчика числа M = K_сч  1, определяющего модуль счета, рис.8.7;

- принудительный сброс в суммирующем счетчике после того, как прошло необходимое число тактов, формирующих на выходах триггеров число, заданное как модуль счета, рис.8.8;

- классический метод синтеза функций возбуждения триггеров в счетчиках с параллельным переносом. В этом методе на управляющие входы триггеров подаются сигналы блока комбинационных управляющих схем. Общая структурная схема выглядит, как на рис.8.9. Управляющие функции возбуждения триггеров получаются путем синтеза из таблицы переходов счетчика, (см. пример далее);

- метод исключения лишних состояний. Этот метод является частным случаем классического метода, при котором заранее известные функции возбуждения полного счетчика принудительно переводятся в исходное состояние в моменты достижения числа M = K_сч – 1 в суммирующих синхронных счетчиках (или принудительно переводятся в значение, соответствующее числу M = K_сч – 1 в моменты достижения нулевого значения на выходах вычитающего синхронного счетчика).

Таким образом, при классическом подходе к синтезу функций возбуждения триггеров неполных счетчиков, значения этих функций в “лишних” состояниях могут быть выбраны произвольно (см. пример далее).

В методе исключения лишних состояний фактически изменяется только одно значение в таблице переходов полного счетчика, которое соответствует модулю счета. Причем, необходимо изменять только те функции возбуждения, значения которых в момент окончания счета отличаются от функций возбуждения полного счетчика.

Рассмотрим применение классического метода синтеза управляющих функций на примере синтеза схемы суммирующего счетчика с K_сч = 6, построенного на базе динамического ТV-триггера.

TV-триггер может быть получен из JK-триггера путем объединения входов J и K во вход V. Таблица переходов этого триггера показана в табл.8.1, откуда видно, что вход V является сигналом разрешения на переключение триггера.

Таблица 8.1

Таблица переходов TV-триггера

V (J = K)	Qn	Qn+1
0	0	0
0	1	1
1	0	1
1	1	0

Теперь может быть составлена таблица переходов рассматривемого примера счетчика. В столбцы текущих значений счетчика записывается полный набор чисел Qⁿ, соответствующий разрядности счетчика. В столбцы следующих значений счетчика записываются числа Qⁿ⁺¹, в которые должен переключаться счетчик из соответствующего текущего значения Qⁿ. В столбцы функций возбуждения триггеров записываются значения управляющих сигналов триггера (в данном случае значения сигналов v_i), необходимые для осуществления переключения счетчика из текущего значения Qⁿ в следующее значение Qⁿ⁺¹.

В нашем примере модуль счета счетчика K_сч = 6, т.е. минимальная разрядность счетчика равна 3. При модуле счета K_сч = 6 в рабочем цикле счетчика задействованы числа от 0 до 5, т.е. при текущем значении Qⁿ = 5 следющим значением должно быть Qⁿ⁺¹ = 0. Таким образом, последние два числа 6 и 7 из всех возможных значений трехразрядных двоичных чисел из рабочего цикла исключаются, а в таблице этим значениям Qⁿ можно сопоставить произвольные значения функций возбуждения 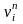(символ “Х” в табл.8.2).

Таблица 8.2

Tаблица переходов суммирующего счетчика с K_сч = 6

Текущее значение счетчика				Следующее значение счетчика				Функции возбуждения
0	0	0	0	1	0	0	1	0	0	1
1	0	0	1	2	0	1	0	0	1	1
2	0	1	0	3	0	1	1	0	0	1
3	0	1	1	4	1	0	0	1	1	1
4	1	0	0	5	1	0	1	0	0	1
5	1	0	1	0 (6)	0 (1)	0 (1)	0 (0)	1 (0)	0 (1)	1 (1)
6	1	1	0	– (7)	– (1)	– (1)	– (1)	Х (0)	Х (0)	Х (1)
7	1	1	1	– (0)	– (0)	– (0)	– (0)	Х (1)	Х (1)	Х (1)

Примечание. В скобках указаны значения для полного счётчика с K_сч = 8.

После заполнения таблицы переходов счетчика и доопределения значений функций возбуждения, сответствующих “лишним” значениям Qⁿ можно по картам Карно синтезировать три логические функции , каждая из которых зависит от набора значений .

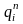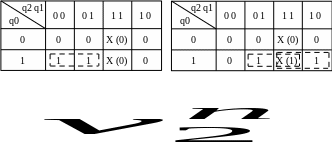
В результате получаем следующий набор логических функций

; ; .

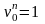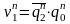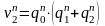Теперь можно получить схему счетчика, показанную на рис.8.11

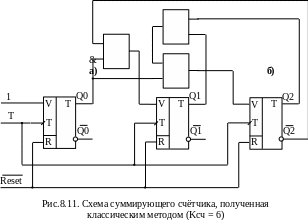
В заключение рассмотрения классического метода синтеза счетчиков, можно сказать, что этот метод может быть использован для синтеза последовательностных устройств с произвольной таблицей переходов, построенных на любом типе динамических триггеров.

Метод исключения “лишних” состояний поясним также на примере суммирующего счетчика с K_сч = 6.

В [2] показано, что в полных суммирующих счетчиках, построенных на динамических TV-триггерах управляющие функции V(Q) определяются как

.

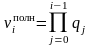В рассматриваемом примере, для получения K_сч = 6 в таблице переходов полного счетчика требуется изменить значения функций возбуждения в строке, соответствующей Qⁿ = 5. В табл.8.2 значение функции возбуждения V = 101₂. Значение функции возбуждения полного счётчика V^полн = 011₂ в табл.8.2 указано в скобках. Значения V^полн и V отличаются старшими двумя разрядами и, для получения модуля счета K_сч = 6, требуется изменить значения функций возбуждения только для триггеров двух старших разрядов.

Введем функцию 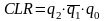, которая равна “1” только при Qⁿ = 5 (101₂). Тогда необходимое изменение функций возбуждения v можно выразить следующим образом:

v = v^полн + CLR, при v^полн = “0”, a v = “1”;

v = v^полн  CLR, при v^полн = “1”, a v = “0”.

В случае K_сч = 6, V^полн = 011₂ и V = 101₂:

;

.

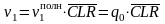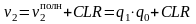Функцию v₀ изменять не требуется.

Соответствующая схема счетчика изображена на рис.8.12.

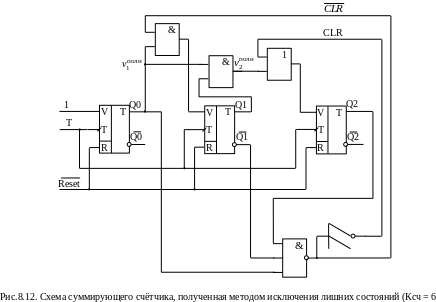
Число импульсов, поступающих на вход счётчиков, отображается на выходе в двоичном коде. В ряде случаев необходимо, чтобы каждому входному импульсу соответствовал сигнал на единственном из выходов устройства (унитарный код, код ”1 из N”). С наименьшими затратами данная задача решается при использовании кольцевых счётчиков (рис.8.13), представляющих собой сдвиговый регистр, выход последнего разряда которого подсоединён к входу первого разряда.

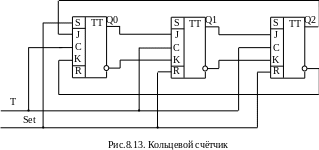
Рис.8.14. Тактовая диаграмма кольцевого счетчика

По сигналу установки “Set” все триггеры, кроме первого, устанавливаются в состояние “0”, а в первый записывается “1”. По первому тактовому импульсу “1” из первого триггера переписывается во второй, в первый - из последнего разряда записывается “0”. По второму импульсу “1” из второго триггера переписывается в третий, уступая место “0” из первого. Тактовая диаграмма работы устройства показана на рис.8.14.

Все представленные схемы реализованы в базисе И-НЕ. Замена базиса на ИЛИ-НЕ приводит к инверсии уровней управляющих сигналов триггеров.

ДОМАШНЕЕ ЗАДАНИЕ

1. Изучить описание работы схем счётчиков.

2. Определить вариант индивидуального задания (табл.8.3).

3. Подготовить входные файлы для моделирования по варианту электрической схемы счётчика на программе Orcad в соответствии с данными варианта. Для получения TV-триггеров использовать JK-триггеры по схеме “M-S”.

ЗАДАНИЕ НА ЛАБОРАТОРНУЮ РАБОТУ.

1. Провести моделирование работы заданной схемы счётчика.

2. Для указанного варианта подготовить задание для моделирования работы схемы на ЭВМ при помощи программы Orcad.

3. Провести расчеты переходных процессов в заданной схеме счётчика.

4. Провести измерения динамических параметров схемы t_фр, t_ср, t_зд01, t_зд10.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

1. Подготовить задание для моделирования работы схемы в Orcad.

2. Провести расчет переходных процессов на частоте тактового сигнала

f  = 1 МГц, оценить максимальную частоту работы схемы.

3. Провести моделирование на максимальной частоте и распечатать результаты моделирования.

Таблица 8.3