Контрольная работа № 4 Задача № 364. Исследовать ряд на сходимость (а, б) и найти интервал сходимости (в)

Решение:

Исследуем ряд по необходимому признаку:

Посмотрим поведение функции

Или используем разложение в ряд:

Общий член U_n стремится к нулю при значит, по необходимому признаку исходный ряд сходится.

Необходимый признак выполняется. Необходимо продолжить исследование по достаточным признакам.

Так как функция при х ≥ 1 является непрерывной, положительной и монотонно убывающей, то можем воспользоваться интегральным признаком Коши: . Находим:

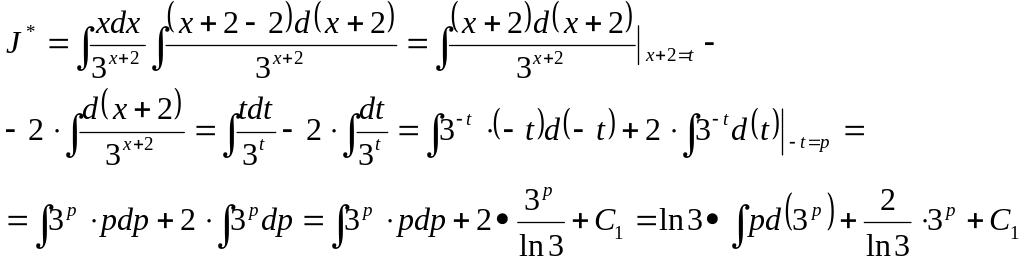
Используем интегрирование по частям:

Положим тогда

Несобственный интеграл расходится, а, следовательно, вместе с ним расходится исходный ряд.

ОТВЕТ: Ряд расходится

Решение:

Имеем знакочередующийся ряд. Воспользуемся признаками Лейбница сходимости знакочередующегося ряда.

1) Очевидно, что по необходимый признак выполняется для данного ряда:

2) Выполняется.

Рассмотрим ряд, составленный из абсолютных членов исходного ряда:

Имеем гармонический ряд, который расходится.

Действительно, так как функция при х ≥ 1 является непрерывной, положительной и монотонно убывающей, то можем воспользоваться интегральным признаком Коши: . Находим:

Несобственный интеграл J расходится и, следовательно, вместе с ним расходится ряд В₍₊₎.

ОТВЕТ: Ряд сходится условно

Решение:

Для определения области сходимости функционального ряда используем признак Даламбера числового ряда, при этом предел вычисляется от выражений функционального ряда взятых по модулю:

Исследуем ряд на концах найденного интервала (подставляем значения концов интервала в функциональный ряд).

При x = 1 получаем ряд:

Гармонический ряд, который расходится (показано в предыдущем примере)

Таким образом,

область сходимости исходного ряда С: − 1 < x < 1

Задача № 384. Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда

Решение:

Используем разложение функции в ряд Маклорена:

В нашем случае:

Тогда

Для обеспечения заданной точности ε=0,001 достаточно взять два первых члена ряда. Третий член по абсолютной величине < ε, и начиная с этого члена и далее, ряд можно отбросить. Этот расчет основан на свойстве знакочередующегося ряда: при замене ряда частичной суммой происходит ошибка, не превышающая по абсолютной величине значения первого из отброшенных членов. Если при вычислениях степенной ряд окажется знакопостоянным, то обеспечение заданной точности вычислений нужно производить по оценке остаточного члена в форме Лагранжа: который позволит выбрать необходимое число членов ряда.

Таким образом, получаем:

Задача № 404. При указанных начальных условиях найти три первых, отличных от нуля, члена разложения в степенной ряд функции являющейся решением заданного дифференциального уравнения