Содержание

Задача № 224. Вычислить частные производные первого и второго порядка от заданных функций 2

Задача № 244. Найти экстремум заданной функции 3

Задача № 264. Требуется: 1) Построить в плоскости ХОУ область интегрирования заданного интеграла; 2) изменить порядок интегрирования и вычислить площадь области при заданном и измененном порядке интегрирования. 5

Задача № 284. Криволинейный интеграл 6

Задача № 304. Найти общее решение дифференциального уравнение первого порядка 9

Задача № 324. Найти частное решение дифференциального уравнение второго порядка с начальными условиями 11

Задача № 364. Исследовать ряд на сходимость (а, б) и найти интервал сходимости (в) 15

Задача № 384. Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда 18

Задача № 404. При указанных начальных условиях найти три первых, отличных от нуля, члена разложения в степенной ряд функции являющейся решением заданного дифференциального уравнения 20

Задача № 464 23

Задача № 504 26

КОНТРОЛЬНАЯ РАБОТА_ПРИКЛАДНААЯ МАТЕМАТИКА 27

Задача № 224. Вычислить частные производные первого и второго порядка от заданных функций

(*)

Решение:

Задача № 244. Найти экстремум заданной функции

(*)

Решение:

1. С помощью необходимого существования экстремума, т.е. из системы

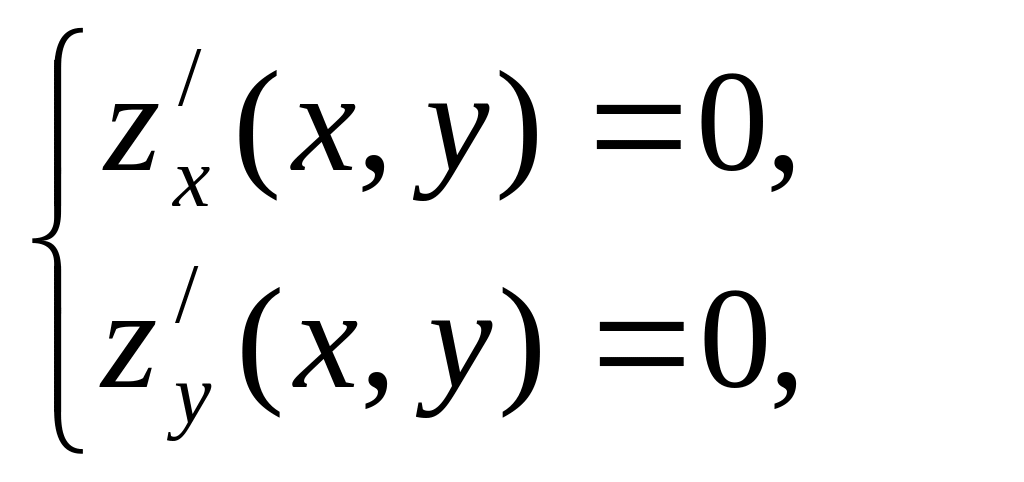найдем координаты стационарных (критических) точек:

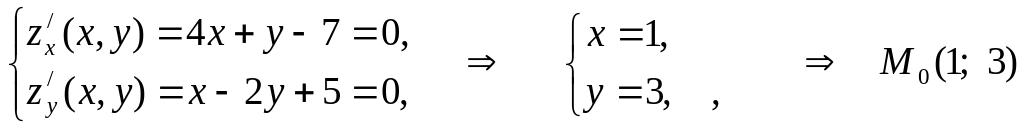
Получили систему двух уравнений, которую решаем методом Гаусса с помощью MS Excel:

A1*X1	A2*X2	A3*X3	A4*X4	B1
A1	A2	A3	A4	B1
4	1	0	0	7
1	-2	0	0	-5
1	0,25	0	0	1,75
0	-2,25	0	0	-6,75
1	0,25	0	0	1,75
0	1	0	0	3
1	0,25	0	0	1,75		X1=	1,00
0	1	0	0	3		X2=	3,00

2. Проверим выполнение достаточного условия существования экстремума в стационарной точке M₀(0;0). Для этого составим

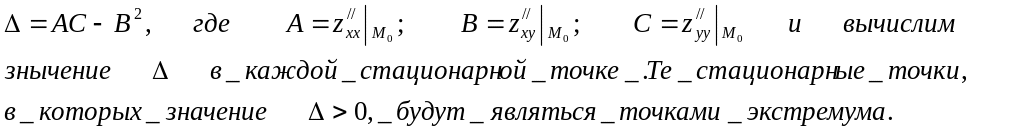
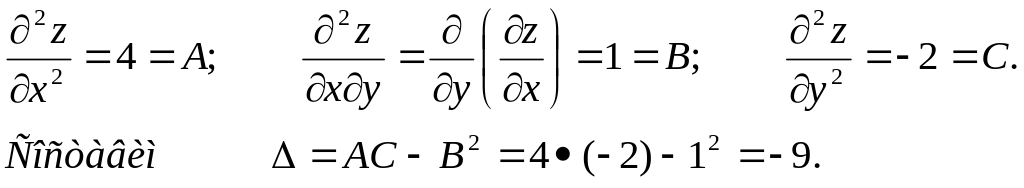
2. Решим вопрос о характере экстремума.

• если то точка M₀ (x,y) будет точкой максимума, если A (M₀) < 0 (или C (M₀) < 0), и точкой минимума, если A (M₀) > 0 (или C (M₀) > 0);

• если то в точке М₀ экстремума нет (достаточные условия наличия или отсутствия экстремума);

• если то требуется дальнейшее исследование (сомнительный случай).

В данном случае получили:

В точке М₀ экстремума нет

Задача № 264. Требуется: 1) Построить в плоскости ХОУ область интегрирования заданного интеграла; 2) изменить порядок интегрирования и вычислить площадь области при заданном и измененном порядке интегрирования.

(*)
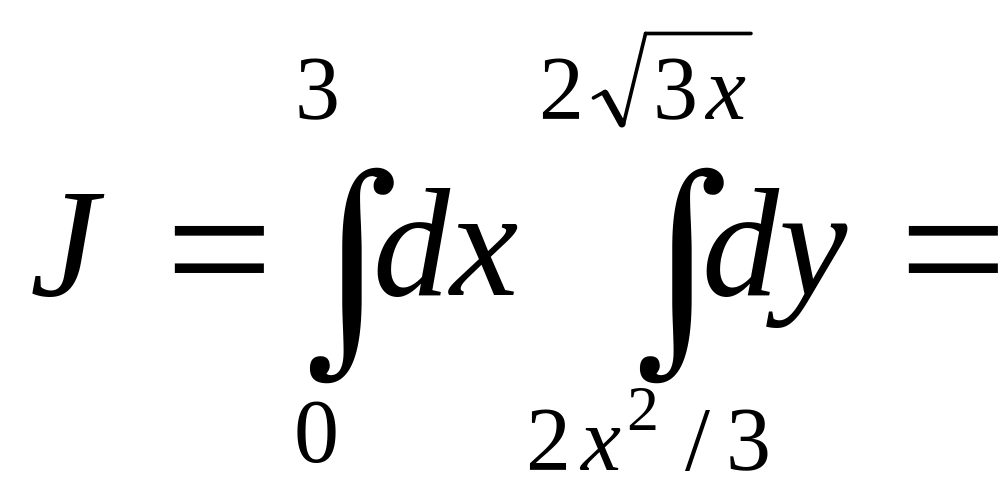