4. Методика решения задач

Последовательность разработки Сгр ТЭП рассмотрим на примере планирования одного из видов технического обслуживания (ТО) подвижной дизельной электростанции (ДЭС).

Допустим, что необходимо выполнить ТО подвижной ДЭС. Обслуживанию подлежат: шасси агрегата, топливный бак, агрегатный отсек в котором расположены дизель-генераторы, и операторный отсек, в котором размещается оборудование управления электростанцией и вспомогательное оборудование. В соответствии с эксплуатационной документацией на агрегат необходимо выполнить следующий перечень операций (работ) ТО с трудозатратами (Ф_ТО, чел. - ч) на проведение каждой из них:

работа № 1: распломбирование агрегата ( Ф₁=0,1 чел. - ч);

работа № 2: прочистка сливного отверстия топливного бака (Ф₂=0,1 чел. - ч);

работа №3: техническое обслуживание шасси агрегата

(Ф₃=1 чел. – ч);

работа № 4: проверка исходного положения оборудования агрегата (Ф₄=2,2 чел. - ч);

работа № 5: проверка уровня масла в топливном насосе и регуляторе (Ф₅=0,6 чел. - ч);

работа №6: проверка щеток и контактов колец генераторов

(Ф₆=2 чел. - ч);

работа № 7: замена аккумуляторных батарей (Ф₇=1,5 чел. - ч);

работа №8: техническое обслуживание заземляющих устройств (Ф₈=0,5 чел. - ч);

работа № 9: техническое обслуживание радиостанции и переговорного устройства (Ф₉=1 чел. - ч);

работа №10: проверка ЗИП (Ф₁₀=6 чел. - ч);

работа №11: проверка работы дизель-агрегатов (Ф₁₁=1 чел. - ч);

работа №12: проверка эксплуатационной документации

(Ф₁₂=0,5 чел. - ч);

работа №13: пломбирование агрегата (Ф₁₃=0,33 чел. - ч).

Обслуживание агрегата выполняется двумя расчетами: расчетом обслуживания шасси (РШ) в количестве 4 человек и расчетом обслуживания специальной части агрегата (РСЧ) в количестве 4 человек. Первый расчет, согласно своему предназначению, может выполнять работы №1,2,3,7,13, а второй расчет – работы № 4,5,6,8,9,11,12. Проверка ЗИП (работа №10) выполняется совместно обоими расчетами.

Работы на агрегате начинаются с распломбирования агрегата, а завершаются пломбированием агрегата. Работа по проверке ЗИП проводится после обслуживания шасси и замены аккумуляторных батарей. В свою очередь, проверка работы дизель-агрегатов может проводиться после обслуживания составных частей агрегата, а проверка эксплуатационной документации – после проверки работы дизель-агрегатов. Директивное время выполнения работ составляет 3 часа.

Разработаем Сгр проведения работ ТО подвижной ДЭС с использованием метода сетевого планирования.

Методика выполнения задачи 1

1. Составление таблицы работ. На основании словесного описания ТЭП составим таблицу работ по предлагаемой схеме, представленной на рис.1.3.

Для определения продолжительности работ воспользуемся выражением:

, (1.1)

где t ( i, j ) – продолжительность работы; Ф _{i, j} – трудозатраты на проведение ( i, j )–й работы; n _{i, j} – количество исполнителей ( i, j ) –й

работы.

Продолжительность работ в графе 6 указывается в часах и минутах. Допускается указывать продолжительность работ в целых и десятых частях с обязательным их учетом при проведении дальнейших расчетов и выборе масштаба построения ортогональной формы Сгр.

Графы 1, 2, 3, 4 заполняются исходя из словесного описания ТЭП. При определении количества исполнителей и кода предшествующей работы в словесном описании ТЭП необходимо выделить перечень работ, которые могут выполняться номерами расчетов параллельно (начало работ одновременно), а какие только последовательно исходя из технологии их выполнения (например, операции тройного контроля), ограничений на личный состав или трудозатраты.

Таблица работ планируемого ТЭП представлена на рис.1.3.

2. Построение и расчет временных параметров Сгр.

Осуществить построение Сгр в пять этапов:

• построить черновой вариант Сгр;

Код работы аi	Наименование работы	Кто проводит работы	Трудозатраты, чел. - ч	Кол-во исполн., чел.	Продолжи- тельность работы, ч	Код предшеству- ющей работы
а1	Распломбирование агрегата	РШ	0.1	1	0.06	-
а2	Прочистка сливного отверстия топливного бака	РШ	0.1	1	0.06	а1
а3	Техническое обслуживание шасси агрегата	РШ	1.0	2	0.30	а1
а4	Проверка исходного положения оборудования агрегата	РСЧ	2.2	2	1.06	а1
а5	Проверка уровня масла в топливном насосе и регуляторе скорости	РСЧ	0.6	2	0.18	а1
а6	Проверка щеток и контактов колец генераторов	РСЧ	2.0	2	1.00	а5
а7	Замена аккумуляторных батарей	РШ	1.5	2	0.45	а3
а8	Техническое обслуживание заземляющих устройств	РСЧ	0.5	2	0.15	а4
а9	Техническое обслуживание радиостанции и переговорного устройства	РСЧ	1.0	2	0.30	а6
а10	Проверка ЗИП	РШ, РСЧ	6.0	4	1.30	а7, а8
а11	Проверка работы дизель-агрегатов	РСЧ	1.0	2	0.30	а9
а12	Проверка эксплуатационной документации	РСЧ	0.5	2	0.15	а11
а13	Пломбировка агрегата	РШ	0.33	2	0.10	а2, а10 а12

Рис.1.3. Таблица работ проведения технического обслуживания подвижной ДЭС

• провести упрощение чернового варианта Сгр и провести нумерацию событий;

• провести построение Сгр в полигональной форме и рассчитать его основные временные параметры;

• провести построение Сгр в ортогональной форме с учетом продолжительности действительных работ и ожиданий и рассчитать его дополнительные временные параметры;

• провести анализ Сгр и проверку правильности его построения.

Для ТЭП, включающего незначительное количество работ, можно построить Сгр непосредственно по таблице работ. Если количество работ значительно и они имеют сложные взаимосвязи, то для построения Сгр следует воспользоваться формальным способом, базирующимся на использовании понятия «фиктивная работа». Для решения нашей задачи рассмотрим этот способ.

I этап. Составление чернового варианта Сгр.

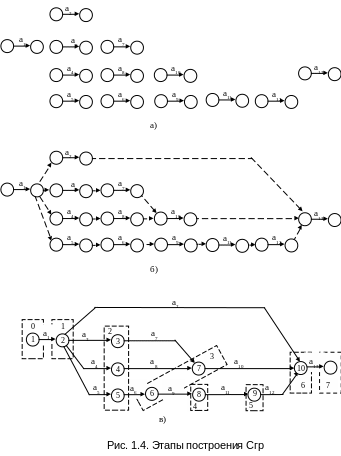
На этом этапе, проанализировав таблицу работ, изобразим эти работы графически в виде сплошных безмасштабных стрелок со своими событиями так, чтобы они (работы) располагались на некотором расстоянии друг от друга и в приблизительном соответствии с последовательностью их выполнения. Для нашего примера черновой вариант Сгр представлен на рис.1.4, а. При помощи пунктирных стрелок (фиктивных работ) изобразим в соответствии с таблицей работ взаимосвязи между работами (рис.1.4, б). На данном этапе построения Сгр появляется первый, черновой его вариант, который подлежит дальнейшей корректировке и перестройке.

II этап. Упрощение чернового варианта Сгр и нумерация

событий.

На втором этапе с целью сокращения количества событий в графике объединим начальные и конечные события тех фиктивных работ, исключение которых не приведёт к изменению взаимозависимостей между действительными работами отображаемого ТЭП и нарушению правила изображения параллельных работ (рис.1.4, в). Чтобы избежать ошибок при упрощении чернового варианта Сгр, необходимо соблюдать следующие правила:

1. В сетевой модели не должно быть работ, имеющих одинаковые обозначения, т.е. работ с общими начальными и конечными событиями (рис. 1.5, а).

Для того чтобы различать такие работы, необходимо ввести дополнительные события и фиктивные работы.

2. Если для выполнения одной из работ (например, 3,4 – рис. 1.5, б) необходимо получение результатов всех работ, входящих в начальное для нее событие 3, а для другой работы 3,5 – только одной из этих работ (например, 2,3), то в сеть должно быть введено новое событие 3^/,отражающее результат работы 2,3, и фиктивная работа 3^/,3, связывающая новое событие с прежним.

3. Если некоторые работы (например, 2,4 и 2,5 на рис. 1.5, в) могут быть начаты после частичного выполнения предшествующей им работы 1,2, то эту предшествующую работу следует разбить на части и ввести дополнительные события 2' и 2", означающие завершение соответствующих частей работы 1,2, и из них начало работ 2', 3 и 2", 5.

4. В Сгр не должно быть замкнутых контуров, т.е. путей, соединяющих некоторое событие с самим собой (рис. 1.5, ж). Наличие такого контура в Сгр указывает на случайную или логическую ошибку, которая должна быть устранена.

5. В Сгр не должно быть "тупиков", т.е. событий (кроме завершающего), из которых не выходит ни одна работа (например, событие 3 и работа 2', 3 (на рис. 1.5, б), которую можно трактовать как тупиковую). Наличие "тупиков" в сети свидетельствует либо об ошибке, либо о том, что результаты этой работы далее никому не нужны, и она в процессе является лишней.

6. В Сгр не должно быть "висячих" работ, т.е. таких, в начальное событие которых не входит ни одна работа (если это событие не исходное для процесса). Наличие "висячих" работ (или "обрывов" в сети) означает, что результат, необходимый как исходное условие для начала выполнения работы, никому не задан, а следовательно, данное событие свершиться не может. При обнаружении "обрыва" в Сгр необходимо определить исполнителей работ, обеспечивающих свершение этого события, и включить эти работы в сеть.

7. При построении Сгр необходимо избегать взаимного пересечения стрелок (рис. 1.5, г).

8. Если внутри сети можно выделять некоторую подсеть, планирование которой может быть произведено независимо от всей сети, то целесообразно Сгр укрупнить путем замены данной подсети одной

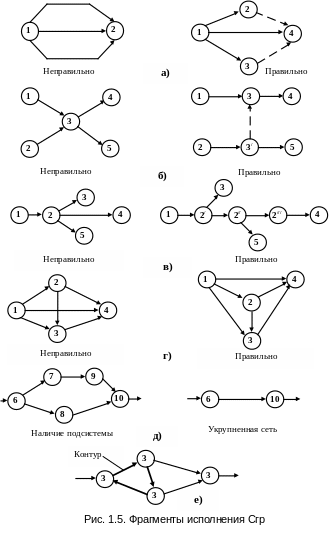
работой продолжительностью, равной максимальному времени выполнения работ подсети. Пример укрупнения сети показан на

рис. 1.5, д.

После завершения упрощения Сгр проверяем соблюдение вышеперечисленных правил построения модели и при отсутствии ошибок все события размещаем в цепочки по «ярусам» (по строкам для лучшего чтения). Таким образом, наш упрощенный вариант Сгр готов к проведению нумерации событий.

Для простых сетей, выполненных в ортогональной форме, нумерацию событий осуществляют слева – направо и сверху – вниз с учетом моментов наступления событий.

Для черновых вариантов Сгр и сетей, выполненных в полигональной форме, используют метод "вычеркивания" дуг. Сущность метода применительно к нашей задаче поясним с помощью рис.1.4, в.

Исходному событию присваиваем 0-ранг и зачеркиваем (условно) все выходящие из него стрелки. 1-ранг присваиваем событиям, в которые входят только вычеркнутые стрелки. В данном случае такое событие оказалось одно, поэтому ему присваиваем 1-ранг. Далее зачеркиваем все стрелки, выходящие из события 1-ранга. Событий, в которые входят только зачеркнутые стрелки, оказалось три, и им присваиваем 2-ранг. Так продолжаем ранжирование до конечного события. После ранжировки событиям присваиваем номера в порядке возрастания их рангов. События одного ранга нумеруются сверху - вниз.

III этап. Построение Сгр в полигональной форме и расчет

основных временных параметров.

К построению Сгр в полигональной форме приступают после нумерации событий. Кружки, обозначающие события рисуют, одинакового диаметра, а исходное и завершающее события - двойными кружками. Работы показываются в соответствии с требованиями, описанными в разделе 2. При построении Сгр в полигональной форме допускается использовать наклонные линии с целью показа взаимосвязи между работами. Он получается более компактным, удобным для анализа взаимосвязей работ и расчета параметров, однако уступает в наглядности и удобстве для руководства спланированным ТЭП или для корректировки (оптимизации). После построения Сгр в полигональной форме (рис.1.6) рассчитываются основные временные параметры.

3

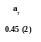
0.42

0.36

0.06

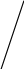
1

2

4

7

10

а₁₀

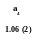
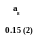
0.00

0.00

0.06

0.06

1.12

1.12

1.27

1.27

2.57

2.57

3.07

11

3.07

а₁₃

0.00

0.00

0.00

0.00

0.00

0.00

1.30 (4)

0.10(2)

5

6

8

9

а₁₂

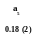
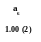
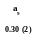
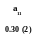
0.42

0.24

1.42

1.24

2.12

1.54

2.42

2.24

0.18

0.18

0.18

0.18

0.15 (2)

Рис. 1.6. Сгр ТО подвижной ДЭС, выполненный в полигональной форме

Основными параметрами сети являются ранние и поздние сроки наступления, а также резервы времени событий. Зная их, можно вычислить и другие параметры сети. Исходными данными для расчета основных параметров сети являются сведения о времени выполнения отдельных работ, которые указаны в таблице работ (см. рис.1.3). Проведем расчет основных временных параметров Сгр ТО подвижной ДЭС.

Ранний срок наступления j-го события t_р (j)

Ранее было отмечено, что событие может наступить только тогда, когда будут выполнены все работы, принадлежащие путям, идущим от исходного события к данному. Таким образом, оно не может наступить раньше окончания работ, принадлежащих самому длинному из предшествующих путей, и, следовательно, ранний срок наступления события численно равен продолжительности всей последовательности работ, составляющих этот путь, т.е.

. (1.2)

Данное выражение неудобно для практических расчетов, так как приходится всякий раз искать максимальный из путей, предшествующих i-му событию. Более удобной является следующая очевидная формула:

. (1.3)

Расчет значений ранних сроков наступления событий t_Р(i) ведется последовательно от исходного события до завершающего события (слева – направо) в порядке возрастания номеров событий. Ранний срок наступления исходного события равен нулю, а на Сгр при расчете временных параметров используют обозначение вида "00.00", которое соответствует: до точки – часам, после точки – минутам.

В качестве примера определим ранние сроки наступления событий Сгр, изображенного на рис. 1.6:

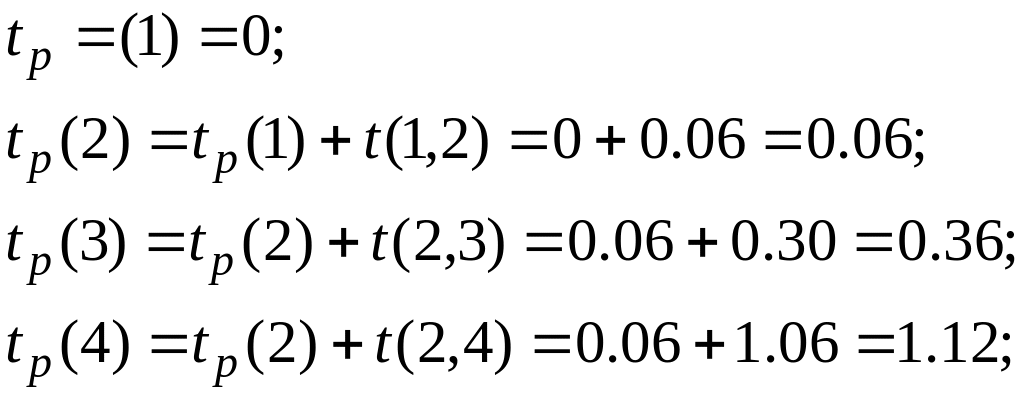
Рассчитанные значения t_Р(j) для событий Сгр записываются в левых частях соответствующих кружков.

Из соотношения (1.2) следует, что для завершающего события сети:

. (1.4)

Величину t_Р(С) назовем плановым сроком выполнения комплекса работ для принятой структуры Сгр. Плановый срок окончания комплекса работ t_Р(11)=3.07 является и поздним сроком наступления завершающего события для Сгр. Исходя из этого, определим поздние сроки наступления остальных событий.

Поздний срок наступления i-го события t_П(i)

Как было отмечено выше, некоторое событие i не может наступить раньше окончания работ, принадлежащих самому длинному из предшествующих этому событию пути. А допустимо ли наступление этого события позже определенного раннего срока его наступления? Допустимо, если более позднее наступление события не помешает своевременному плановому окончанию всего комплекса работ, отображаемого Сгр. Это будет иметь место в том случае, если путь максимальной продолжительности от i-го события до завершающего (последующий за i-м событием путь) меньше разности между плановым сроком окончания всего комплекса работ t_Р(С) и ранним сроком наступления i-го события, т.е.

. (1.5)

Например, для событий 7 и 9, изображенных на Сгр (см.рис.1.1), получаются значения:

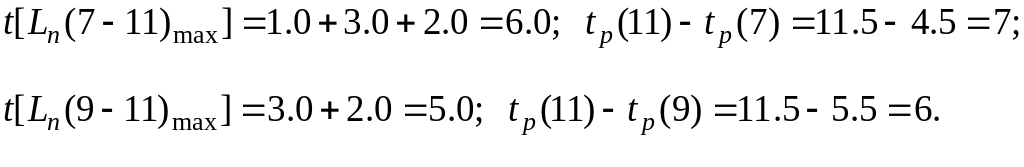
Отсюда следует, что событие 7 может наступить позже своего раннего срока наступления, а событие 9 – нет, так как оно не удовлетворяет соотношению (1.5).

Плановый срок окончания комплекса работ t_Р(с) обычно является и поздним сроком наступления завершающего события для детерминированных сетей, т.е.

. (1.6)

От неравенства (1.5) можно перейти к равенству, определяющему поздний срок наступления i-го события:

. (1.7)

Таким образом, поздний срок наступления события t_П(i) – это предельно допустимый срок, при котором у исполнителей еще остается время для выполнения к плановому сроку комплекса работ, следующих за данным событием.

Легко убедиться в том, что формула (1.7) неудобна для практического использования, так как вынуждает каждый раз искать максимальные пути, следующие за данным событием. Более удобным является следующее соотношение:

. (1.8)

Как следует из формулы (1.8), расчет поздних сроков наступления событий ведется последовательно от завершающего события к исходному (справа – налево) в порядке уменьшения номеров событий. Определим поздние сроки наступления событий Сгр, изображенного на рис. 1.6:

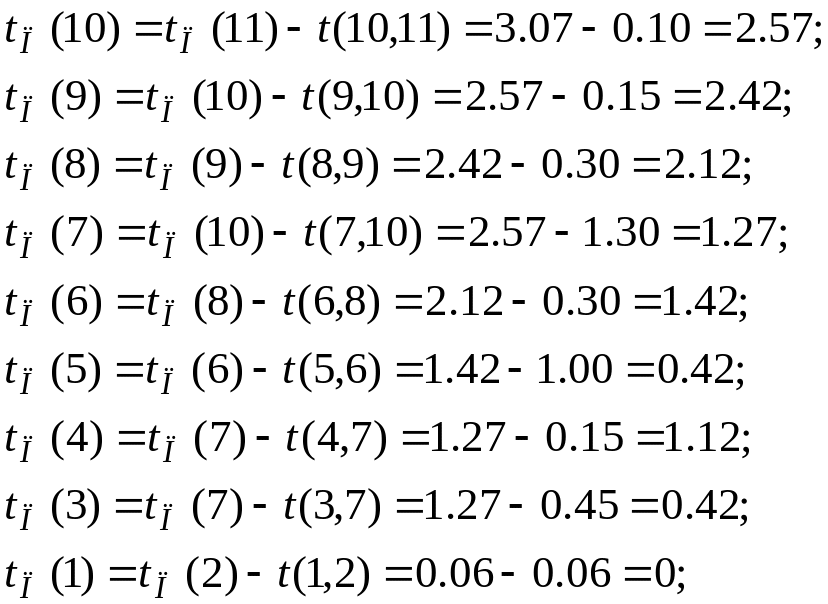
Р ассчитанные значения t_П(i) для событий Сгр записываются в правых частях соответствующих кружков.

Наличие поздних сроков наступления событий указывает на возможность задержек при выполнении отдельных работ. Например, событие "5" имеет поздний срок наступления, равный 0,42. Это событие наступит в свой поздний срок, если фактическая продолжительность предшествующей ему работы а₅ окажется равной 0,42 , вместо 0,18 по плану. Данная ситуация приведет к тому, что следующие за работой а₅ работы а₆, а₉, а₁₁, а₁₂ будут начинаться в поздние сроки наступления соответствующих событий, а продолжительность максимального пути, проходящего через событие 5 (1,2,5,6,8,9,10,11), станет равной продолжительности критического пути.

Таким образом, можно сделать вывод: если событие наступает в свой поздний срок, то максимальный путь, проходящий через это событие, становится критическим.

После определения поздних сроков наступления событий Сгр определяют резервы времени событий.

Резерв времени i-го события R(i)

Разность между поздним и ранним сроками наступления i-го события называют резервом времени события:

. (1.9)

Значения R(i) указывают в нижних частях кружков, обозначающих события.

Величина R(i) показывает, на какой предельно допустимый срок можно задержать наступление i-го события, не вызывая при этом увеличения продолжительности критического пути, т.е. увеличения продолжительности спланированного комплекса работ.

События, лежащие на критическом пути, не имеют резервов времени, так как для них t_Р(i)=t_П(i). В свою очередь, события, не принадлежащие критическому пути, имеют резервы времени событий. Определим для нашего примера резервы времени событий в соответствии с формулой (1.9):

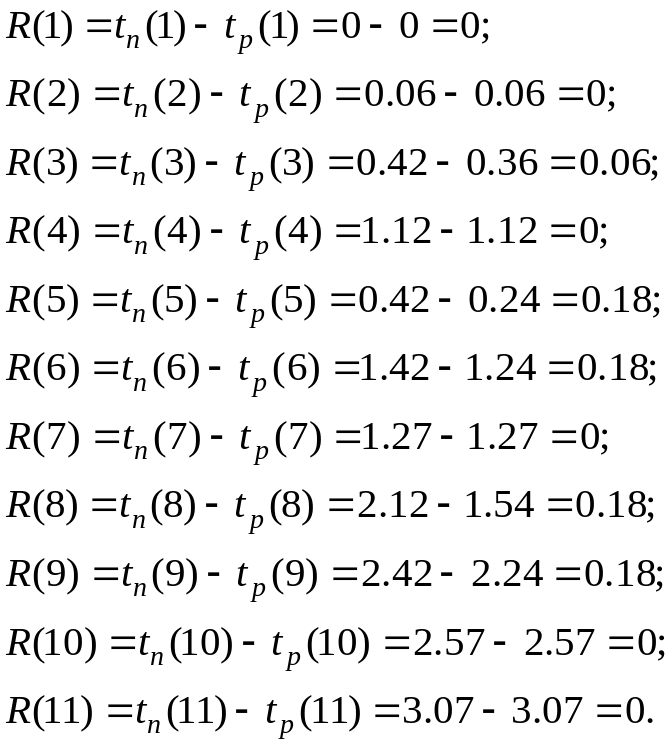
Рассчитанные значения t_Р(i), t_П(i), R(i) занесем в кружки Сгр, выполненного в полигональной форме (см. рис.1.6), обозначающие события, и в табл.1.2. Как известно, у событий, лежащих на критическом пути, значения резервов равны нулю. Используя этот признак, на Сгр, изображённом на рис. 1.6, утолщенной линией показан критический путь планируемого технологического процесса.

Таблица 1.2

№ события	Срок совершения события		Резерв времени события, R ( i )
	ранний, t p ( j )	поздний, t п ( i )
1 2 3 4 5 6 7 8 9 10 11	0 0.06 0.36 1.12 0.24 1.24 1.27 1.54 2.24 2.57 3.07	0 0.06 0.42 1.12 0.42 1.42 1.27 2.12 2.42 2.57 3.07	0 0 0.06 0 0.18 0.18 0 0.18 0.18 0 0

Рассчитанные параметры (табл.1.2) являются исходными данными для построения Сгр в ортогональной форме. Рассмотрим порядок построения Сгр в ортогональной форме.

IV этап. Построение Сгр в ортогональной форме с учетом продолжительности действительных работ и ожиданий и расчет дополнительных временных параметров.

Сгр в ортогональной форме можно строить с равномерной и неравномерной шкалой времени. Действительные работы и ожидания на таком графике изображаются горизонтальными линиями со стрелками, длина которых зависит от продолжительности работ. Фиктивные работы изображаются либо горизонтальными, либо вертикальными пунктирными линиями со стрелками. Кружки, обозначающие события, размешаются, как правило, против отметок времени, соответствующих ранним срокам наступления события, т.е. график строится по ранним срокам наступления событий.

Правила графического построения Сгр сводятся к следующим:

1. На отдельном листе бумаги в выбранном масштабе времени в нижней части проводится горизонтальная линия протяженностью, соответствующей директивному или предполагаемому времени завершения всего процесса. Линия делится на отрезки времени в часах. Масштаб выбирается таким образом, чтобы не было наложений событий друг на друга.

2. В левой части листа против начала отсчета времени двойным кружком изображается исходное событие.

3. От исходного до завершающего события работы изображаются отрезками прямых линий, параллельных оси времени со своими событиями.

4. Над линией, изображающей работу, подписывается код работы. Под линией подписывается продолжительность работы, в скобках указывается количество исполнителей.

5. Фиктивные работы (зависимость между событиями) могут изображаться пунктирной ориентированной линией со стрелкой или двумя касающимися кружками разного диаметра. Направление зависимости считается от большего кружка к меньшему. В кружке меньшего диаметра указывается номер последующего события для данной работы.

6. Работа, входящая в событие с резервом времени, изображается сплошной линией до «всплеска», соответствующего расчетной продолжительности работы, а далее изображается штрих - пунктирной ориентированной линией.

7. Если несколько работ имеют одно предшествующее или одно последующее событие, то факт начала или окончания работ показывается кружками меньшего диаметра. В кружках указываются номера соответствующих событий.

Для рассматриваемого нами примера Сгр в ортогональной форме представлен на рис.1.7.

Ниже Сгр в ортогональной форме строят график занятости (загрузки) личного состава (исполнителей), который наглядно показывает динамику задействования личного состава на разных этапах выполнения технологического процесса. Ось абсцисс соответствует временным интервалам выполнения работ Сгр. На оси ординат указывается количество исполнителей, одновременно задействованных (суммарное количество) на различных промежутках времени при выполнении всего цикла работ ТЭП.

Так при выполнении ТО подвижной ДЭС работу а₁ начинает выполнять один исполнитель, который задействован в течение 0,06 часов. Далее начинают одновременно выполнять работы (а₂, а₃, а₄, а₅) семь исполнителей в течение также 0,06 часов и т.д. Соответственно

работу а₁₃ заканчивает выполнять один исполнитель. В результате получается график занятости личного состава на различных интервалах времени в виде отдельных прямоугольников, вершины которого затем соединяются одной линией.

После построения Сгр в ортогональной форме и графика занятости личного состава (рис.1.7) проводится расчет дополнительных временных параметров. К дополнительным временным параметрам относятся: ранние и поздние сроки начала и окончания работ, а также полные и свободные резервы времени работ.

Ранние и поздние сроки начала и окончания работ рассчитываются по формулам:

t _p.н ( i , j ) = t _p ( i ) ; (1.10)

t _{p. o} ( i , j ) = t _p ( i ) + t ( i , j ) , i < j; (1.11)

t _{п. н} ( i , j ) = t _п ( j ) - t ( i , j ) , i < j; (1.12)

t _{п. о} ( i , j ) = t _п ( j ) . (1.13)

С учетом зависимостей (1.10) – (1.13) рассчитаем ранние и поздние сроки начала и окончания работ ТО подвижной ДЭС:

t_р.н.(а₁)=0 ; t_р.о.(а₁)=0.06 ;

t_р.н.(а₂)=0.06 ; t_р.о.(а₂)=0.12 ;

t_р.н.(а₃)=0.06 ; t_р.о.(а₃)=0.36 ;

t_р.н.(а₄)=0.06 ; t_р.о.(а₄)=1.12 ;

t_р.н.(а₅)=0.06 ; t_р.о.(а₅)=0.24 ;

t_р.н.(а₆)=0.24 ; t_р.о.(а₆)=1.24 ;

t_р.н.(а₇)=0.37 ; t_р.о.(а₇)=1.21 ;

t_р.н.(а₈)=1.12 ; t_р.о.(а₈)=1.27 ;

t_р.н.(а₉)=1.24 ; t_р.о.(а₉)=1.54 ;

t_р.н.(а₁₀)=1.27 ; t_р.о.(а₁₀)=2.57 ;

t_р.н.(а₁₁)=1.54 ; t_р.о.(а₁₁)=2.24 ;

t_р.н.(а₁₂)=2.24 ; t_р.о.(а₁₂)=2.39 ;

t_р.н.(а₁₃)=2.57 . t_р.о.(а₁₃)=3.07 .

Поздние сроки начала и окончания работ равны:

t_п.н.(а₁)=0 ; t_п.о.(а₁)=0.06 ;

t_п.н.(а₂)=2.51 ; t_п.о.(а₂)=2.57 ;

t_п.н.(а₃)=0.12 ; t_п.о.(а₃)=0.42 ;

t_п.н.(а₄)=0.06 ; t_п.о.(а₄)=1.12 ;

t_п.н.(а₅)=0.24 ; t_п.о.(а₅)=0.42 ;

t_п.н.(а₆)=0.42 ; t_п.о.(а₆)=1.42 ;

t_п.н.(а₇)=0.42 ; t_п.о.(а₇)=1.27 ;

t_п.н.(а₈)=1.12 ; t_п.о.(а₈)=1.27 ;

t_п.н.(а₉)=1.42 ; t_п.о.(а₉)=2.12 ;

t_п.н.(а₁₀)=1.27 ; t_п.о.(а₁₀)=2.57 ;

t_п.н.(а₁₁)=2.12 ; t_п.о.(а₁₁)=2.42 ;

t_п.н.(а₁₂)=2.42 ; t_п.о.(а₁₂)=2.57 ;

t_п.н.(а₁₃)=2.57 . t_п.о.(а₁₃)=3.07 .

Проведя анализ полученных результатов, можно сделать следующие выводы:

• ранние сроки начала работ равны ранним срокам свершения (наступления) их предшествующих событий;

• поздние сроки окончания работ равны ранним срокам свершения их последующих событий, за исключением работ а₂, а₇ и а₁₂, так как для событий 7, 10 рассчитывается путь максимальной продолжительности;

• для работ, лежащих на критическом пути ранние и поздние сроки начала и окончания работ равны ранним и поздним срокам свершения их предшествующих и последующих событий;

• поздний срок начала работ равен позднему сроку свершения их предшествующих событий, за исключением работы а₂, которая имеет значительный резерв времени для начала ее выполнения;

• поздний срок окончания работ равен позднему сроку свершения их последующих событий.

Резервами времени располагают не только события, но и пути (кроме критического), а также работы, не лежащие на критических путях. Вследствие того, что продолжительность критического пути больше продолжительности любого другого полного пути, образуется резерв времени каждого полного пути. Резерв времени пути распределяется на резервы временя работ, составляющих данный путь. Все эти работы одновременно не могут быть работами критического пути. Для характеристики резервов времени введено несколько параметров, из которых наиболее часто применяются в практике сетевого планирования такие, как полный и свободный резервы времени работ.

Полный резерв времени работы R_П(i,j)

Полный резерв времени работы показывает, насколько можно увеличить продолжительность отдельной работы или отсрочить ее начало, не изменяя при этом заданного срока окончания всего комплекса работ, и определяется по формуле:

. (1.14)

Если полный резерв времени выполнения одной из работ использовать полностью, то будут аннулированы полные резервы времени выполнения других последующих работ, принадлежащих пути максимальной длины, проходящему через эту работу. Резервы времени выполнения работ, лежащих на других путях (меньшей продолжительности), также проходящих через эту работу, сократятся и будут равны разности между прежним их резервом и использованным. Полный резерв времени выполнения каждой работы находится в распоряжении руководителя всего комплекса работ.

Свободный резерв времени работы Rс(i,j)

Свободный резерв времени работы показывает, насколько можно увеличить продолжительность отдельной работы или отсрочить ее начало, не изменяя при этом ранних сроков начала последующих работ, при условии, что начальное событие этой работы наступило в свой ранний срок, и определяется по формуле:

. (1.15)

Сравнивая соотношения (1.14) и (1.15), можно увидеть, что они отличаются только первым членом в правых частях равенств. Отсюда следует, что R_С(i,j) R_П(i,j), т.е. свободный резерв времени работы является частью ее полного резерва, а необходимым и достаточным условием принадлежности работы к критическому пути является равенство нулю ее полного резерва R_П(i,j)=0. Использование свободного времени выполнения какой-либо одной работы не изменяет величин свободных и полных резервов времени выполнения следующих за ней работ. Таким образом, свободный резерв времени выполнения работы может находиться в распоряжении непосредственного исполнителя этой работы.

В завершение вышесказанного определим полные и свободные резервы времени работ Сгр рассматриваемого ТЭП (см. рис.1.7), используемые в дальнейшем при анализе сети.

Расчет полных и свободных резервов времени работ:

На Сгр, выполненном в ортогональной форме (см. рис.1.7), достаточно просто определить работы, имеющие резервы времени. Так работы а₃, а₅, а₆, а₉, а₁₁ имеют только полные резервы, соответственно их свободные резервы равны нулю. Работы а₂, а₇, а₁₂ имеют и полные, и свободные резервы.

Для удобства проведения анализа Сгр полученные результаты занесем в табл. 1.3.

Таблица 1.3

Код работы a i	Сроки совершения работ				Резервы времени работ
	ранние		поздние
	t p.н(i, j )	t p. o(i, j)	t п.н(i , j)	t п.о (i ,j)	полный R п (i , j)	cвободный R c (i , j)
а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11 а12 а13	0 0.06 0.06 0.06 0.06 0.24 0.37 1.12 1.24 1.27 1.54 2.24 2.57	0.06 0.12 0.36 1.12 0.24 1.24 1.21 1.27 1.54 2.57 2.24 2.39 3.07	0 2.51 0.12 0.06 0.24 0.42 0.42 1.12 1.42 1.27 2.12 2.42 2.57	0.06 2.57 0.42 1.12 0.42 1.42 1.27 1.27 2.12 2.57 2.42 2.57 3.07	0 2.45 0.06 0 0.18 0.18 0.06 0 0.18 0 0.18 0.18 0	0 2.45 0 0 0 0 0.06 0 0 0 0 0.18 0

Анализируя результаты расчетов (табл.1.3), можно сделать ряд выводов, подтверждающих теоретические положения:

1) полные и свободные резервы времени работ, лежащих на критическом пути, равны нулю;

2) работы, не лежащие на критическом пути и не имеющие параллельных работ и не являющиеся последними на участке, не совпадающем с критическим путем, имеют только полные резервы времени, а их свободные резервы времени равны нулю.

Опыт подсказывает, что для того, чтобы избежать ошибки при расчете резервов времени работ, удобнее пользоваться ортогональной формой Сгр.

С нанесением на Сгр необходимых обозначений завершается его разработка. Далее проводится анализ Сгр и проверка правильности его построения.

Рассмотрим содержание V этапа построения Сгр.

V этап. Анализ Сгр и проверка правильности его построения.

Проверка правильности построения Сгр выполняется в соответствии с правилами, изложенными при рассмотрении этапов II и IV. При необходимости проводится его корректировка.

Анализ Сгр производится на основе расчетов и дополнительных графических построений. На основе анализа Сгр делают вывод о пригодности составленного плана работ заданным критериям, о необходимости его корректировки и оптимизации. Накопленный опыт использования сетевых моделей для планирования технологических процессов, проводимых на ВВТ, позволяет выделить несколько направлений, по которым следует проводить анализ Сгр:

1. Определение работ ТЭП, принадлежащих критическому пути, и графическое построение критического пути. Исходными данными для этого служат рассчитанные по формулам (1.3, 1.8 – 1.15) резервы времени событий и работ.

Для нашего примера работы а₁, а₄, а₈, а₁₀, а₁₃ лежат на критическом пути (являются критическими работами), поэтому на рис.1.7 двойными линиями покажем критический путь, проходящий через эти работы.

2. Сравнение продолжительности критического пути с директивно установленным временем на проведение данного комплекса работ.

Исходя из словесного описания ТЭП, директивное время на выполнение всего цикла работ ТО подвижной ДЭС составляет 3 часа. Однако при планировании ТЭП мы на 7 минут превысили директивно установленное время. Следовательно, разработанный нами Сгр (рис.1.7) является неоптимальным, и в дальнейшем необходимо провести его оптимизацию.

3. Сравнение количества личного состава, необходимого для выполнения комплекса работ ТЭП в соответствии с Сгр и выделяемого на эти работы. С этой целью ниже Сгр в ортогональной форме построен (см. рис.1.7) график занятости (загрузки) личного состава (исполнителей), по которому рассчитывается коэффициент занятости личного состава К_З. Данный коэффициент оценивает степень использования людских ресурсов при выполнении заданного минимума paбoт, отображаемого Сгр, и определяется в соответствии с формулой:

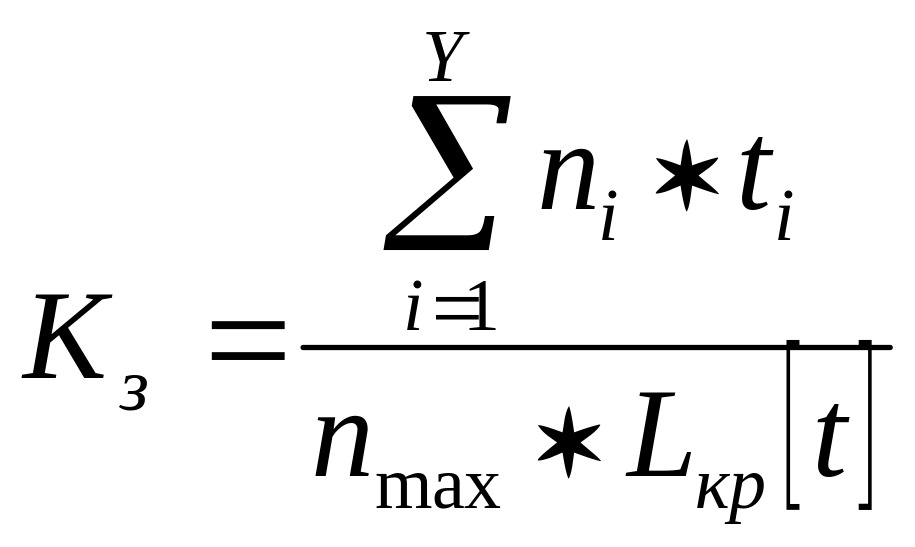, (1.16)

где n_i.- количество исполнителей; занятых на i-м интервале; t_i – продолжительность i-го интервала; n_max – наибольшее число исполнителей, занятых одновременно при выполнении работ Сгр; Y– количество интервалов.

Рассчитаем Кз для графика занятости личного состава, представленного на рис.1.7:

.

В данном примере в числителе находится сумма слагаемых, в каждом из которых первый сомножитель указывает на количество исполнителей, участвующих в проведении работ на интервале t_i, а второй – на продолжительность интервала t_i в минутах, в знаменателе – произведение, первый сомножитель которого равен максимальному числу исполнителей, задействованных при выполнении работ одновременно, а второй сомножитель – продолжительности критического пути в минутах. О характере загрузки исполнителей судят по очертанию графика занятости или по величине коэффициента Кз.

На графике занятости личного состава (см. рис.1.7) резко выделяются некоторые участки по высоте. Это свидетельствует о неудачном планировании ТЭП, с точки зрения использования исполнителей. В идеале стремятся к такому задействованию личного состава, чтобы ему соответствовал прямоугольный график его занятости с К₃=1.

Рассчитанный нами коэффициент занятости равен Кз=0.71, следовательно, при планировании ТО подвижной ДЭС мы недостаточно полно использовали имеющиеся силы и средства.

4. Расчет коэффициента напряженности работ К_Н(i,j).

Данный коэффициент характеризует напряженность плановых сроков выполнения работы. Он определяется простой формулой:

(1.17)

где - продолжительность участков критического пути, совпадающих с путем максимальной продолжительности, проходящим через работу ( i , j ) .

Следует иметь в виду, что для работ, лежащих на критическом пути, коэффициенты напряженности работ К_Н(i,j) всегда равны единице, так как резервы R_П(i,j)=0. Для рассматриваемого Сгр (см. рис. 1.7) этими работами являются: а₁, а₄, а₈, а₁₀, а₁₃. Для остальных работ коэффициент напряженности равен:

,

где 165 – полный резерв времени работы (а₂) в минутах; 187 – продолжительность критического пути в минутах; 6+10 – продолжительность участков критического пути в минутах (между событиями 1,2 и 10,11), совпадающих с путем максимальной продолжительности, проходящим через работу (а₂);

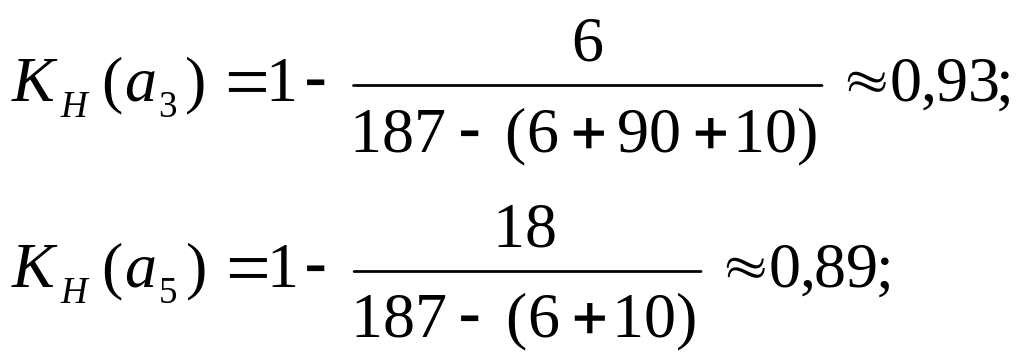
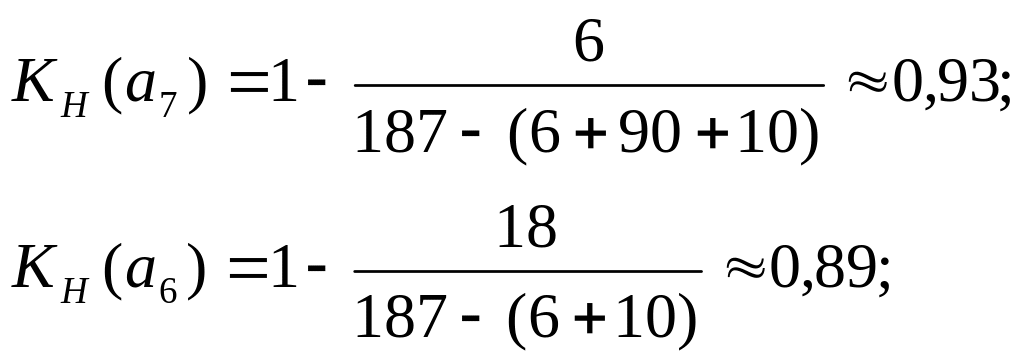
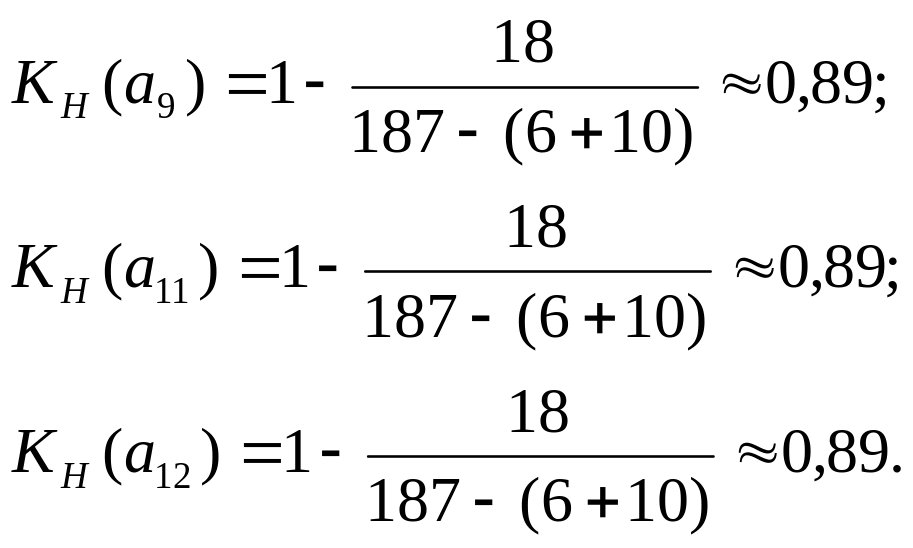
Из анализа полученных числовых результатов можно сделать вывод, что для работ одного "яруса" Сгр, между общими начальными и конечными событиями этой группы работ, коэффициент напряженности работ одинаков. Напряженность работ, входящих в Сгр, условно распределяют на три зоны:

• критическую зону, к которой относятся работы с К_Н(i,j)=0,8...1,0;

• промежуточную зону, к которой относятся работы с К_Н(i,j), лежащим в пределах от 0,5 до 0,8;

• зону резервов, к которой относятся работы с К_Н(i,j)<0,5.

Чтобы определить, к какой из зон относятся рассчитанные в примерах коэффициенты напряженности работ Сгр К_Н(i,j), результаты расчетов запишем в табл. 1.4.

Таблица 1.4

Код работы a i	КН ( i , j )	Зона
		критическая 0.8 < КН ≤ 1.0	промежуточная 0.5 < КН ≤ 0.8	резервов КН ≤ 0.5
а1 а2 а3 а4 а5 а6 а7 а8 а9 а10 а11	1 0.04 0.93 1 0.89 0.89 0.93 1 0.89 1 0.89	+ + + + + + + + + +		+

Продолжение табл.1.4

Код работы аi	Кн (i, j )	Зона
		критическая 0.8 < Кн ≤ 1.0	промежуточная 0.5 < Кн ≤ 0.8	резервов Кн ≤ 0.5
а12 а13	0.89 1	+ +

Из табл. 1.4 можно сделать следующий вывод:все работы, за исключением работы а₂, относятся к критической зоне. Следовательно,

чем ближе работа к критической зоне, тем больше требований должно предъявляться к организации труда исполнителей и контролю их деятельности.

По результатам анализа сетевого графика делается вывод о проведенном планировании ТЭП. Качественно и в полном объеме проведенный анализ Сгр, а при необходимости его корректировка служат реальной базой для успешного выполнения заданного технологического процесса в установленный срок. Иначе говоря, создаваемые планы по реализации ТЭП должны быть оптимальными в соответствии с некоторыми признаками, которые называют критериями оптимальности.

Анализ разработанного Сгр (см. рис.1.7) показал, что он не удовлетворяет директивному времени выполнения всего комплекса работ. В связи с этим возникает необходимость проведения его оптимизации.