2. Основные понятия и определения Сгр

Сгр (сеть) есть графическое изображение процесса выполнения некоторой совокупности работ, наглядно отражающее взаимосвязь и технологическую последовательность.

Основными понятиями сетевого планирования являются: работа, событие, путь.

Термин "работа" может иметь следующие значения:

действительная работа – трудовой процесс, требующий затрат времени, труда и ресурсов (например, смазка агрегата, проверка состояния и наличия ЗИП и т.д.);

ожидание – процесс, не требующий затрат труда, но занимающий определенное время (например, остывание аппаратуры, высыхание краски и т.д.);

фиктивная работа или зависимость – логическая связь между работами, не требующая затрат времени и ресурсов, но указывающая, что возможность начала одной работы (или нескольких) непосредственно зависит от результатов другой (других) (например, совместные испытания агрегатов не могут быть начаты до окончания автономных проверок агрегатов, участвующих в этих испытаниях).

Действительные работы и ожидания изображаются на графиках сплошными линиями со стрелками. Над стрелкой действительной работы, как правило, подписывается содержание работы или ее код (шифр), а под ней указывается документ, либо пункт документа, либо технологическая карта (ТК) документа, по которым выполняется данная работа, продолжительность работы и в скобках количество исполнителей. Под стрелкой ожидания обычно указывается время ожидания, а сверху стрелки может быть написано "Ожидание". Пример изображения действительной работы показан на рис. 1.1.

Фиктивные работы на Сгр изображаются в виде пунктирных линий со стрелками либо двумя соприкасающимися кружками разных размеров, при этом направление зависимости установлено от большого круга к маленькому. В полигональной форме Сгр используется первый способ изображения фиктивной работы, т.е.

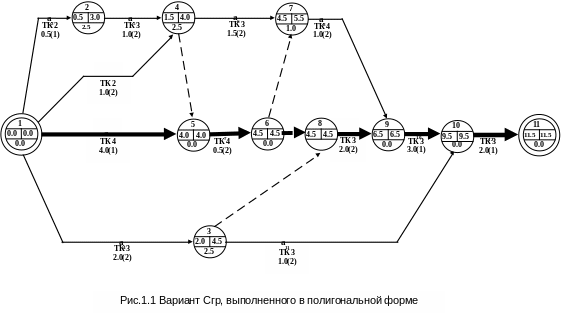
пунктирной линией со стрелкой, а в ортогональной - второй. На

рис. 1.1 фиктивными работами являются работы, заключенные между кружками 4 и 5, 6 и 7, 6 и 8, 3 и 8.

Каждая работа сети начинается и кончается событием, т.е. имеет начальное i и конечное j события и кодируется номерами этих событий. Например, фиктивная работа 4, 5, где 4 – начальное событие, а 5 – конечное событие.

Событие есть момент (факт) начала или окончания работы. Оно не имеет длительности. Событие наступает только тогда, когда выполнены все предшествующие этому событию работы. Наступление события является обязательным условием для начала следующих за ним работ. Событие, которое не имеет предшествующих работ, называется исходным событием, а событие, не имеющее последующих работ, – завершающим событием.

События изображаются кружками, исходное и завершающее события – двойными кружками. В ряде случаев удобно для увеличения наглядности в одном Сгр равные по характеристикам события изображать различными геометрическими фигурами. В практике планирования эксплуатации вооружения, как правило, используется изображение событий кружками. Внутри кружка (рис. 1.1), разделенного определенный образом, записываются вверху–номер события, внизу– резерв времени события, в середине слева – ранний срок наступления события, справа – поздний срок наступления события. События, являющиеся начальными или конечными сразу для нескольких работ, изображаются кружками разных размеров с одинаковыми номерами, один из которых большего диаметра. В большом кружке записываются все параметры события, отмеченные выше, а в маленьком – только номер события, соответствующий большому кружку.

Путем Сгр называется любая последовательность работ, в которой конечное событие одной работы является начальным для другой. Различают пути трех основных видов:

путь от исходного события до i-го события называется путем предшествующим i-му событию и обозначается как [L_n(J-i)] (например, на рис. 1.1 предшествующие пути 8-му, событию пути, проходящие через события 1,2,4,5,6,8 или 1,5,6,8 или 1,3,8, или 1,4,5,6,8);

путь от i-го события до завершающего события называется путем, последующим за данным событием, и обозначается как

[L_n(i-C)] (например, на рис. 1.1 путь последующий за 6-м событием есть путь, проходящий через события 6,7,9,10,11 или 6,8,9,10,11);

путь от исходного до завершающего события называется полным путем и обозначается как [L_n(J-C)] (например, для Сгр, изображенного на рис. 1.1, полными являются пути, проходящие через события: 1,2,4,7,9,10,11; 1,4,7,9,10,11; 1,4,5,6,7,9,10,11; 1,4,5,6,8,9,10,11; 1,5,6,8,9,10,11; 1,5,6,7,9,10,11; 1,3,10,11; 1,3,8,9,10,11).

Как видно из приведенного примера, в сети может быть несколько полных путей, и одна и та же работа может принадлежать нескольким путям. Продолжительность пути равна сумме продолжительностей составляющих его работ.

Полный путь максимальной продолжительности называется критическим путем и обозначается как [L_кр]. В сети может быть несколько критических путей (в принципе, количество критических путей может быть равно числу полных путей), которые изображаются либо утолщенными, либо двойными линиями, либо выделяются цветом. На Сгр (см. рис. 1.1) критическим путем является путь, проходящий через события 1,5,6,8,9,10,11.

Работы, лежащие на критическом пути, называются критическими.

Сгр можно классифицировать по разным признакам. Например, по форме представления сети они могут быть ортогональными и полигональными. Сгр в полигональной форме (см. рис. 1.1) получается более компактным, удобным для анализа взаимосвязей работ и расчета параметров, однако уступает в наглядности и удобстве для руководства спланированным ТЭП или для корректировки (оптимизации) сети по сравнению с графиком в ортогональной форме (рис. 1.2). Сгр в ортогональной форме можно строить с равномерной и неравномерной шкалой времени. Действительные работы и ожидания на таком графике изображаются горизонтальными линиями со стрелками, длина которых зависит от продолжительности работ. Фиктивные работы изображаются либо горизонтальными, либо наклонными (вертикальными) пунктирными линиями со стрелками. Кружки, обозначающие события, размешаются, как правило, против отметок времени, соответствующих ранним срокам наступления события, т.е. график строится по ранним срокам наступления событий.

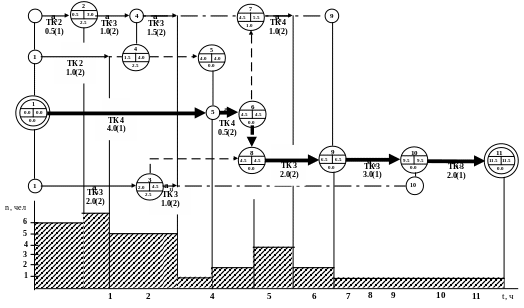
Рис.1.2. Вариант Сгр, выполненного в ортогональной форме

и графика занятости личного состава

Данное практическое занятие посвящено решению задачи по разработке Сгр ТЭП (отработке методики решения задач) в соответствии с заданными исходными данными.