2.4.3. Продольное ребро.

Подбор арматуры продольного ребра выполняем как для изгибаемого элемента таврового профиля высотой h = 400 мм и фактической шириной b_f = 1445 мм.

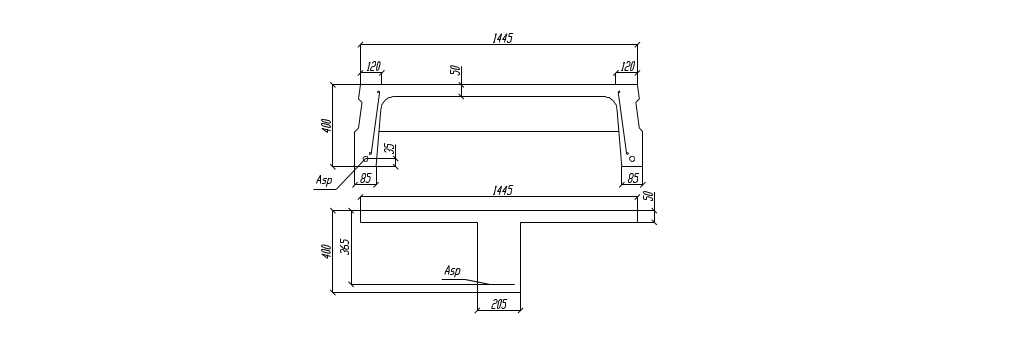
Рис. 2.10. Фактическое сечение продольного ребра.

Средняя ширина ребра:

Определим значение

_{Принимаем значение, вводимое в расчет .}

Арматура класса А1000; (R_s = 830 МПа).

Зададимся величиной предварительного напряжения. Для стержневой арматуры: . Примем:

где - нормативное сопротивление растяжению арматуры, R_sn = 1000 МПа (согласно табл.7.[2]).

С учетом потерь:

Согласно п.3.1.2.2[2], расчет по прочности нормальных сечений производят в зависимости от соотношения между значением относительной высоты сжатой зоны бетона , определяемой из соответствующих условий равновесия, и значением граничной относительной высоты сжатой зоны , при которой предельное состояние элемента наступает одновременно с достижением в растянутой арматуре напряжения, равного расчетному сопротивлению .

Значение определяют по формуле

,

где - относительная деформация арматуры растянутой зоны, вызванная внешней нагрузкой при достижении в этой арматуре напряжения, равного ;

- относительная деформация сжатого бетона при напряжениях, равных , принимаемая равной 0,0035.

Для арматуры с условным пределом текучести значение определяют по формуле

,

где - предварительное напряжение в арматуре с учетом всех потерь и =0,9;

согласно табл.8 [2].

Получим:

Определяем высоту рабочей зоны бетона по формуле

h ₀ = 400 – 35 = 365 мм

Проверяем положение нейтральной оси, проверяем условие, принимая A_s^/=0

т.е. нейтральная ось проходит в полке, и расчет производим как для прямоугольного сечения шириной = = 144,5 см.

Вычисляем значение α_m по формуле

Сжатая арматура не требуется.

Требуемую площадь сечения растянутой преднапряженной арматуры определяем по формуле

Для определения диаметра арматуры при известном ее классе, определим коэффициент работы высокопрочной арматуры при напряжениях выше предела текучести, .

где для арматуры класса А1000.

При можно принимать .

. Принимаем .

_{Окончательно определим площадь арматуры}

Принимаем 2Ø16 А1000 (A_sp = 4,02 см²).

В верхней и нижней зонах продольных ребер для обеспечение плоского каркаса конструктивно установим два стержня Ø 10 А240.

Рис. 2.11. Армирование продольного ребра.

2.5. Расчет элементов плиты по наклонным сечениям.

2.5.1. Расчет поперечного ребра.

2.5.1.1. Расчет по наклонным трещинам на действие поперечной силы.

Рис.2.12. Расчетная схема и эпюра изгибающего момента поперечного ребра.

Определим эквивалентную нагрузку, действующую на поперечное ребро. Для этого определим расчетные нагрузки, действующие на наклонные сечения.

где – эквивалентная временная нагрузка.

Эквивалентность достигается по моменту в середине пролета

Определим, нужно ли устанавливать поперечную арматуру по расчету, для этого необходимо проверить выполнение следующих условий:

где Q_max – перерезывающая сила на опоре,

R_bt – прочность бетона на растяжение, для бетона В40: ;

Q – перерезывающая сила на расстоянии с от опоры.

Одно условие выполнилось, проверим выполнение другого. Для этого необходимо определить величину с.

с принимается не более:

Проверим выполнение этих условий:

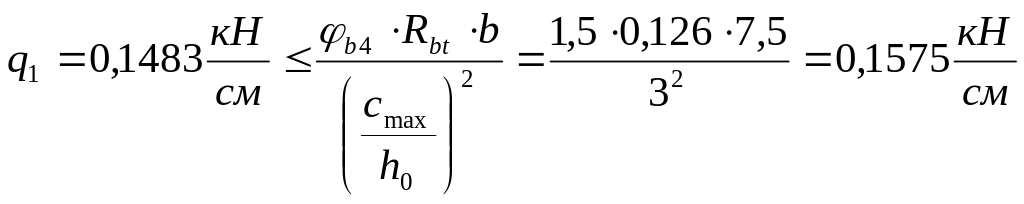
Следовательно, с принимаем равным:

Условия выполняются, т.е. поперечная арматура по расчету не требуется. Т.к. высота балки более150 мм поперечную арматуру необходимо установить конструктивно.

Зададимся шагом поперечной арматуры

Примем шаг поперечной арматуры равным S=100 мм. Арматуру по всей длине поперечного ребра устанавливаем с шагом S=100 мм.

Из условия свариваемости при диаметре продольной арматуры Ø6 А1000 определим наименьший допустимый диаметр поперечной арматуры 3 мм. Примем арматуру Ø 3 В500.

Рис. 2.13. Армирование поперечного ребра.

Рис. 2.14. Армирование поперечного ребра.