2.4. Регрессионные статистические характеристики сигналов и помех в автономных информационных системах

Регрессионные статистические характеристики сигналов и по­мех в АИС ближней локации могут быть получены на основании тео­ретических исследований обоснованных математических моделей и последующей проверкой адекватности этих моделей путем экспе­риментальных исследований реальных сигналов и помех.

В некоторых случаях матрица корреляционных моментов мо­жет быть получена только в результате эксперимента. Точно опре­делить моменты случайных величин по выборочным данным невоз­можно. По выборке ограниченного объема можно найти лишь оценки интересующих параметров.

Рассматривается вопрос о точности оценок параметров для не­прерывных реализации нецентрированных процессов на интерва­ле , в общем случае этот интервал меньше или равен интервалу наблюдения.

Специфика работы систем ближней локации требует, чтобы статистические характеристики были получены по каждой выбо­рочной реализации. Действительно, на каждой траектории на вход системы ближней локации поступает одна реализация х(t), кото­рую удобно характеризовать математической моделью вида

,

где f – детерминированная функция времени t, векторной слу­чайной величины и и векторной случайной реализации , за­висимых от параметров условий встречи и условий применения.

В некоторых случаях при моделировании сигналов можно рас­сматривать модель, в которой сигнал является векторной случай­ной величиной (когда m>>1). Случайные величины также зависят от параметров условий встречи и условий применения.

Для анализа работы систем ближней локации на каждой траек­тории необходимо знание статистических характеристик отдельной реализации, а не характеристик, усредненных по всему множеству сигналов.

Пусть выборочная реализация сигнала в доплеровской системе ближней локации представляет собой узкополосный стационарный в широком смысле случайный процесс и имеет нормированную автокорреляционную функцию (АКФ) (рис.2.2, а)

.

На другой траектории при отличных от первых условиях встре­чи и относительной скорости сигнал будет иметь АКФ (рис.2.2, б)

,

отличающуюся от АКФ (3.40) параметрами a и . Из рис.2.2 видно, что отсчеты доплеровского сигнала каждой реализации, от­стоящие на , для узкополосного процесса имеют нормирован­ный коэффициент корреляции, близкий к –1.

Рис. 2.2. Нормированные автокорреляционные функции узкополосных (а, б) и широкополосного процессов (в)

Нормированная АКФ ансамбля реализаций, отличающих­ся значением доплеровской частоты от до , имеет вид, пока­занный на рис. 2.2, в.

Аналогичную АКФ имеет шум с полосой . В нормиро­ванной АКФ ансамбля реализации отсутствует коррелированность с отсчетов сигнала, отстоящих на половину сред­него периода колебаний. Из этого следует, что при статистической обработке сигналов по ансамблю теряется информация об узкополосности каждой выборочной реализации, т. е. целесообразно по­лучать статистические характеристики каждой выборочной реали­зации.

В общем случае сигналы и помехи на входе систем ближней локации –нестационарные случайные процессы. Статистические характеристики нестационарных процессов должны получаться лишь усреднением по ансамблю. Разрешить столь противоречивые требования можно, если выбрать статистические характеристики, которые отражают информативные признаки объектов на каждой выборочной реализации, усреднением на интервале времени Т. Та­кими статистическими характеристиками применительно к систе­мам ближней локации являются вззимо - и авторегрессионные функции, оценки которых могут быть получены через оценки на­чальных моментов.

Так, оценки взаимокорреляционной функции и среднего значе­ния квадрата можно записать в виде:

, (2.40)

.

В формуле (2.40) Т – фиксированный интервал интегрирова­ния, так как предполагается, что процессы заданы на интервале .

На основании выражений (2.22) и (2.35) оценка взаиморегрес­сионной функции случайных процессов может быть

.

Оценки автокорреляционной и авторегрессионной функций яв­ляются частным случаем оценок взаимокорреляционной и взаимо­регрессионной функций, когда обе реализации х(t) и у(t) совла­дают:

;

;

.

В некоторых случаях процессы нестационарны за счет измене­ния во времени математических ожиданий и , среднеквадратических значений и , причем математические ожидания могут быть рассчитаны. В этих случаях на основании выражений (2.22) и (2.35 ) взаиморегрессионная функция может быть определена как

,

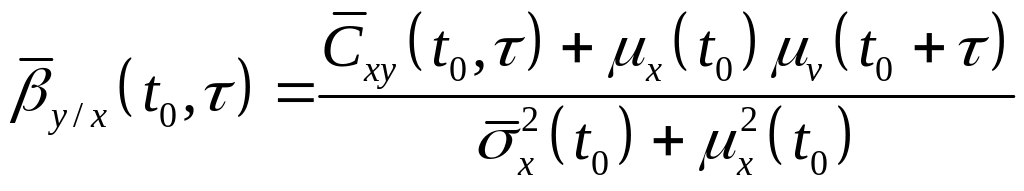где

;

.

В некоторых случаях величина также может быть рассчи­тана, тогда в эксперименте определяют нормированную взаимокорреляционную функцию , причем может оказаться, что норми­рованный центрированный случайный процесс стационарен. Тогда

.

При обработке реализации сигналов на ЭВМ исходный непре­рывный сигнал должен быть представлен в виде дискретного вре­менного ряда, для этого можно воспользоваться дискретизацией выборочных реализации по Котельникову.

Рис. 2.3. Формирование выборки объемом (N+1) из реализации