1. Проекции плоскостей уровня

Плоскостями уровня называются плоскости, параллельные плоскостям проекций.

Характерная особенность этих плоскостей состоит в том, что элементы, расположенные в этих плоскостях, проецируются на соответствующую плоскость проекций в натуральную величину.

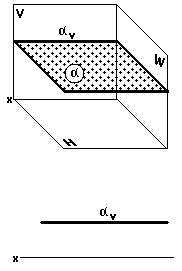
Горизонтальная плоскость (рис. 30)

Горизонтальная плоскость параллельна горизонтальной плоскости проекций.

На двухкартинном комплексном чертеже она изображается одним фронтальным следом, параллельным оси x.

На рис. 30 изображена горизонтальная плоскость (_V).

Фронтальная плоскость (рис. 31)

Фронтальная плоскость параллельна фронтальной плоскости проекций.

На двухкартинном комплексном чертеже она изображается одним горизонтальным следом, параллельным оси x.

На рис.31 изображена фронтальная плоскость (_).

Рис. 30 Рис. 31

Профильная плоскость (рис. 32)

Профильная плоскость параллельна профильной плоскости проекций.

На двухкартинном комплексном чертеже она изображается двумя следами: горизонтальным и фронтальным, перпендикулярными оси x.

На рис.32 изображена профильная плоскость (_H,V).

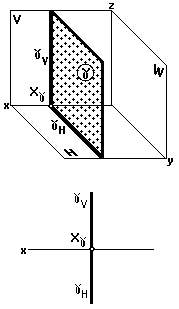
2. Рис. 32

   Проекции проецирующих плоскостей

ПРОЕЦИРУЮЩИМИ называются плоскости, перпендикулярные к плоскостям проекций.

Характерной особенностью таких плоскостей является их собирательное свойство. Оно заключается в следующем: соответствующий след — проекция плоскости — собирает одноименные проекции всех элементов, расположенных в данной плоскости.

Горизонтально-проецирующая плоскость (рис. 33)

Горизонтально-проецирующая плоскость перпендикулярна к горизонтальной плоскости проекций H.

Рис. 33 Рис. 34

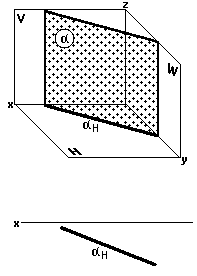
Горизонтальные проекции всех точек, принадлежащих горизонтально-проецирующей плоскости , располагаются на горизонтальном следе — проекции_Hэтой плоскости (рис. 33).

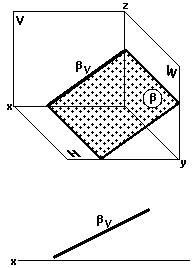
Фронтально-проецирующая плоскость (рис. 34)

Фронтально-проецирующая плоскость перпендикулярна к фронтальной плоскости проекций V.

Фронтальные проекции всех точек, принадлежащих фронтально-проецирующей плоскости , располагаются на фронтальном следе — проекции_этой плоскости (рис. 34).

Профильно-проецирующая плоскость (рис. 35)

Профильно-проецирующая плоскость перпендикулярна к профильной плоскости проекций W.

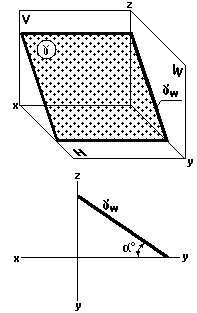
Рис. 35

Профильные проекции всех точек, принадлежащих профильно-проецирующей плоскости , располагаются на профильном следе — проекции этой_Wплоскости (рис. 35).

3. Взаимное расположение двух плоскостей

Две плоскости могут быть параллельными или пересекаться между собой.

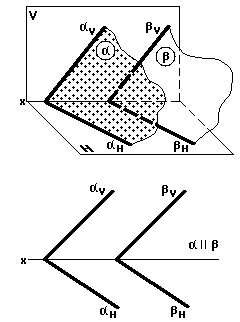
Параллельные плоскости (рис. 36)

Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. В качестве пересекающихся прямых в каждой из двух параллельных плоскостей можно взять их следы.

На рис. 36 изображены две взаимно параллельные плоскости и, которые на комплексном чертеже заданы следами_Vи_H, и_V,_H.

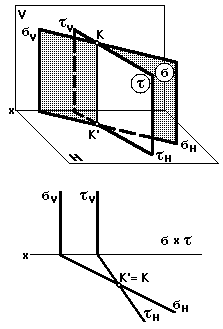
Пересекающиеся плоскости (рис. 37)

На рисунке изображены пересекающиеся плоскости и.

Рис. 36 Рис. 37

Пересечение плоскостей подтверждается пересечением пары их одноименных следов (точка К=К').