7. Условие видимости на чертеже

Для большей наглядности невидимые части предмета вычерчивают штриховыми линиями (либо совсем не вычерчивают).

Вопрос о видимости решают путем сравнения координат YилиZточек, лежащих на одном проецирующем луче.

Точки, лежащие на одном проецирующем луче, называются КОНКУРИРУЮЩИМИ.

Принято считать, что из двух конкурирующих точек на горизонтальной проекции видна та точка, координата Zкоторой больше, а на фронтальной проекции — координатаYкоторой больше.

Из рис. 57 легко установить, что на горизонтальной проекции из двух точек С и Dвидимой будет точкаC(C'), а на фронтальной проекции из двух точекAиBбудет видимой точкаB(B'').

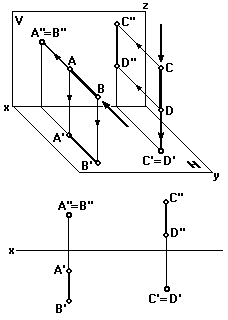
Рис. 57

Определим видимость на рис.55.

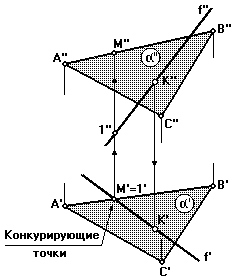
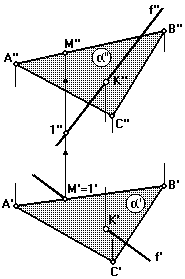
а) Для определения видимости прямой f на ГОРИЗОНТАЛЬНОЙ проекции рассмотрим две произвольные конкурирующие точки, например точки 1' и М'(точка 1 принадлежит прямой f, а точка М — отрезкуАВ) (рис. 58).

Координата ZточкиМбольше, следовательно на горизонтальной проекции прямая f на участке от точки 1 до точкиКрасположена ниже плоскости и является невидимой (рис.59).

Рис. 58 Рис. 59

б) Для определения видимости прямой f на ФРОНТАЛЬНОЙ проекции рассмотрим две другие конкурирующие точки, например точки 2'' и Е''(точка 2 принадлежит прямой f, а точкаЕ— отрезкуАВ) (рис. 60).

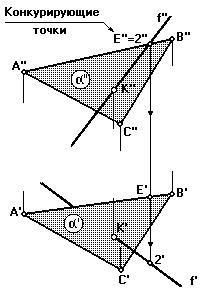
Координата Yточки 2 больше, следовательно на фронтальной проекции прямая f на участке от точкиKдо точки 2 расположена перед плоскостью и является видимой (рис.  61).

Рис. 60 Рис. 61

6. Перпендикулярность геометрических элементов

План:

6.1. Главные линии плоскости

6.2. Прямая, перпендикулярная к плоскости

6.3. Перпендикулярные плоскости

6.4. Перпендикулярные прямые

1. Главные линии плоскости

Кроме прямых линий общего положения, в плоскости отмечают три главные линии: горизонтальную (горизонталь), фронтальную (фронталь) и линию наибольшего наклона. Эти линии применяют как вспомогательные: они упрощают решение задач. Две из них — горизонтальная и фронтальная — уже рассматривались.

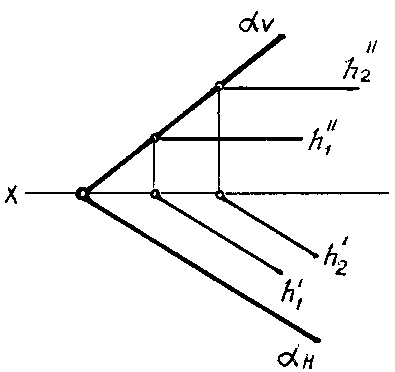
*Необходимо добавить, что все горизонтальные линии плоскости параллельны между собой, а их горизонтальные проекции параллельны горизонтальному следу плоскости (рис. 62). Горизонтальный след плоскости — одна из горизонталей.

*Все фронтальные линии плоскости параллельны между собой, а их фронтальные проекции параллельны фронтальному следу плоскости. Фронтальный след плоскости — одна из фронтальных линий (рис. 63).

Рис. 62 Рис. 63

Линии наибольшего наклона плоскости

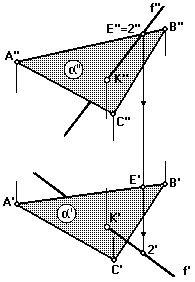
Прямую, лежащую в плоскости и имеющую наибольший угол с той или друго плоскостью проекций, называют линиейнаибольшегонаклона (ЛНН).

Линии наибольшего наклона плоскости перпендикулярны к ее следам или к линиям уровня (либо к ее горизонталям, либо к фронталям, либо к ее профильным прямым) (рис. 64).

В случае перпендикулярности к горизонтали определяется наклон к плоскости проекций H (при этом ЛНН называют линией наибольшего ската), перпендикулярности к фронтали — наклон к плоскости проекций V, перпендикулярности к профильной прямой — наклон к плоскости проекций W.

Рис. 64

На рис. 65, 66 дано изображение плоскости (аb), для которой требуется построить линию наибольшего наклона к горизонтальной плоскости проекций H.

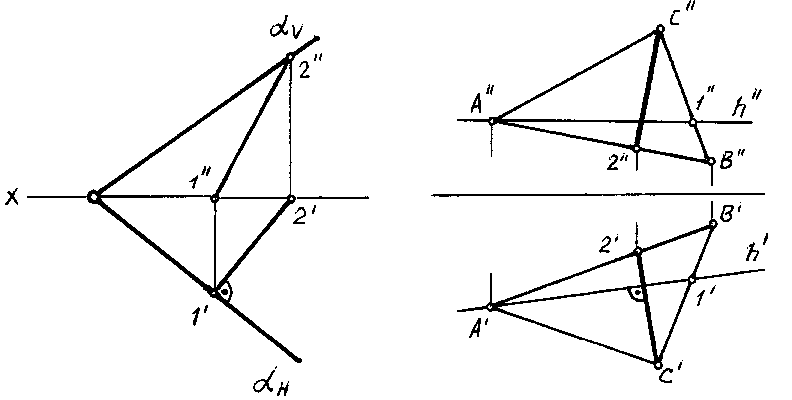
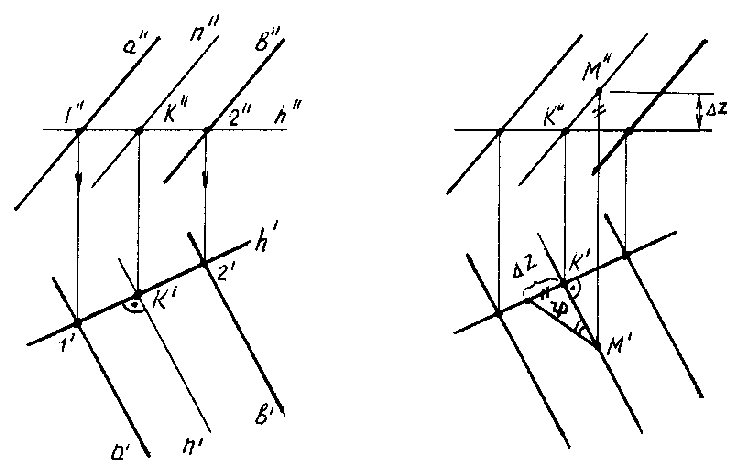
Рис. 65

Проведем в данной плоскости горизонталь h(рис. 66). Прямаяn, перпендикулярная к прямойh, перпендикулярна и к следу плоскости_H(KLH) (рис. ).

Угол наклона прямой nк плоскости H определяется как угол между прямой и ее проекцией на плоскость H. СтроимКК'H (рис. 66). Тогда угол— искомый угол наклона прямойnк плоскости H.

На рис. построена линия наибольшего наклона плоскости к горизонтальной плоскости проекций — прямаяn. Угол наклона плоскостик плоскости H получают при определении натуральной величины отрезкаКМпри построении прямоугольного треугольника по проекциям K'M' иK”.

Рис. 66