1. Бірінші ретті дифференциалдық теңдеулер. Негізгі түсініктер

Дифференциалдық теңдеулер – ізделінетін функцияны оның әр түрлі ретті туындыларымен (немесе дифференциалдарымен) және тәуелсіз айнымалылармен байланыстыратын теңдеулер. Егер белгісіз функция тек бір ғана тəуелсіз айнымалыдан тəуелді болса, ондай теңдеуді жəй дифференциалдық теңдеу деп, ал бірнеше аргументтен тəуелді болса, ондай теңдеуді дербес туындылы дифференциалдық теңдеу деп атайды. Теңдеуге кіретін туындылардың ең жоғарғы реті дифференциалдық теңдеудің реті деп саналады. Бірінші ретті сызықты теңдеулер . Белгісіз функция мен оның туындысы сызықты түрде , яғни бірінші дəрежеде байланысқан теңдеуді сызықты дифференциалдық теңдеу деп атайды . Сызықты теңдеудің келтірілген түрін қарастырайық: y ′+ p( x )y = q( x ) (1) Мұнда p(x), q(x) функциялары кейбір <a,b> аралығында анықталған жəне үздіксіз деп есептелінеді . Егер q(x) ≠ 0 болса , онда (1) теңдеуді біртексіз сызықты теңдеу деп , ал q(x)=0 болса , онда біртекті сызықты теңдеу деп атайды : y ′+ p( x )y = 0 (2) Көбінесе (2) теңдеуді (1) теңдеудің сəйкес біртектісі деп атайды . Біртекті (2) теңдеу айнымалылары ажыратылатын теңдеу . Екі жағын у-ке бөліп , мынандай теңдеу аламыз :

Осы қатынасты интегралдасақ:

ln| y| + ∫ p( x)dx=lnC

өрнегін аламыз . Логарифмсіз жазсақ,

(3) түріндегі (2) теңдеудің жалпы шешімін аламыз. Егер y=0 жағдайды қарастырсақ, ол осы жалпы шешімнің С=0 болғандағы мəніне сəйкес келетін шешім . Сондықтан y=0 – дербес шешім . Оны нөлдік немесе триви aл шешім деп те атайды жəне ол барлық уақытта бар шешім . Біртекті (2) теңдеудің (3) жалпы шешімін Коши түрінде жазсақ, былай жазылады : y= (4) мұнда х0 -тұрақты сан , ал у0 – кез келген сан деп есептелінеді . Біртекті теңдеу шешімдерінің екі қасиетін атап өтейік : 1. Егер у1 жəне у2 функциялары (2) теңдеудің шешімдері болса , онда олардың қосындысы : у = у1+у2 функциясы да сол теңдеудің шешімі болады . 2. Егер у1 функциясы (2) теңдеудің шешімі болса , онда y = Cy1 функциясы да ( С – кез келген сан ) сол теңдеудің шешімі болады .

2. Дифференциалдық теңдеулердің геометриялық мән – мағынасы. Векторлар өрісі. Изоклина.

3. Бірінші ретті теңдеулер үшін Коши есебі.  (1) Практикалық есептерді шешкенде теңдеудің барлық шешімдерін табу емес, белгілі бір шарттарды қанағаттандыратын шешімді табу талап етіледі. Осындай есептің бір түрі Коши есебі деп аталады. Ол былай қойылады: берілген (1) теңдеудің барлық шешімдерінің арасынан тәуелсіз айнымалының берілген мәнінде берілген у₀ мәнін қабылдайтын, яғни

(12)

шартын қанағаттандыратын шешімін табу керек. Қысқаша бұл есепті былай жазады:

(13)

Мұндағы, сандарын бастапқы мәндер, ал (12) теңдікті бастапқы шарт деп атайды.Сонымен , бірінші ретті теңдеудің қалыпты түрін алайық: 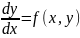(1) мұндағы, f ( x,y ) функциясы жазықтықтағы кейбір D ⊂ тұйық облысында анықталсын . Осы теңдеу үшін бастапқы y(x0)=y0 (2) шартын қанағаттандыратын шешімді табу есебі қойылсын . Бұл жерде ( x0 ,y 0) нүктесі сол D облысының ішінде жатады деп есептелінеді , ал D облысын , əдетте , төртбұрыш түрінде алады : { (x,y)|x-x0| |y-y0| (3) мұндағы, a жəне b- белгілі оң сандар . Теорема -1. Егер f ( x,y ) функциясы D облысында төмендегідей екі шартты қанағаттандырса : 1) екі аргументі бойынша үздіксіз , сондықтан ол шектелген : sup|f ( x,y )|= M M>0 2) y аргументі бойынша Липшиц шартын қанағаттандырады , яғни кез келген екі нүкте үшін |f(x,y1)- f(x,y2)| (4) теңсіздігі орындалады , L>0, онда бастапқы (2) шартты қанағаттандыратын , |x-x0| ), аралығында анықталған үздіксіз дифференциалданатын жалғыз ғана y= шешім бар болады . Дəлелдеуі . 1 . Алдымен Коши есебінің интегралдық теңдеуге пара -пар екендігін көрсетейік . Айталық, функциясы y= (2) шартты қанағаттандыратын , |x-x0|≤ h кесіндісінде анықталған (1) теңдеудің шешімі болсын Соңғы тепе -теңдікті х0-ден х-қа дейін интегралдасақ, мынандай тепе -теңдік аламыз : Бұдан y= функциясының (5) интегралдық теңдеудің шешімі болатынын көреміз Бұдан шығатын қорытынды – Коши есебінің шешімін табу үшін интегралдық теңдеудің шешімінің барлығын жəне жалғыздығын дəлелдесек жеткілікті . 2. Интегралдық теңдеудің шешімін біртіндеп жуықтау əдісімен іздейміз . Бұл əдісті Пикар əдісі деп те атайды . Бастапқы нөлдік жуықтау ретінде ізделініп отырған функцияның алғашқы y0 мəнін аламыз да , бірінші жуықтау үшін (6) өрнегін жазамыз , ал екінші жуықтау үшін (7) өрнегін жазамыз . Жалпы , кез келген n-ші жуықтауды мына түрде жазамыз : (8) Коши есебінің шешімінің жалғыздығын дəлелдеу үшін алдымен Гронуолл леммасын келтірейік . Лемма . Кейбір a,b аралығында үздіксіз u(t ) ≥0 f(t) ≥0 функциялары жəне C>0 тұрақты саны үшін теңсіздігі орындалса , онда одан мынандай теңсіздік алуға болады :

4. Коши есебінің геометриялық мән - мағынасы. (1) Практикалық есептерді шешкенде теңдеудің барлық шешімдерін табу емес, белгілі бір шарттарды қанағаттандыратын шешімді табу талап етіледі. Осындай есептің бір түрі Коши есебі деп аталады. Ол былай қойылады: берілген (1) теңдеудің барлық шешімдерінің арасынан тәуелсіз айнымалының берілген мәнінде берілген у₀ мәнін қабылдайтын, яғни

(12)

шартын қанағаттандыратын шешімін табу керек. Қысқаша бұл есепті былай жазады:

(13)

Мұндағы, сандарын бастапқы мәндер, ал (12) теңдікті бастапқы шарт деп атайды. Осыған байланысты Коши есебін бастапқы есеп дейді. Коши есебіне геометриялық түсініктеме беруге болады: (1) теңдеудің барлық интегралдық қисықтарының ішінен белгілі бір нүктесі арқылы өтетінін табу керек.