Раздел 4. Уравнения и неравенства. Тема 4.1. Уравнения и системы уравнений. Уравнения и системы уравнений.
Линейные уравнения.
Уравнение вида
,
где
— переменная, а
и
— действительные числа, причем
,
называется
линейным
уравнением.
Числа
и
называются
коэффициентами
уравнения. Решение линейных уравнений
основано на двух сформулированных выше
теоремах.
Пример 1.
Решить уравнение
.
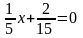Данное уравнение
— линейное; здесь
,
.
Решение проведем двумя способами.
I
способ.
Согласно теореме 1, уравнение
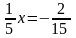равносильно данному.
Разделим обе части этого уравнения на
коэффициент при
,
что по теореме 2 приводит к равносильному
уравнению; тогда получим
— корень уравнения.
II
способ.
Умножим обе части заданного уравнения
на 15 (такое преобразование называется
освобождением от знаменателей):
.
В силу теоремы 2, полученное уравнение
равносильно данному. Далее, имеем:
,
.
Пример 2.
Решить уравнение
.
Освободимся от знаменателей, для чего умножим обе части уравнения на 21:
.
Далее, имеем:
;
;
;
.
Пример 3.
Решить уравнение
.
Последовательно получаем:
;
.
Перенесем все члены уравнения из правой части уравнения в левую, изменив при этом знаки:
.
После приведения подобный членов получаем
,
,
.
Уравнения с переменной в знаменателе.
Рассмотрим
уравнения вида
,
где
—
переменная;
и
—
действительные числа;
— многочлен, а также уравнения, сводимые
к указанному виду. Эти уравнения не
являются линейными, но в процессе решения
они сводятся к линейным.
Решение
уравнения
основано на следующем утверждении:
дробь
равна
нулю тогда и только тогда, когда ее
числитель равен нулю, а знаменатель
отличен, от нуля (на нуль делить нельзя!).
Это записывают так:
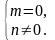
Таким
образом, чтобы решить уравнение
,
нужно сначала найти корень линейного
уравнения
,
а затем выяснить, является ли при
найденном значении переменной
истинным высказывание
.
Если
это высказывание истинно, то найденный
корень линейного уравнения
является и корнем уравнения
;
если же это высказывание ложно (истинно
высказывание
),
то уравнение
не имеет, корней.
Пример
1.
Решить уравнение
.
Воспользовавшись указанным выше условием равенства дроби нулю, получим систему
Из
уравнения
находим
.
Так как высказывание
истинно, то
— корень заданного уравнения.
Пример
2. Решить уравнение
.
Имеем
.
Из
уравнения
находим
.
Высказывание
ложно; значит, данное уравнение не имеет
корней.
Пример
3. Решить уравнение
.
Имеем
,
,
,
.
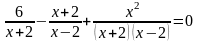Из
уравнения
находим
.
Высказывание
истинно; значит,
— корень данного уравнения.
Основные приемы их решения.
Уравнение
вида
,
где
a,
b, c -
действительные числа, причем a≠0,
называют квадратным
уравнением.
Числа a, b, c носят следующие названия a - первый коэффициент, b - второй коэффициент, c - свободный член.
Выражение D = b2- 4ac называют дискриминантом квадратного уравнения.
Система
вида
,
называется системой нелинейных уравнений
с двумя переменными, если хотя бы одно
из уравнений нелинейное.
Решением
системы нелинейных уравнений
является пара чисел (a,
b)
, при подстановке которой в исходную
систему получаются верные тождества:
.
Нелинейные системы не имеют универсального способа решения, поэтому при решении конкретной системы уравнений нужно учитывать особенности заданных уравнений, переходя к равносильным системам.
Основные методы решения систем нелинейных уравнений:
метод подстановки;
метод введения новых переменных;
графический метод;
метод алгебраического сложения;
метод почленного умножения и деления;
метод математического подбора.
Системы нелинейных уравнений: примеры и достаточные знания, необходимые для решения заданий.
Метод подстановки.
Метод подстановки: одно из уравнений системы преобразуют к виду, разрешенному относительно одной переменной, например у выражают через х. Далее, полученное выражение подставляют вместо у во второе уравнение. В результате получается уравнение с одной переменной х. Находят корни этого уравнения, а затем, воспользовавшись выражением у через х, находят соответствующие значения у.
Пример 1. Решить систему уравнений
Из
первого уравнения находим
.
Подставим выражение
вместо
х
во второе уравнение
системы;
тогда
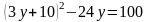
и, далее,
,
,
,
.
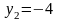Соответствующие значения х найдем из уравнения . Если у = 0, то х = 10; если у = - 4, то х = - 2. Итак, система имеет два решения: (- 2; - 4); (10; 0).
Пример 2. Решить систему уравнений
Из
второго уравнения системы находим
.
Подставив
выражение
вместо
у
в первое уравнение системы, имеем
,
28 = 1.
Полученное высказывание является ложным при любом х. Это значит, что заданная система уравнений не имеет решений.
Метод сложения.
Суть этого метода поясним на примерах.
Пример 1. Решить систему уравнений
(*)
Умножив обе части второго уравнения системы на 3, получим систему
(**)
равносильную данной на основании теоремы 1.
Сложим теперь оба уравнения полученной системы. Согласно теореме 2, система
(***)
равносильна системе (**). Система (***) преобразуется к виду
Из
уравнения
находим х=5. Подставив это значение в
уравнение 2х+3у=7, получим у
= -1.
Итак, (5; - 1) —решение системы (***), а значит, и решение равносильной ей системы (*).