Примеры выполнения заданий.

Пример 1. Вычислить: .

Решение:

Ответ: 8.

Пример 2. Вычислить: .

Решение:

Ответ: 15.

Пример 3. Вычислить:

Решение:

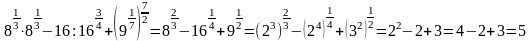
Ответ: 5.

Пример 4. Упростить: .

Решение:

Ответ: а^-2в¹³.

Пример 5.

Решение иррациональных уравнений.

Уравнения, в которых под знаком корня содержится переменная, называют иррациональными.

Методы решения иррациональных уравнений основаны на возможности замены иррационального уравнения рациональным уравнением, которое является его следствием. Чаще всего обе части уравнения возводят в одну и ту же степень. При этом получается уравнение, являющееся следствием исходного.

При решении иррациональных уравнений необходимо учитывать следующее:

1) если показатель корня - четное число, то подкоренное выражение должно быть неотрицательно; при этом значение корня также является неотрицательным.

2) если показатель корня - нечетное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак корня совпадает со знаком подкоренного выражения.

При возведении в квадрат обеих частей уравнения могут появиться лишние корни. Чтобы определить истинность найденных корней, каждый корень последнего уравнения подставляют в исходное уравнение. Значение переменной, которые при подстановке не дают истинных равенств, отбрасывают как посторонние корни.

Пример.		Решить уравнение  = 1 - х
Решение:
= 1 – х возведем в квадрат обе части уравнения. ( )  = (1 – х) ; 1+ 3х = x2 – 2x + 1; x2– 5x = 0. Решив это уравнение, находим корни . Проверка: если x = 0, то , 1 = 1 – верно; если х = 5, то , 4 = 4 – неверно.
Ответ:	х = 0

Решение показательных уравнений.

Показательным называют уравнение, содержащее переменную в показателе степени. Например, ; ; .

Показательные уравнения приводят к виду (где левая и правая части уравнения есть степени с одинаковым основанием).

Так как показательная функция при а монотонно возрастает на всей области определения (при 0 < а < 1 монотонно убывает), то каждое свое значение она принимает только один раз при одном значении аргумента, т. е. из равенства следует равенство v = u.

К уравнениям рассмотренного выше типа приводятся уравнения вида (где а и а ) путем представления единицы в виде степени числа с нулевым показателем: .

1. Простейшие уравнения, т.е. такие, левую и правую части которых можно привести к одному основанию решаются так:

2. Уравнения вида решаются вынесением за скобки степени с наименьшим показателем.

3. Уравнения, вида , решаются с помощью подстановки а^х = у и сводится к квадратному уравнению.

4. При решения уравнения вида обе части уравнения необходимо разделить на , т.к. ≠ 0 .

Пример.		Решить уравнение 5(4–x)/2 = 5–3
Решение:
приравняем показатели (4 – х)/2 = –3, 4 – х = –6, –х = –10, х = 10
Ответ:	х = 10
Пример.		Решить уравнение: 52x + 1 – 26 • 5x + 5 = 0
Решение:
Пусть 5x = y, причем у > 0. 5y2 – 26y + 5 = 0, D = 169 – 25 = 144, y1 = 5, y2 = 1/5. Найдем х, возвратившись к подстановке 5x = y 5x = 5 или 5x = 1/5 x = 1 x = – 1
Ответ:	x = 1 и x = –1

Тема 1.3. Логарифм.

Логарифм числа.

Логарифмом числа по основанию называется показатель степени, в которую надо возвести основание , чтобы получить число .

Из определения следует, что нахождение равносильно решению уравнения . Например, потому что

Виды логарифмов.

Наиболее широкое применение нашли следующие виды логарифмов.

• Натуральные логарифмы: , основание: число Эйлера (е)

• Десятичные логарифмы: , основание: число 10

Действия с логарифмами.

Основное логарифмическое тождество

Из равенства двух логарифмов следует равенство логарифмируемых выражений. В самом деле, если , то , откуда, согласно основному тождеству:

Логарифмы единицы и числа, равного основанию логарифма

Логарифм произведения, частного от деления, степени и корня:

Произведение
Частное от деления
Степень
Корень