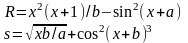3 Применение математического моделирования в экономике
С математическим моделированием мы знакомимся еще в школе. Сталкиваемся с ним и в университете, и на работе, и дома. Большинство математических моделей мы рассчитываем при помощи электронно-вычислительной техники, так как в большинстве своем задачи очень громоздкие и требует точности. Такие задачи мы решаем с помощью Microsoft EXCEL. Рассмотрим пример.
1.Постановка задачи
Вычислить на ЭВМ значения переменных представленные в Таблица 1 по заданным расчетным формулам и наборам исходных данных. И сравнить полученные значения со значениями, полученными в EXCEL. На печать вывести значения вводимых исходных данных и результаты вычислений, сопровождая вывод наименованиями выводимых переменных.
Таблица 3.1 – Исходные данные[20]
Расчетные формулы |
Значения исходных данных |
1 |
2 |
|
a=0,7 b=0,05 x=0,5 |
В пункте 2. 4 этапы построения экономико - математической модели представлена общая схема процесса создания математической модели. В соответствии с этой схемой составляем алгоритм действий для выполнения предложенного задания.
Рисунок 3.1 – Алгоритм выполнения действий[18]
Каждый блок должен идти в определенной строгой последовательности.
Пошаговые действия:
1 - ввод исходных данных a, b, x.
2 - вывод исходных данных a, b, x.
3 - ввод формулы для неизвестной R.
4 - ввод формулы для неизвестной s.
5 - вывод неизвестных.
Только после составления алгоритм можно приступать к написанию программы. Создаем лист EXCEL, в нем открываем вкладку разработчик -VisualBasic. Выполняем команды Сервис- Макрос-Редактор VisualBasic. Затем Вставка-Модуль, Вставка-Процедура. А затем набираем текст программы[19].
Рисунок 3.2 – Текст программы
Для проверки работы программы вводим известные значения.
Рисунок 3.3 – Значение х
Рисунок 3.4 – Значение а
Рисунок 3.5 – Значение b
Рисунок 3.6 – Контроль ввода исходных данных
Рисунок 3.7 – Результаты вычислений
Этот пример наглядно показывает какую большую роль математическое моделирование играет как в экономике, так и в жизни.
Рассмотрим более глобальный пример участия математического моделирования в экономике.
С помощью математического моделирования можно рассчитать уровень инфляции в стране.
Уровень инфляции в Российской Федерации в 2016 году[17]:
В октябре 2016 года уровень инфляции в России составил 0,43%, что на 0,26 больше, чем в сентябре 2016 года и на 0,31 меньше, чем в октябре 2015 года. Вместе с этим, инфляция с начала 2016 года составила 4,50%, а в годовом исчислении - 6,09%.
В 2016 Россия занимает 13 место по уровню инфляции в мире.
Инфляция в России, как и во многих странах, рассчитывается на основе Индекса Потребительских Цен на Товары и Услуги. Примечательно, что в России этот индекс рассчитывается только с 1991 года, т.к. во времена СССР и плановой экономики официально уровень инфляции не рассчитывался.
При этом под Потребительскими Ценами подразумевается конечная цена, которую платит покупатель товара или услуги и которая включает в себя налоги и сборы.
Таблица 3.2 – инфляция в России [16]
|
Янв |
Фев |
Мар |
Апр |
Май |
Июн |
Июл |
Авг |
Сен |
Окт |
Ноя |
Дек |
За год |
2016 |
0.96 |
0.63 |
0.46 |
0.44 |
0.41 |
0.36 |
0.54 |
0.01 |
0.17 |
|
|
|
4.05 |
2015 |
3.85 |
2.22 |
1.21 |
0.46 |
0.35 |
0.19 |
0.80 |
0.35 |
0.57 |
0.74 |
0.75 |
0.77 |
12.91 |
2014 |
0.59 |
0.70 |
1.02 |
0.90 |
0.90 |
0.62 |
0.49 |
0.24 |
0.65 |
0.82 |
1.28 |
2.62 |
11.36 |
2013 |
0.97 |
0.56 |
0.34 |
0.51 |
0.66 |
0.42 |
0.82 |
0.14 |
0.21 |
0.57 |
0.56 |
0.51 |
6.45 |
2012 |
0.50 |
0.37 |
0.58 |
0.31 |
0.52 |
0.89 |
1.23 |
0.10 |
0.55 |
0.46 |
0.34 |
0.54 |
6.58 |
2011 |
2.37 |
0.78 |
0.62 |
0.43 |
0.48 |
0.23 |
-0.01 |
-0.24 |
-0.04 |
0.48 |
0.42 |
0.44 |
6.10 |
2010 |
1.64 |
0.86 |
0.63 |
0.29 |
0.50 |
0.39 |
0.36 |
0.55 |
0.84 |
0.50 |
0.81 |
1.08 |
8.78 |
2009 |
2.37 |
1.65 |
1.31 |
0.69 |
0.57 |
0.60 |
0.63 |
0.00 |
-0.03 |
0.00 |
0.29 |
0.41 |
8.80 |
2008 |
2.31 |
1.20 |
1.20 |
1.42 |
1.35 |
0.97 |
0.51 |
0.36 |
0.80 |
0.91 |
0.83 |
0.69 |
13.28 |
2007 |
1.68 |
1.11 |
0.59 |
0.57 |
0.63 |
0.95 |
0.87 |
0.09 |
0.79 |
1.64 |
1.23 |
1.13 |
11.87 |
2006 |
2.43 |
1.66 |
0.82 |
0.35 |
0.48 |
0.28 |
0.67 |
0.19 |
0.09 |
0.28 |
0.63 |
0.79 |
9.00 |
2005 |
2.62 |
1.23 |
1.34 |
1.12 |
0.80 |
0.64 |
0.46 |
-0.14 |
0.25 |
0.55 |
0.74 |
0.82 |
10.91 |
2004 |
1.75 |
0.99 |
0.75 |
0.99 |
0.74 |
0.78 |
0.92 |
0.42 |
0.43 |
1.14 |
1.11 |
1.14 |
11.74 |
2003 |
2.40 |
1.63 |
1.05 |
1.02 |
0.80 |
0.80 |
0.71 |
-0.41 |
0.34 |
1.00 |
0.96 |
1.10 |
11.99 |
2002 |
3.09 |
1.16 |
1.08 |
1.16 |
1.69 |
0.53 |
0.72 |
0.09 |
0.40 |
1.07 |
1.61 |
1.54 |
15.06 |
2001 |
2.76 |
2.28 |
1.86 |
1.79 |
1.78 |
1.62 |
0.45 |
0.01 |
0.60 |
1.09 |
1.36 |
1.60 |
18.58 |
2000 |
2.33 |
1.04 |
0.64 |
0.89 |
1.75 |
2.55 |
1.79 |
0.98 |
1.32 |
2.11 |
1.52 |
1.64 |
20.20 |
1999 |
8.38 |
4.13 |
2.79 |
3.03 |
2.22 |
1.91 |
2.82 |
1.16 |
1.48 |
1.37 |
1.23 |
1.26 |
36.56 |
1998 |
1.51 |
0.89 |
0.64 |
0.38 |
0.50 |
0.08 |
0.17 |
3.67 |
38.43 |
4.54 |
5.67 |
11.61 |
84.44 |
1997 |
2.34 |
1.54 |
1.43 |
0.96 |
0.94 |
1.10 |
0.93 |
-0.14 |
-0.30 |
0.17 |
0.61 |
0.96 |
11.03 |
1996 |
4.11 |
2.79 |
2.80 |
2.16 |
1.60 |
1.17 |
0.72 |
-0.21 |
0.33 |
1.20 |
1.88 |
1.42 |
21.81 |
1995 |
17.77 |
11.02 |
8.94 |
8.47 |
7.93 |
6.66 |
5.38 |
4.56 |
4.46 |
4.72 |
4.56 |
3.20 |
131.33 |
Текущий уровень инфляции
Уровень инфляции в октябре 2016: 0,43%
Уровень инфляции с начала 2016 года: 4,50%
Уровень инфляции в сентябре 2016: 0,17%
Уровень инфляции в октябре 2015: 0,74%
Уровень инфляции в октябре 2015 с начала года: 11,21%
Уровень инфляции в 2015: 12,91%
Уровень инфляции за 12 месяцев: (годовое исчисление)6,09%
Уровень инфляции за 60 месяцев (5 лет): 50,35%
Уровень инфляции за 120 месяцев (10 лет): 140,58%
Накопленная инфляция за весь период (1995-2016): 4 517.35%.
Среднегодовая инфляция в России за последние 10 лет: 9.20%
Математическое моделирование используется как на микроуровне, так и на макроуровне.
Рисунки 3.1-3.7 четко показывают использование математического моделирования на микроуровне (таким задачам нас учат уже на первом курсе университета). Из чего можно сделать вывод, что математическое моделирование является неотъемлемой частью человеческой жизни.
Таблица 3.1 иллюстрирует использование моделирования на макроуровне (на примере Российской Федерации). Таблица четко дает понять динамику инфляции за 20-ти летний интервал. Проанализировав таблицу можно заметить что инфляционные изменения идут на спад. А это в свою очередь значит что государство укрепляет свои позиции, а следом за государством укрепляет свои позиции и государственная валюта – рублю.