Билет 12

Сложные суждения и их виды. Логическая форма сложных суждений. Правила по отношению к демонстрации.

Сложным суждением называется суждение, содержащее в себе другие суждения в качестве логической части.

Сложные суждения и действия с ними лежат в основе одной из первых и наиболее простых теорий современной логики – логики высказываний. В языке логики высказываний не выявляется состав простых суждений, их субъектно-предикатная структура, а анализируются лишь логические формы сложных высказываний (суждений).

Язык логики высказываний содержит следующие символы: 1) Знаки для простых суждений: p, q, r, s, p1 , q1 , r1 , s1 , p2 … 2) Знаки для логических союзов: & (конъюнкция),  (дизъюнк- ция),  (строгая дизъюнкция), → (импликация), ≡ (эквивалентность), ¬ (отрицание). 3) Технические знаки: ( , ) – левая и правая скобки. С использованием этих знаков строится все множество сложных суждений. Кроме того, мы можем использовать заглавные латинские буквы A, B, C, D и другие для обозначения произвольных (в том числе и слож- ных) выражений нашего языка. Таким образом, мы получаем следующий язык: 1. p, q, r, s, p1 ,q1 , … – простые суждения.

2. Если А и В – суждения, то (А & В), (А  В), (А  В), (А → В), (А ≡ В), (¬А). 3. Ничто иное не является суждением. Выявить логическую форму сложного суждения – это значит записать его в виде правильно построенного выражения на языке логики высказываний. Например, высказывание – «Если звезды зажигают – значит – это кому-нибудь нужно?» – будет представлено в виде импликации (p → q); а логической формой поэтических строк – «Прозрачный лес один чернеет, и ель сквозь иней зеленеет, и речка подо льдом блестит» – будет конъюнкция ( p & q & r).

Виды сложных суждений и семантические таблицы истинности Вид сложного суждения определяется логическим союзом, с помощью которого оно образовано. Истинность или ложность сложного суждения зависят, во-первых, от истинности или ложности простых суждений, входящих в его состав, во-вторых, от свойств соответствующих логических союзов. Определяется эта зависимость посредством специальных семантических таблиц. Рассмотрим возможные виды сложных суждений и условия их истинности.

1. Соединительное суждение – конъюнкция. В русском языке ему соответствует союз «и». Логическая форма: (А & В). При каких условиях высказывание «Я пойду завтра на лекцию и зайду в библи- отеку» будет истинным? Конечно, если будут выполнены обе его составляющие. Если же Вы не сделаете хотя бы одного (не зайдете в библиотеку), оно будет ложным. Оформим это в виде таблицы (табл. 5).

Принцип построения таблицы: в двух левых столбцах мы выписываем простые суждения, входящие в состав сложного, т. е. А и В, и перечисляем все возможные сочетания их истинностных значений (они могут быть оба истинными, или одно истинно, а другое ложно, или оба ложны). Буквой «И» обозначаем истину, буквой «Л» – ложь. В правой половине таблицы мы выписываем само сложное суждение, а под ним, в четырех строках, все возможные для него истинностные значения. Как видим, конъюнкция будет истинной только в первой строке, т. е. тогда, когда будут истинны оба составляющие ее высказывания.

2. Р азделительное суждение – дизъюнкция. Ему соответствует союз «или». Логическая форма: (А  B). Дизъюнкция означает, что по крайней мере одно из двух суждений: А или В, или оба вместе должны быть истинными. Дизъюнкции соответствует таблица 6. Таким образом, дизъюнкция будет ложной только в одной строке таблицы – когда ложны оба составляющих ее высказывания.

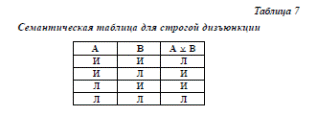
3. Строго-разделительное суждение – строгая дизъюнкция. В естественном языке ей соответствует союз «либо…, либо…», что предполагает выбор одной из альтернатив, но не обеих вместе. Альтернативами в данном случае называются несовместимые суждения А и В. Логическая форма: (А  В). Строгая дизъюнкция отличается от обычной только первой строкой (табл. 7).

4. Условное суждение – импликация. В естественном языке импликации соответствует союз «если…, то…». Логическая форма: (А → В). Первый аргумент импликации (А) называется антецедентом, или условием, второй (В) – консеквентом, или следствием. Импликация будет ложной только в одном случае: когда условие выполнено (А истинно), а следствие не наступило (В ложно). Возьмем высказывание: «Если я устал, то не могу работать». Человек устал, но может работать. Значит, его первоначальное высказывание было ложным (табл. 8).

5. С уждение эквивалентности. В языке эквивалентности соот- ветствует союз «…тогда и только тогда, когда…». Логическая форма: (А ≡ В). Данное суждение истинно тогда и только тогда, когда его аргументы (А и В) либо истинны, либо ложны (табл. 9).

6. Отрицательные суждения – отрицание. В языке им соответствуют выражения «не», «неверно, что…». Отрицание действует только на одно суждение, поэтому таблицу можно представить так (табл. 10).

Отметим, что смысл определенных нами с помощью таблиц логических союзов (конъюнкции, дизъюнкции и т. д.) лишь приблизительно совпадает со смыслом грамматических союзов (и, или и т. д.), которые в повседневном обиходе употребляются, как правило, неоднозначно.

Правила по отношению к демонстрации.

Правилами по отношению к демонстрации являются правила используемого в доказательстве умозаключения, поскольку формально-логические доказательства всегда протекают в форме какого- либо умозаключения. Иначе говоря, используемые в демонстрации умозаключения должны быть правильными, и должны быть соблюдены условия их применимости. Нарушение хотя бы одного правила умозаключения приводит к несостоятельности всего доказательства, что выражается в ошибке «мнимое следование» (или «не следует» – non sekietur). Это значит, что между тезисом и аргументами отсутствует логическая связь. В качестве примера ошибки «не следует» приведем силлогизм из книги Л. Кэрролла «История с узелками»: Никому из тех, кто хочет ехать поездом, кто не может достать экипаж и у кого нет времени, чтобы спокойно дойти до станции, не миновать пробежки. Эти туристы намереваются ехать поездом, но не могут достать экипаж, зато у них достаточно времени, чтобы спокойно дойти до станции. Этим туристам не придется бежать. «Вот еще один удобный случай, любезный читатель, – пишет Л. Кэрролл, – чтобы разыграть твоего невинного друга. Предложите ему силлогизм, сформулированный в условии задачи, и спросите, что он думает о заключении. Скорее всего он ответит: – Оно абсолютно правильно! А если твоя драгоценная книга утверждает, будто оно неправильно, не верь ей! Ведь не думаешь же ты, что этим туристам придется бежать, чтобы успеть на поезд? Если бы я был одним из них и знал, что посылки истинны, то мне было бы совершенно ясно, что бежать не придется, и я бы преспокойно отправился на станцию пешком! На это вы должны возразить: – А если за тобой погонится бешеный бык?.. И тут настанет удобный момент для того, чтобы разъяснить ему удобный способ проверки правильности силлогизма: если можно придумать обстоятельства, которые, не влияя на истинность посылок, сделают заключение ложным, то силлогизм неправилен».