3. Кореляція

Можна без перебільшень сказати, що у всіх педагогічних дослідженнях головний інтерес становить вивчення педагогічних явищ у взаємозв'язку одне з одним, тобто причинної залежності між ними. Зв'язки (залежності) між двома чи більше змінними у статистиці називають кореляцією. При вивченні кореляцій намагаються встановити, чи існує, якийсь зв'язок між двома показниками в одній вибірці (наприклад, між вмінням виділяти головне в навчальному матеріалі і вмінням систематизувати вивчене), або між двома річними вибірками (наприклад, при порівнянні пар учнів з експериментальної і контрольної груп), і якщо цей зв'язок існує, то чи супроводжується збільшення одного показника зростанням (позитивна кореляція) або зменшенням (від'ємна кореляція) іншого.

Оцінюється кореляція за допомогою значення коефіцієнта кореляції, який є мірою ступеня і величини цього зв'язку.

Коефіцієнт кореляції r змінюється від +1 до -1. Ступінь відмінності коефіцієнта кореляції від нуля (в межах від +1 до -1) виражає силу (міцність) зв'язку між ознаками. Про міцну кореляцію можна говорити тільки в тих випадках, коли коефіцієнт кореляції є більшим від 0,7. Коефіцієнт кореляції близько 0,5 - 0,7 прийнято вважати середнім, а коефіцієнт менший від 0,5 - слабким. Якщо r дорівнює 1 (або -1), то ми маємо пряму (або обернену) функціональну залежність. Якщо r дорівнює 0, то зв'язок між ознаками відсутній. При позитивній кореляції залежність між ознаками пряма: зі збільшенням однієї ознаки збільшується й інша. При негативній кореляції залежність між ознаками обернена: збільшення однієї ознаки відповідно пов'язане зі зменшенням іншої ознаки.

Коефіцієнт кореляції обчислюють за формулою:

,

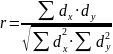де d_x, - відхилення від середньої М_х, a d_v - відхилення від середньої М_у. Індекси х і у означають ознаки (показники X і Y). Для оцінки вірогідності кореляції (визначення рівня значущості) можна скористатися критерієм Стьюдента t:

Вірогідність кореляційного зв'язку безпосередньо пов'язана з кількістю проведених досліджень, тобто з обсягом сукупності п. Сильні кореляційні зв'язки можна з високою вірогідністю довести навіть при малому обсязі експериментального матеріалу. Зате слабкі взаємовпливи можна вірогідно виявити лише на основі великого обсягу досліджень.

Коефіцієнтів кореляції існує багато. Розглянемо лише частину з них, які враховують наявність лінійного зв'язку між змінними. Їх вибір залежить від шкал вимірювання змінних, залежність між якими необхідно оцінити. Найчастіше в педагогіці застосовуються коефіцієнти Браве-Пірсона і Спірмена.

Розглянемо обчислення значень коефіцієнтів кореляції на конкретних прикладах.

Приклад 1. Нехай дві змінні, що порівнюються, х (участь в роботі наукових товариств) і у (вступ до університету) вимірюється в дихотомічній шкалі (частковий випадок шкали найменувань). Для визначення зв'язку скористаємося коефіцієнтом Браве-Пірсона.

У тих випадках, коли немає потреби підраховувати частоту появи різних значень змінних х і у, зручно обчислювати коефіцієнт кореляції за допомогою таблиці спряження (таблиці 17- 19), яка показує кількість спільних появ пар значень п за двома змінними (ознаками). А - кількість випадків, коли змінна х дорівнює нулю, і одночасно змінна у має значення, яке дорівнює одиниці; В - кількість випадків, коли змінні х і у мають одночасно значення, які дорівнюють одиниці; С - кількість випадків, коли змінні х і у мають одночасно значення, які дорівнюють нулю; D - кількість випадків, коли змінна х має значення, яке дорівнює одиниці, і одночасно змінна y має значення, яке дорівнює нулю.

Таблиця 7