Задание 6

Пункт по ремонту квартир работает в режиме отказа и состоит из двух бригад. Интенсивность потока заявок, производительность пункта

Определить вероятность того, что оба канала свободны, один канал занят, оба канала заняты, вероятность отказа, относительную и абсолютную пропускные способности, среднее число занятых бригад.

Интенсивность потока заявок	Интенсивность потока обслуживания
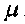
0,58	0,69

Решение:

Каждая система массового обслуживания включает в свою структуру некоторое количество обслуживающих устройств, называемых каналами обслуживания. Обслуживание заявок происходит за неизвестное, обычно случайное время и зависит от множества самых разнообразных факторов. Случайный характер потока заявок и времени их обслуживания приводит к неравномерности загрузки СМО- перегрузке с образованием очередей заявок или недогрузке с простаиванием её каналов. Каждая СМО в зависимости от своих параметров и правил организации её работы обладает определённой эффективностью функционирования (пропускной способностью), позволяющей ей более или менее успешно выполнять предназначенные ей функции. Для изучения процессов построения деятельности фирмы необходим анализ математической модели потока.

Предельные характеристики эффективности функционирования для многоканальной СМО с отказами приведены в таблице:

Характеристика в момент времени t	Формулы	Ответ
1. коэффициент использования		0,841
2.вероятность того, что оба канала свободны		0,457
3.вероятность занятости одного канала		0,384
4. вероятность занятости двух каналов		0,162
5. вероятность отказа в заявке		0,162
6. относительная пропускная способность СМО		0,838
7.абсолютная пропускная способность СМО		0,486
8.среднее время обслуживания заявок		1,449
9. среднее число занятых каналов		0,704

Решение:

Определим среднее время обслуживания заявки: = 1 : 0,69 = 1,449

Рассчитаем коэффициент использования = 0,58 : 0,69 = 0,841 – это количество заявок, поступающих за время использования одной заявки.

Вероятность того, что оба канала будут свободны:

1 : ( 1 + 0,841 + (0,841 * 0,841) = 1 = 0,457

2 2,19

= 0,841* 0,457 = 0,384

= 0,5 * (0,841 * 0,841) * 0,457 = 0,162

Отсюда = 0,162 , то есть из каждых 100 заявок 16 получат отказ,

= 1 – 0,162 = 0,838

= 0,58 * 0,838 = 0,486, это меньше производительности пункта.

= 0,486 : 0,69 = 0,704 . Среднее число занятых бригад - две.

Кроме рассмотренных, существуют также другие разновидности СМО, определить их предельные характеристики возможно также с помощью ЭВМ.

Заключение:

Все этапы экономико-математического моделирования , как постановка проблемы, построение математической модели, анализ математической модели, подготовка исходной информации, численное решение, анализ численных результатов и их применение находятся в тесной взаимосвязи. Могут иметь место возвратные связи этапов. Так, на этапе построения модели может выясниться, что постановка задачи или противоречива, или приводит к слишком сложной математической модели; в этом случае исходная постановка задачи должна быть скорректирована. Наиболее часто необходимость возврата к предшествующим этапам моделирования возникает на этапе подготовки исходной информации. Если необходимая информация отсутствует или затраты на её подготовку слишком велики, то приходится возвращаться к этапам постановки задачи и её формализации, чтобы приспособиться к доступной исследователю информации. Кроме того, начав исследование с построения простой модели, можно получить полезные результаты, а затем перейти к созданию более сложной и более совершенной модели, включающей в себя новые условия и более точные математические зависимости.

Список использованной литературы:

1. Математические модели в экономике. Учебно- методическое пособие М.Г. Сидоренко г. Томск 2000год.

2. Экономико- математические методы и прикладные модели: Учебное пособие для ВУЗов В.В.Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др. под редакцией В. В. Федосеева.- М. ЮНИТИ, 1999г.

3. Шелобаев С. И. Математические методы и модели в экономике, финансах, бизнесе: Учебное пособие для ВУЗов.- М.: ЮНИТИ-ДАНА, 2000г.

4. Малыхин В. И. Математическое моделирование экономики: Учебно-практическое пособие. _ М.: Издательство УРАО, 1998 г.

5. Исследование операций. 2. Модели и применения. Пер. с англ.Под ред. ДЖ.Моудера, С.Элмаграби.- М.: Мир, 1981 г.

Багаева Т. В.