3. Биномиальная модель Кокса–Росса–Рубинштейна.

Допустим сначала, что за каждый шаг по времени цена финансового актива может возрасти или понизиться только на определенную свою долю. Если в момент времени t цена равна S, то в момент t + D t она может либо возрасти до uS, либо понизиться до dS. Допустим, что имеется колл-опцион на этот актив, имеющий в момент t цену С. При росте цены основного актива до uS цена опциона также возрастет до некоторой величины Сuр, а при понижении цены до dS— понизится до величины Cdown Эти параллельные изменения цен показаны на рисунке. Так как возможны ровно два варианта изменения цены основного актива, то этот процесс естественно назвать биномиальным.

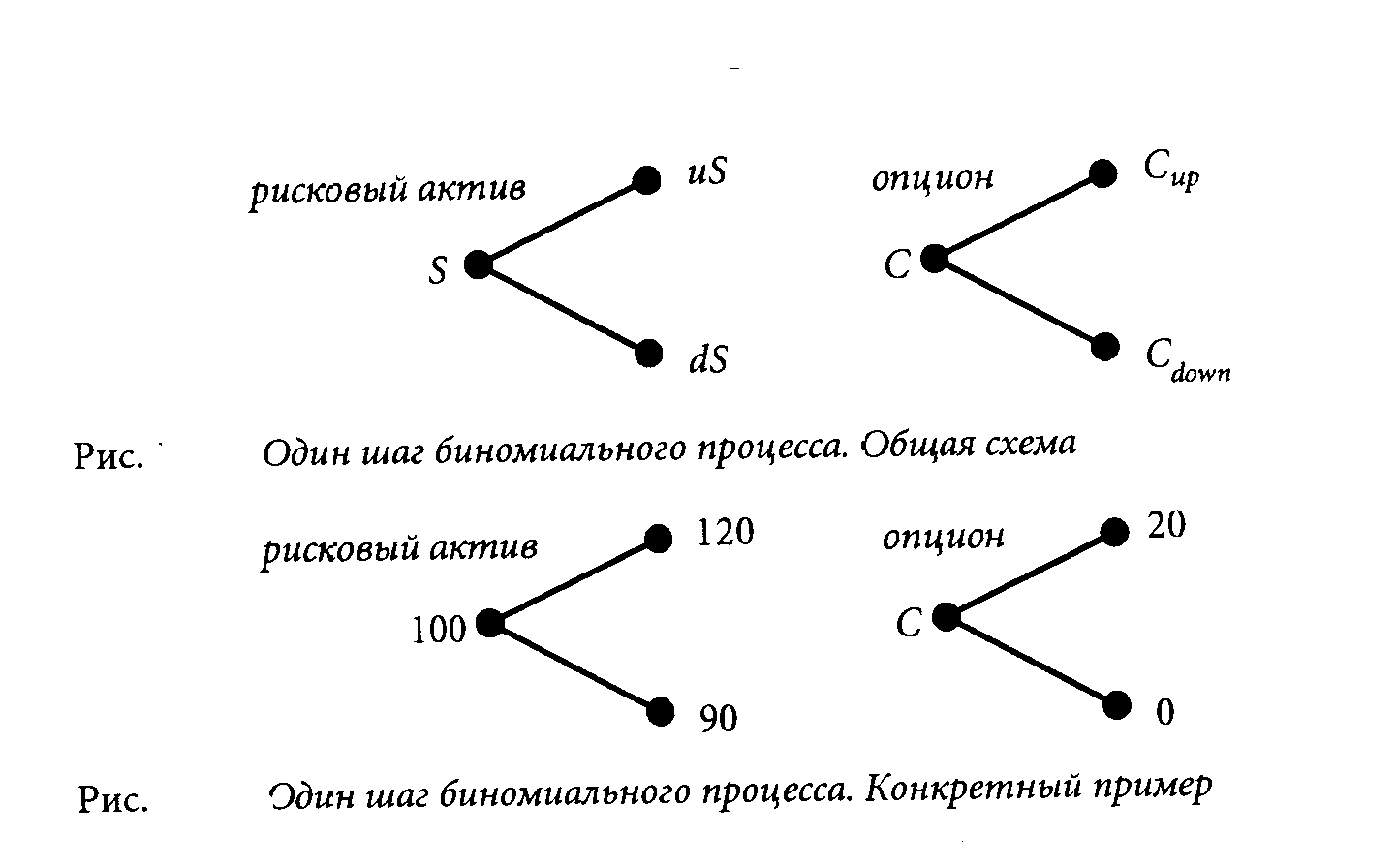
Например, пусть S = 100, и = 1.20, d = 0.90, опцион имеет цену исполнения 100 и его погашение произойдет через один шаг по времени. Тогда при росте цены активов до 120 опцион при исполнении будет стоить 20, а если цена упадет до 90, то опцион при исполнении обесценится. Этот конкретный сценарий показан на упомянутом рисунке.

Единственная неизвестная величина на — это С, стоимость колл-опциона за один шаг до исполнения. Мы покажем, что эту величину можно найти с помощью построения безрискового хеджа из опциона и основных активов.

Рассмотрим портфель, полученный в результате:

a) продажи трех колл-опционов по цене С каждый,

b) покупки двух единиц основных активов по цене 100 каждая,

c) взятия 163.64 в заем на один рассматриваемый период времени под 10%.

 

Чистый поток наличности при формировании портфеля составит: 3 С-200 + 163.64 = ЗС-36.36. При исполнении возможны два варианта, и все платежи для каждого из них представлены в таблице:

                                  Повышение                 Понижение

Поступления от продажи актива        2 х 120 = 240                       2 х 90 = 180

Платежи по короткой колл-позиции       3 х (-20) = -60                     3 х (0) = О

Возврат долга                                               -180                                    -180

Чистый поток наличности                                0                                         0

Платежи по портфелю, составленному из опционов и основных активов

Мы видим, что эта специально подобранная комбинация основных активов, займа и опционов приводит к одним и тем же финансовым результатам и при повышении цены основных активов, и при ее понижении. Таким образом, мы имеем безрисковый хедж. Коль скоро итоговая ценность полученного портфеля всегда равна нулю, его справедливая цена при формировании также должна быть нулевой. Следовательно, ЗС- 36.36 = 0 и С= 12.12.

Итак, мы нашли справедливую цену опциона на рисковый актив за единицу времени до момента исполнения. Единственные сведения, которые нам для этого потребовались, — это величины, на которые может увеличиться или уменьшиться цена, а также безрисковая процентная ставка. Удивительно, что при этом не требуется знать вероятности повышения или понижения цены.

Мы проиллюстрировали понятие безрискового опционного хеджа на конкретном примере, но сама эта техника имеет универсальный характер. В общем случае рассмотрим портфель, включающий:

a) продажу одного колл-опциона,

b) покупку h единиц основных активов,

c) займа в размере В.

Величины h и В нужно подобрать так, чтобы финансовый результат портфеля при исполнении опциона был нулевым как при увеличении, так и при уменьшении цены основных активов. Для этого должны выполняться равенства:

huS -- Cup ---BR =0,

hdS – Cdown ---BR=0,

где R = еit, i — непрерывно начисляемая сложная безрисковая процентная ставка, Сuри Cdown — стоимости опциона при исполнении в случаях повышения и понижения цен. Получилась система из двух уравнений с двумя неизвестными, и с помощью несложных алгебраических действий можно найти ее решения:

h = (Сuр – Cdown) / [S(u-d)] и B = (dСuр –u Cdown) / [R(u-d)] .                      (1)

Равенство нулю начального потока наличности означает, что

C-hS+B=0.

Подставляя сюда выражения для h и В, получим:

C = [(R-d)Сцр –(u-R) Cdown] / R(u-d).

И, наконец, после замены

p = R-d / u-d

получаем немного более удобное выражение для цены однопериодного опциона:

C = [pСuр –(1-p) Cdown] / R.                                                                              (2)

Величины р и (1 -р) выглядят как вероятности, поскольку их значения всегда попадают в отрезок от нуля до единицы, а полученное соотношение можно интерпретировать следующим образом: в любой момент времени стоимость опциона равна текущему значению среднего итогового результата, если при вычислении среднего каждый возможный результат берется с весом, равным вероятности его появления.

Посмотрим, что дают эти уравнения в рассмотренном выше конкретном примере:

h = (20 – 0) / (100(1.20—0.90)) = 0.6667, B = (0.90 x 20 – 1.20 x 0) / (1.10 x (1.20 – 0.90)) = 54.55

и,следовательно,

С =hS- В =0.6667х100 -54.55 =12.12.

Этот метод оценивания однопериодных опционов легко распространить на опционы с более длинными сроками. Рассмотрим, например, случай двухпериодного опциона. На следующем рисунке рассмотренный ранее пример продолжен еще на один шаг. Здесь, по-прежнему, начальная цена равна 100, и = 1.20, d = 0.90. Если цена на каждом из двух шагов будет расти, то в итоге она будет равна 100 х 1.20 х 1.20 = 144. Аналогично, если на каждом шаге она будет падать, то в итоге окажется равной 81. Если, наконец, цена сначала поднимется, а затем опустится, или наоборот, то в итоге она будя равна 108.

Чтобы оценить двухшаговый опцион, можно разбить полную задачу на несколько более простых задач (метод “разделяй и властвуй”). Начнем с верхней правой части диаграммы данного рисунка и изобразим ее отдельно на следующем рисунке.

Рис. Двухшаговая биномиальная схема оценки опциона.

Верхняя правая ветвь

Эта подзадача по сути полностью совпадает с задачей для одношагового опциона. При помощи соотношений (1) и (2) находим коэффициент хеджирования h и величину Сuр — они равны 1 и 29.09, соответственно. Аналогично поступаем с правой нижней частью рассматриваемого рисунка, получая при этом коэффициент хеджирования 0.30 и Cdown = 4.85. Мы нашли значения цены опциона за один шаг до исполнения. Осталось только подставить полученные числа в предыдущий рисунок и обработать левую часть диаграммы— она изображена отдельно на следующем рисунке:

Рис. Двухшаговая биномиальная схема оценки опциона.

Левая часть диаграммы

Это — опять-таки задача оценки одношагового опциона. Применив еще раз предыдущие формулы, получим коэффициент хеджирования 0.81 и цену опциона 19.10. На следующем рисунке показана вся двухшаговая схема целиком со всеми числовыми значениями.

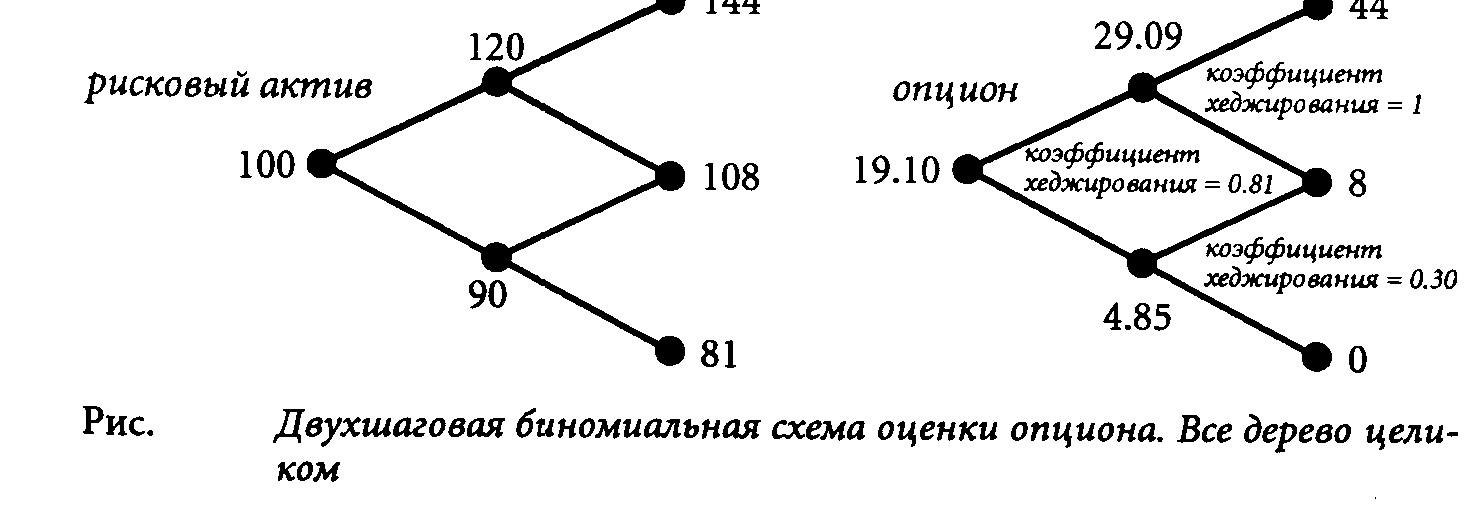
В решетке, описывающей двухшаговую модель, имеется три вершины, в которых цена может подняться или опуститься. Для каждой из этих вершин с помощью соотношения (1) определяется безрисковый хедж из опциона и основного актива. Коэффициент хеджирования может меняться от вершины к вершине. Это существенное свойство биномиальной модели, и в нем отражена реальна! практика финансистов, которые при хеджировании портфеля опционов постоянно уравновешивают хеджирующий портфель, чтобы поддерживать нейтрализацию риска. В двухшаговом примере, представленном на последнем рассмотренном рисунке, для хеджирования опциона нужно взять 0.81 основных активов. Если цена активов затем понизится, то следует продать 0.51 основных активов, чтобы уменьшить коэффициент хеджирования до 0.30. Наоборот, если цена активов возрастет, следует докупить их в количестве 0.19, доведя этим коэффициент хеджирования до 1.

Аналогично тому, как мы распространили одношаговую модель на два шага, можно продолжить ее на любое количество шагов. При этом получится "конусообразная" решетка типа тех, которые мы рассматривали, но длиннее. Каждая вершина решетки соответствует цене основных активов в некоторый момент времени. На каждом шаге цена может подняться или опуститься. Начиная с текущей рыночной цены в крайней левой точке, решетка постепенно расширяется, охватывая все возможны значения, которые с течением времени может принимать цена основных активов. Чем больше времени до исполнения опциона и чем больше волатильность основных активов, тем более широкой буде решетка.

Числа на узлах решетки можно получить в результате следующей последовательности действий:

1) Начать с левой точки решетки цен активов.

2) Заполняя решетку слева направо, последовательно находить значения цены основных активов, умножая предыдущие значения либо на и, либо на d.

3) Для каждой итоговой цены основных активов найти стоимость опциона в момент исполнения.

4) Далее заполнять справа налево решетку цен опциона, применяя всякий раз соотношение (2) (т.е. одношаговую модель оценки опциона).

5) Полученное в результате значение стоимости опциона в начальной точке решетки является его справедливой ценой в момент заключения опционного контракта.

В данном примере при помощи 10-шаговой биномиальной модели можно найти, что искомая справедливая цена опциона должна быть равна цене из. модели Блэка-Шоулса. Это говорит о том, что биномиальная модель, по-видимому, состоятельна. На практике, однако, обычно берут больше 10 шагов, потому что иначе ответ, который выдаст биномиальная модель, не будет вполне надежным (конечно, имеется в виду то, что в реальности котировки вряд ли ведут себя как в биномиальной модели, но увеличение шагов позволяет получить похожее поведение). На следующем рисунке представлены результаты, полученные по биномиальным моделям с различным числом шагов — от 1 до 100. Во многих коммерческих программных продуктах, основанных на этой модели, число шагов берется порядка 50— это дает удовлетворительный компромисс между надежностью и временем счета.

Биномиальная модель обладает достаточной гибкостью, позволяющей работать с основными активами, цены на которые соответствуют любому заданному распределению доходности. Нужный закон изменения цен можно обеспечить за счет выбора подходящих значений для и и d, причем в разных частях решетки они могут быть разными. Обычно и и d выбираются так, чтобы биномиальная модель аппроксимировала соответствующее практике логарифмически нормальное распределение цен.

Теперь мы попробуем оправдать сделанное в начале этого пункта предположение о том, что цена на каждом шаге может повыситься или понизиться только на строго определенную свою долю. Все наше обсуждение биномиальной модели основывалось на этом предположении. На первый взгляд, оно может показаться нереалистичным, однако теперь мы видим, что если шаги достаточно малы и их достаточно много, то за продолжительное время цена может меняться в широких пределах. Таким образом, сделанное в начале этого раздела предположение является вполне разумным, если величины отдельных шагов малы.

При неограниченном увеличении числа шагов биномиальной модели она в пределе совпадает с моделью Блэка-Шоулса. В связи с этим возникает вопрос: зачем вообще нужно пользоваться биномиальной моделью, связанной с вычислительно громоздким итерационным процессом? Ответ заключается в том, что биномиальная модель применима при минимальных ограничениях. С ее помощью можно оценивать такие опционы, к которым модель Блэка-Шоулса применить трудно. Например, для оценивания опционов американского типа или опционов на акции с нерегулярно выплачиваемыми дивидендами требуется вводить в модель Блэка-Шоулса существенные усложнения. В таких случаях биномиальная модель может оказаться наиболее простым методом.