3. План полного факторного эксперимента

№ опыта	Факторы			Значения отклика в повторных опытах		Выборочное среднее отклика
i
1	1	1	1	2,41	2,25	2,33
2	1	1	-1	2,29	2,28	2,285
3	1	-1	-1	2,29	2,25	2,27
4	1	-1	1	2,42	2,45	2,435
5	-1	1	-1	2,26	2,25	2,24
6	-1	1	1	2,25	2,23	2,24
7	-1	-1	1	2,27	2,24	2,255
8	-1	-1	-1	2,29	2,28	2,285

Данный план является полным, т.к. обладает следующими свойствами:

• Алгебраическая сумма элементов вектора-столбца каждого фактора равна нулю. Данное свойство называется симметричностью плана:

• Сумма почленных произведений любых двух векторов-столбцов равна нулю:

• Сумма квадратов элементов столбца каждого фактора равна количеству опытов N:

Построение квазилинейной регрессионной модели

Построим квазилинейную статистическую (регрессионную) модель вида:

Для нахождения коэффициентов a_m модели воспользуемся свойствами вектор-столбцов полного факторного эксперимента. Это позволит вычислить их по формулам:

; ;

Получили модель:

Перейдём от нормированных значений факторов к их натуральным значениям:

Выполнение критериальных проверок

Проверим значимость коэффициентов полученной квазилинейной модели с целью исключения из модели факторов, слабо влияющих на функцию отклика. Коэффициент считается значимым, если он значимо отличается от нуля в смысле критерия Стьюдента.

При количестве опытов в плане 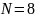и количестве повторных опытов число степеней свободы равно Выбираем доверительную вероятность и определяем по таблице из приложения 1 значение .

Дисперсия наблюдения

Доверительный интервал коэффициентов аl модели

Так как все коэффициенты квазилинейной модели больше доверительного интервала, все они являются значимыми.

Задание №3. Планирование эксперимента. Построение нелинейных уравнений регрессии. План № 60/9

Особенности плана: композиционный, симметричный, трехуровневый.

«Ядро» плана представляет собой полный факторный эксперимент , «звездное плечо» выбрано из условия минимизации определителя ковариационной матрицы.

Количество опытов в плане N = 24, количество повторных опытов в каждой точке плана n = 3, количество факторов M = 4.

Характеристика плана: – D – эффективность; – А - эффективность; - Е - эффективность; – Q – эффективность.

Квазилинейная модель имеет вид:

Из ковариационной матрицы С определяем

Оптимальны план эксперимента таблица 4

№ Опыта i	X1	X2	X3	X4	Y1	Y2			Y3		Среднее
1	-	-	-	-	34		36	39		36,33
2	-	-	-	+	35		33	37		35
3	-	-	+	-	32		34	36		34
4	-	-	+	+	42		40	45		42,33
5	-	+	-	-	46		41	44		43,67
6	-	+	-	+	45		43	42		43,33
7	-	+	+	-	35		33	31		33
8	-	+	+	+	32		36	38		35,33
9	+	-	-	-	34		37	32		34,33
10	+	-	-	+	30		35	33		32,67
11	+	-	+	-	28		31	26		28,33
12	+	-	+	+	39		34	37		36,67
13	+	+	-	-	46		48	50		48
14	+	+	-	+	34		35	32		33,67
15	+	+	+	-	47		45	43		45,00
16	+	+	+	+	30		32	34		32
17	+	0	0	0	25		29	27		27
18	-	0	0	0	26		29	31		28,67
19	0	+	0	0	32		33	29		31,33
20	0	-	0	0	28		24	26		26
21	0	0	+	0	24		27	22		2433
22	0	0	-	0	35		37	39		37,00
23	0	0	0	+	27		23	25		25
24	0	0	0	-	28		26	30		28

Коэффициенты модели вычислим по следующим формулам:

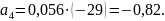
Получили модель: