Интеграл от функции комплексного переменного

Рассмотрим однозначную функцию , определенную и непрерывную в области . Пусть - кусочно-гладкая дуга линии, которая целиком принадлежит области ; дуга ограничена точками (начальная) и (конечная). Разделим дугу на элементарных дуг, занумеруем точки деления в направлении от точки до конечной точки , причем . Введем обозначения: , . На каждой элементарной дуге выберем одну точку (один из концов или внутреннюю точку) и запишем сумму

Интегралом от функции по дуге называется конечный предел суммы при

Интеграл от функции комплексной переменной имеет следующие свойства.

1.

2.

3. Если дуга геометрически совпадает с дугой , но имеет направление, противоположное направлению дуги (для начальная точка , а конечная ) , то

.

4. Если дуга состоит из дуг , то

5.

6. Если во всех точках дуги и длина дуги равна , то

7.

Вычисление интеграла

Вычисление интеграла от однозначной функции комплексной переменной сводится к вычислению обычных криволинейных интегралов

Интеграл вообще говоря зависит от пути интегрирования .

Если - аналитическая функция в односвязной области , то значение интеграла не зависит от линии , а только от начальной и конечной точки этой линии.

Теорема Коши.

Для всякой функции , аналитической в некоторой односвязной области , интеграл по любому кусочно-гладкому замкнутому контуру , целиком принадлежащему области , равен нулю

Если кривая задана параметрическими уравнениями , , , то

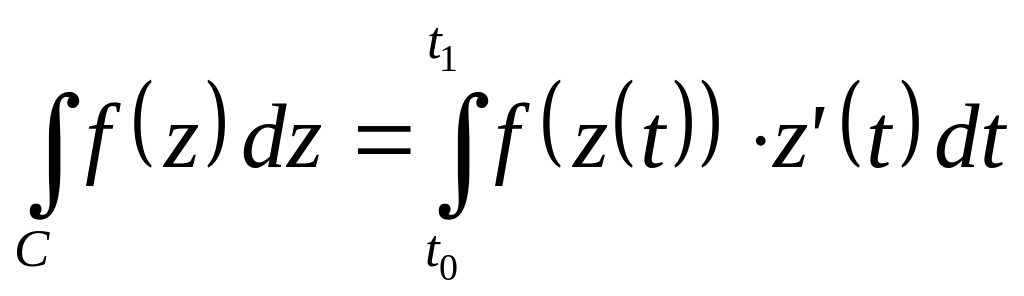
где .

Если функция аналитическая в однозначной области , содержащей точки и , то справедлива формула Ньютона-Лейбница

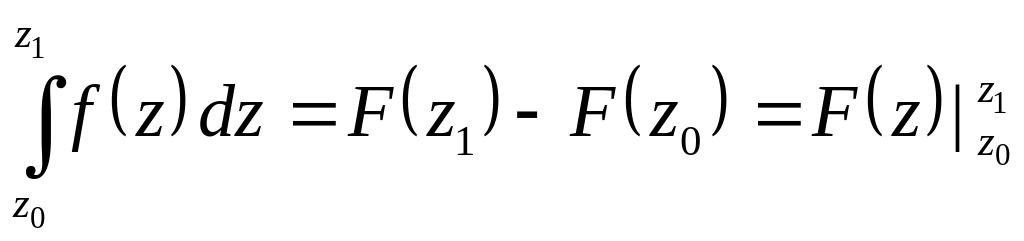
Если функции и - аналитические в односвязной области , а и - произвольные точки этой области, то справедлива формула интегрирования по частям

Пример. Вычислить интеграл , где 1. линия - отрезок действительной оси, соединяющей точки , , 2. - верхняя полуокружность .

Поскольку для комплексного числа сопряженным является число , то на действительной оси , и . Поэтому в первом случае

2. Верхнюю полуокружность можно задать так. , где , причем убывает. Поскольку , , то

Интегральная формула Коши

Если функция является аналитической в области , ограниченной кусочно-гладким контуром , и на самом контуре, то верна интегральная формула Коши

где - любая точка внутри контура и контур обходится так, чтобы область все время оставалась слева (обход контура против часовой стрелки).

Таким образом, аналитическую функцию достаточно определить на контуре , а по этой формуле можно автоматически получить ее значения в других точках .

Если функция аналитическая в области и на ее границе , то для любого натурального верна формула

- значение производной функции в точке .

Это позволяет вычислить следующие интегралы

Пример. Вычислить интеграл , где - окружность радиуса с центром в точке , причем обход контура осуществляется против часовой стрелки.

Преобразуем подынтегральную функцию следующим образом

Функция является аналитической внутри рассматриваемого круга и на его границе. Поэтому запишем

Степенные ряды. Ряд Тейлора.

Функция , однозначная и аналитическая в точке , разлагается в окрестности этой точки в ряд Тейлора

коэффициенты которого определяются формулами

где - окружность с центром в точке , расположенная в окрестности точки , в которой функция аналитическая. Центр окружности круга сходимости находится в точке ; эта окружность проходит через особую точку функции , ближайшую к точке , т.е. радиус сходимости ряда будет равен расстоянию от точки до ближайшей особой точки функции .

Для функций , , , ряд Тейлора имеет следующий вид:

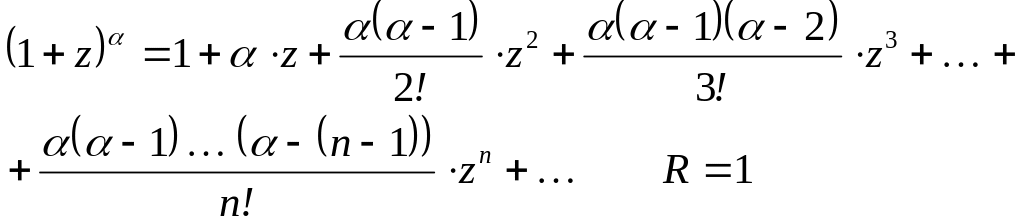
Пример. Разложить в ряд Тейлора функцию в окрестности точки .

Преобразуем эту функцию следующим образом . Поскольку , то при получим

Следовательно,

Полученный ряд сходится при , или .