20 Тфкп Комплексные числа.

Комплексное число записывается в виде

где - действительные числа, - мнимая единица .

Комплексные числа записывают также в тригонометрической форме

где, соответственно

. Комплексно сопряженная форма комплексного числа - .

Действия над комплексными числами

Сложение и вычитание

Умножение

Деление

Возведение в степень

Извлечение корня

Примеры:

Понятие функции комплексного переменного

К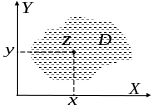 омплексное число имеет вид , где и - действительные числа, - мнимая единица . Оно изображается точкой на комплексной плоскости с координатами . Пусть - область (открытое связанное множество) комплексной плоскости . Если каждой точке по определенному правилу поставлено в соответствие единственное комплексное число , то говорят, что в области определена однозначная функция комплексной переменной и пишут . Функцию можно рассматривать как комплексную функцию двух действительных переменных и , определенную в области . Задание такой функции равносильно заданию двух действительных функций , , . Таким образом, если , , то

Комплексное число является пределом однозначной функции при , если для всякого существует такое число , что из неравенства следует неравенство . В этом случае пишут .

Функция называется непрерывной в точке , если

Функция, непрерывная в каждой точке области , называется непрерывной в этой области.

Область называется односвязной, когда она ограничена замкнутой линией , не пересекающей себя. Область называется двусвязной, когда она ограничена двумя замкнутыми линиями и , которые не пересекаются и каждая не пересекает себя; внутренняя линия , в частности, может вырождаться в точку или в дугу непрерывной линии. Аналогично определяется трехсвязная, четырехсвязная и т.д. области.

П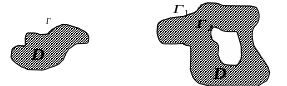 ример. Найти значение функции при следующих значениях аргумента: 1. , 2. , 3. .

Элементарные функции комплексной переменной

Функции комплексной переменной , , определяются как суммы соответствующих степенных рядов, сходящихся на всей комплексной плоскости:

Показательная функция имеет следующие свойства: 1. , где - произвольные комплексные числа, 2. , т.е. является периодической функцией с периодом .

Тригонометрические функции , - периодические с действительным периодом ; они имеют только действительные нули и соответственно, где .

Для функций , , справедливы формулы Эйлера

откуда

Если , то , поэтому

Тригонометрические функции , определяются формулами

,

Все формулы тригонометрии остаются справедливыми и для тригонометрических функций комплексной переменной.

Гиперболические функции , , , определяются формулами

, , ,

Функции , можно рассматривать как суммы степенных рядов, сходящихся на всей комплексной плоскости:

Тригонометрические и гиперболические функции связаны между собой следующими равенствами

Логарифмическая функция , где , определяется как функция, обратная показательной, причем

Эта функция является многозначной. Главным значением называется такое значение, которое получается при , оно обозначается через :

Очевидно, что

Справедливы следующие равенства

Обратные тригонометрические функции , , , определяются как функции, обратные тригонометрическим функциям , , , . Например, когда , то называется арксинусом числа и обозначается .

Все эти функции являются многозначными, они выражаются через логарифмические функции следующими формулами

Главные значения обратных тригонометрических функций , , , получаются, когда рассматриваются главные значения соответствующих логарифмических функций.

Общая степенная функция , где - любое комплексное число, определяется формулой

ее главное значение равно

Общая показательная функция ( - любое комплексное число) определяется формулой

главное значение этой многозначной функции равно

Пример. Найти . Используя формулу для - , получим