
- •Решение вычислительных задач на компьютере
- •Точность вычислений
- •П огрешности измерений
- •П огрешности вычислений
- •Решение уравнений Приближенные методы
- •М етод перебора
- •Метод деления отрезка пополам
- •Пример: полет мяча
- •Использование табличных процессоров
- •Дискретизация в ычисление длины кривой
- •Вычисление площадей фигур
- •Оптимизация Что такое оптимизация?
- •Локальные и глобальный минимумы
- •Метод дихотомии
- •Пример: оптимальная раскройка листа
- •Использование табличных процессоров
- •Статистические расчеты
- •Свойства ряда данных
- •Условные вычисления
- •Связь двух рядов данных
- •Обработка результатов эксперимента
- •Зачем это нужно?
- •Метод наименьших квадратов
- •Восстановление зависимостей
- •Прогнозирование
Оптимизация Что такое оптимизация?
Оптимизация – это поиск наилучшего (оптимального) решения задачи в заданных условиях. |
С точки зрения математики, цель оптимизации – выбрать неизвестную величину x (или несколько неизвестных величин – массив) наилучшим образом.
Чтобы задача оптимизации была корректной, нужно определить целевую функцию , которая позволяет сравнивать два решения. Оптимальным называется такое решение, при котором целевая функция достигает максимума (если это «доходы», «прибыль») или минимума («расходы», потери»):
![]() или
или
![]() .
.
Чтобы задача оптимизации стала осмысленной, нужно ввести ограничения. Например, человек хочет построить загородный дом за минимальную цену (здесь целевая функция – это общая цена строительства, нужно сделать ее минимальной). Очевидно, что лучшее решение – не строить дом вообще, при этом расходы будут равны нулю. Такое «оптимальное» решение получено потому, что мы не задали ограничения (например, нужен двухэтажный дом с гаражом, балконом и камином).
Локальные и глобальный минимумы
По
традиции в теории оптимизации рассматривают
задачу поиска минимума. Если нужно найти
максимум, просто меняют знак функции:
значение функции
максимально там, где значение функции
![]() минимально.
минимально.
В
математике различают локальный
(«местный») и глобальный
(«общий») минимум. В точках
![]() ,
,
![]() и
и
![]() функция, график которой показан на
рисунке, имеет локальные
минимумы, этот значит,
что слева и справа от этих точек функция
возрастает.
функция, график которой показан на
рисунке, имеет локальные
минимумы, этот значит,
что слева и справа от этих точек функция
возрастает.


Минимум в точке – глобальный, потому что здесь функция имеет наименьшее значение во всей рассматриваемой области.
Очевидно, что нас всегда интересует глобальный минимум. Однако большинство существующих методов оптимизации2 предназначены именно для поиска локальных минимумов вблизи заданной начальной точки (начального приближения). Можно представить себе, что график функции – это срез поверхности, на которую устанавливается шарик в некоторой начальной точке; куда этот шарик скатится, такой минимум и будет найден.
Результат оптимизации зависит от выбранного начального приближения. |
Метод дихотомии
Дихотомия (греч. διχοτομία – «деление надвое») – это метод поиска минимума функции, который очень напоминает метод деления отрезка пополам (бисекции). Пусть дана непрерывная функция , имеющая на отрезке один минимум в точке . Нужно найти это значение с заданной точностью .


Как и в методе бисекции, мы последовательно «сжимаем» отрезок, пока его ширина не будет достаточно мала (меньше, чем ). На каждом шаге
вычисляется середина интервала ;
вычисляются координаты двух точек, симметричных относительно середины:
 и
и
 ,
где
,
где
 – некоторое число;
– некоторое число;сравниваются значения функции в этих точках: если
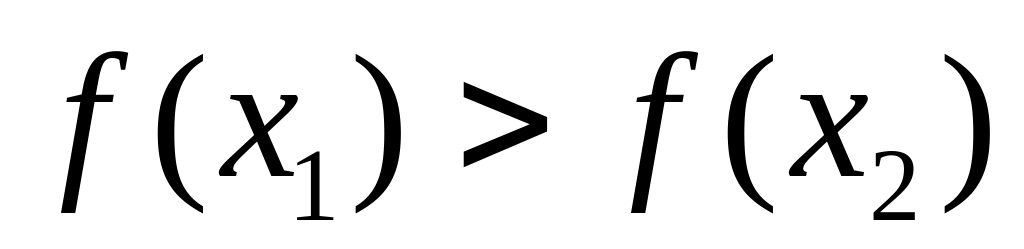 минимум функции находится на отрезке
минимум функции находится на отрезке
 ,
поэтому отрезок
,
поэтому отрезок
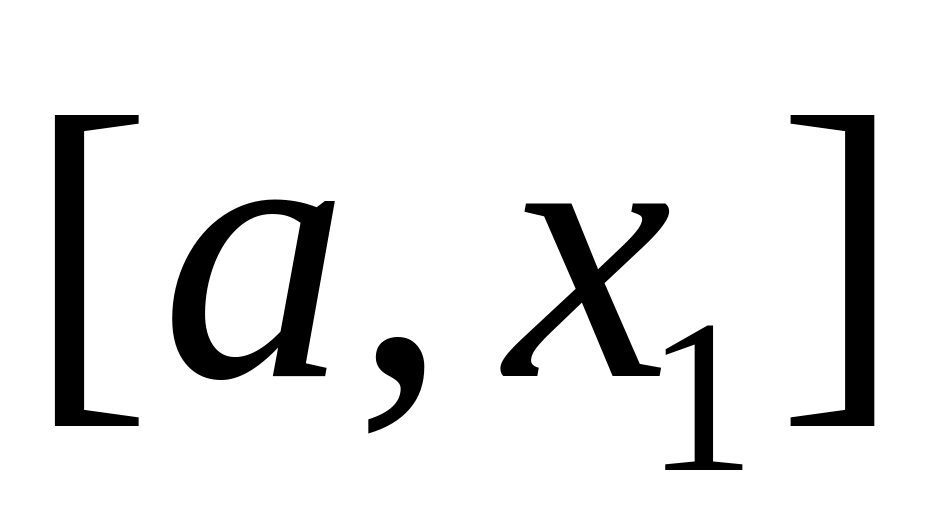 можно отбросить – переместить левую
границу в точку
можно отбросить – переместить левую
границу в точку
 ;
если
;
если
 правая граница интервала перемещается
в точку
правая граница интервала перемещается
в точку
 .
.
Остается
один вопрос: как выбирать
![]() на каждом шаге? Проще всего вычислять
его по формуле
на каждом шаге? Проще всего вычислять
его по формуле
![]() ,
где
,
где
![]() – постоянный коэффициент (
– постоянный коэффициент (![]() ).
Тогда ширина интервала на следующем
шаге будет равна
).
Тогда ширина интервала на следующем
шаге будет равна
![]() ,
,
то
есть составит
![]() от первоначальной. Для ускорения поиска
выгодно, чтобы это отношение было как
можно меньше, то есть чтобы коэффициент
был возможно ближе к нулю (ноль выбирать
нельзя, потому что при этом точки
и
совпадут и метод не будет работать).
Программа может выглядеть примерно
так:
от первоначальной. Для ускорения поиска
выгодно, чтобы это отношение было как
можно меньше, то есть чтобы коэффициент
был возможно ближе к нулю (ноль выбирать
нельзя, потому что при этом точки
и
совпадут и метод не будет работать).
Программа может выглядеть примерно
так:
k:= 0.01; delta:= 2*eps; нц пока b - a > delta r := k*(b - a); x1 := (a + b)/2 - r; x2 := (a + b)/2 + r; если f(x1) > f(x2) то a := x1 иначе b := x2; все кц вывод 'Решение ', (a+b)/2; |
k := 0.001; delta := 2*eps; while b - a > delta do begin r := k*(b - a); x1 := (a + b)/2 - r; x2 := (a + b)/2 + r; if f(x1) > f(x2) then a := x1 else b := x2; end; writeln('Решение: ', (a+b)/2:10:3 ); |
В качестве упражнения можно исследовать работу этой программы при разных значениях , подсчитав для каждого варианта количество шагов цикла, которое потребовалось для получения решения с заданной точностью.
Существует вариант метода дихотомии, при котором на каждом шаге цикла нужно вычислять только одно значение функции (второе «переходит» с предыдущего шага). В этом случае нужно выбирать коэффициент равный отношению «золотого сечения»:
![]()
