Восстановление зависимостей

Пусть заданы пары значений и , и предполагается, что они связаны некоторой зависимостью , которую нужно найти. Такая задача называется задачей восстановления зависимости.

Если вид функции не задан, эта задача некорректна, потому что через заданные точки можно провести сколько угодно различных линий (графиков функций), и невозможно сказать, какая из них лучше подходит:

Поэтому для того, чтобы сделать задачу осмысленной нужно заранее задать вид функции, так что останется только найти ее неизвестные коэффициенты.

Откуда взять вид функции? В некоторых случаях он известен из физических законов, описывающих явление (так было в примере с исследованием закона Гука). Иногда вид зависимости можно определить по внешнему виду расположения точек. Также можно попробовать функции разного типа и выбрать лучший вариант. Часто используют следующие типы функций:

• л инейную ;

• логарифмическую ;

• показательную (экспоненциальную) ;

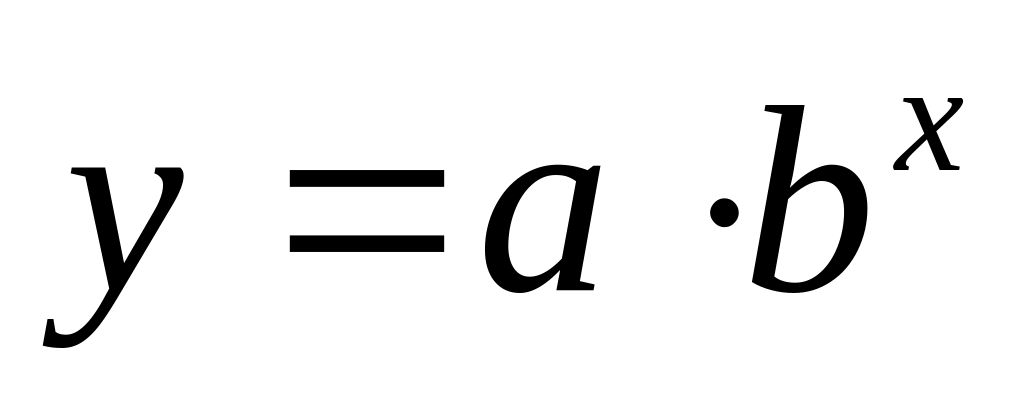• степенную .

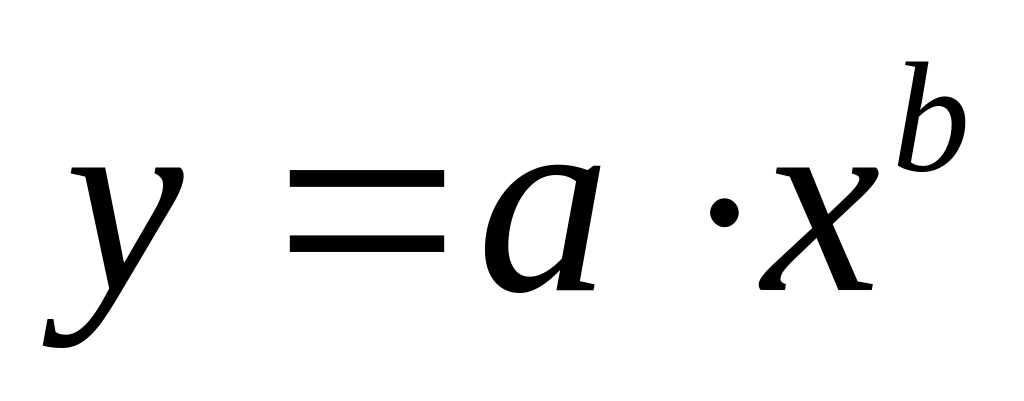Задача сводится к тому, чтобы выбрать коэффициенты и наилучшим образом. Для ее решения «вручную» нужно применять методы вычислительной математики, выходящие за рамки школьного курса. Однако в современных табличных процессорах есть встроенные возможности для решения задачи восстановления зависимостей. Полученные графики оптимальных функций называются линиями тренда (англ. trend – основное направление развития).

Сначала нужно ввести исходные данные (координаты точек) в таблицу и построить по ним диаграмму типа «Диаграмма XY» (в Excel – «Точечная»). Лучше оставить на диаграмме только точки, не соединяя их линией.

Для того, чтобы построить линию тренда, надо щелкнуть правой кнопкой мыши на одной из точек и выбрать пункт «Вставить линию тренда» из контекстного меню. В появившемся окне можно выбрать вид зависимости. Если установить флажок «Показать уравнение», уравнение линии тренда будет показано на диаграмме. Флажок «Показать коэффициент детерминации (R²)» позволяет увидеть, насколько точно полученная линия соответствует исходным данным. Коэффициент R² вычисляется по формуле:

,

где через обозначено среднее значение ряда . Этот коэффициент всегда не больше 1 (подумайте, почему), чем он больше, тем лучше соответствие. В лучшем случае , при этом для всех i , то есть все значения функции совпадают с заданными.

Из приведенной формулы видно, что имеет наибольшее значение, когда сумма квадратов отклонений минимальна. Это значит, что задача поиска максимума решается методом наименьших квадратов. Если нужно найти неизвестные коэффициенты функции, которая не входит в стандартный набор (например, ) можно применить метод наименьших квадратов с помощью надстройки «Поиск решения».

Прогнозирование

Во многих задачах (например, в экономике) в результате обработки данных нужно сделать прогноз на будущее. Если найдена зависимость , эта задача решается просто – нужно найти значения функции для тех значений , которые нас интересуют. Однако может получиться так, что функция, которая очень хорошо соответствует имеющимся данным (см. функцию на рисунке), оказывается непригодна для прогноза:

В таких случаях для решения задачи прогнозирования нужно выбирать другую функцию, которая дает меньшее значение , но лучше показывает закономерность изменения величины (например, возрастающий характер функции).

1. Объясните, почему экспериментальные исследования требуют специальных методов обработки данных.

2. Объясните суть метода наименьших квадратов. Почему можно считать такой подход решением задачи оптимизации?

1. Результаты серии измерений, сделанных для определения жесткости пружины на основе закона Гука, записаны в таблицу:

, Н	1	3	6	10
, м	0,028	0,070	0,170	0,260

Используя метод наименьших квадратов, определите жесткость пружины. Решите задачу разными способами (с помощью собственной программы и табличного процессора), сравните результаты.

2. *Используя те же данные, что и в предыдущей задаче, найдите жесткость пружины другим способом. Введем величину, обратную жесткости: 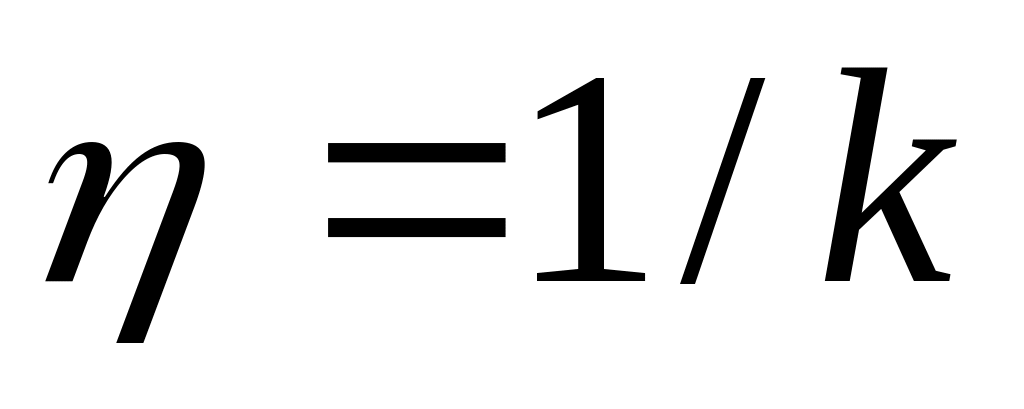, тогда . Сначала, применив метод наименьших квадратов, найдите , а затем рассчитайте 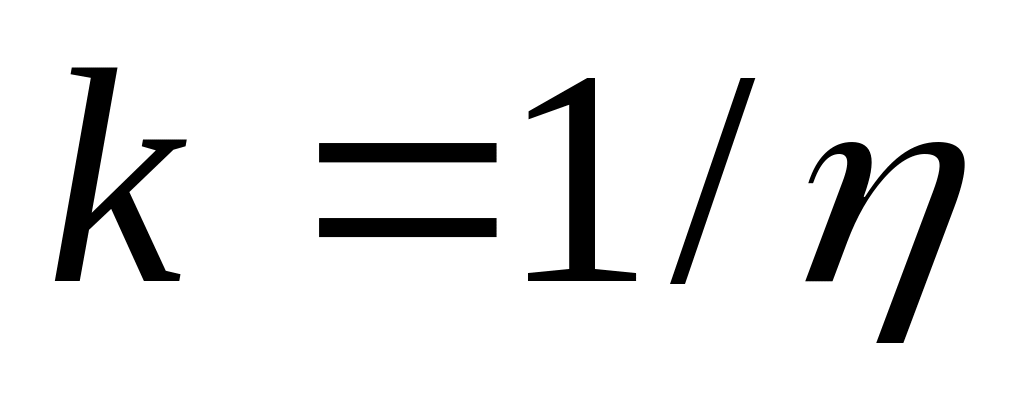. Сравните результат с тем, что получилось в предыдущем задании. Объясните расхождение.

3. Почему задача восстановления зависимости некорректна, если не задан вид функции?

4. Доходы начинающей фирмы (в тысячах рублей) за первые 5 лет работы приведены в таблице:

Год	1	2	3	4	5
Доход	93	187	270	321	350

С помощью табличного процессора найдите зависимость дохода от года работы (выберите лучший из стандартных вариантов, с наибольшим значением ). С помощью этой зависимости сделайте прогноз развития фирмы на 2 года вперед.

5. *При изучении волн измерили отклонение уровня поверхности воды y от «нулевого» уровня в одной точке в разные моменты времени t:

t	0	0,2	0,4	0,6	0,8	1
y	1	2	1,2	-0,6	-2	-1,5

Предполагается, что волна описывается формулой , где , и – некоторые числа. Определите неизвестные коэффициенты методом наименьших квадратов с помощью табличного процессора. В качестве начального приближения можно выбрать ; ; .

Самое важное в главе 9: Погрешность вычислений – это разница между вычисленным значением величины и её точным (истинным) значением. Точность вычислений определяется точностью исходных данных и погрешностями метода. Компьютер позволяет легко находить приближенные решения многих задач, которые трудно решаются аналитически (или не решаются вообще). Задача вычислительной математики – повысить точность и увеличить скорость компьютерных вычислений. Дискретизация – необходимый этап подготовки вычислительных задач для решения на компьютере. Оптимизация – это поиск наилучшего решения в заданных условиях.

1 Хотя можно, например, использовав замену .

2 Для некоторых типов функций существуют методы глобальной оптимизации, но они, как правило, сложны и выходят за рамки школьного курса.

3 Задачи 3 и 4 предложены В.Я. Лаздиным.

4 Попробуйте доказать это самостоятельно.

http://kpolyakov.narod.ru