3. Есеп шығаруға қойылатын негізгі талаптар

Есеп шығаруға төмендегідей талаптар қойылады:

а) Қатесіз шығару; ә) негіздеу (дәлелдеу), б) толық шығару; в) мүмкіндігінше тиімді жолмен шығару; г) есепті қаттау (оформление).

а) “Есеп қатесіз шығарылу керек”.

Бұл негізгі талап. Оқушылар есеп шығару кезінде алгоритмдік, логикалық, сызбалық, терминологиялық, шындықты бұрмалау сияқты қателер жіберуі мүмкін. Енді оқушылар жиі жіберетін қателіктерді көрсетелік.

– алгоритмдік қателіктер.

5=–5 екендігін дәлелдеу. Екі жағын квадраттаймыз, сонда 25=25

немесе

1=1 – логикалық қателік.

Бүйір жақтары квадраттар болатын алты бұрышты дұрыс призманың ішінен төменгі табанының қабырғасы мен жоғарғы табанының оған қарсы жатқан қабырғасы арқылы жазықтық жүргізіңдер. Осы қима тік төртбұрыш ретінде салынса, ол сызбалық қате.

“Бүйір жағының апофемасы”, “шеңбердің ауданы” т.с.с. – терминологиялық қателіктер.

Есеп: “Моторлы қайық өзен ағысымен 42 км және ағысқа қарсы 20 км жол жүріп және оған 5 сағ уақыт жұмсады. Егер өзен ағысының жылдамдығы 2 км/сағ болса, қайықтың өз жылдамдығы қандай?”.

Есеп теңдеуін құру арқылы шығарылды. Теңдеу түбірлері 2/5 және 12 есеп жауабы ретінде алынса, онда шындықты бұрмалау қателігі жіберілгені. Себебі, қайық жылдамдығы өзен жылдамдығынан артық болуы тиіс, яғни 2/5 есеп шартын қанағаттандырмайды. Жауабы: 12 км/сағ.

ә) Есеп шығару кезеңінің әр сатысы міндетті түрде негізделіп, дәлелденіп отыруы қажет. Яғни әрбір жаңа ой қорытындысы қандай тұжырымнан туындалады, не себепті олай деп пайымдауға хақымыз бар сұрақтарға мұқият жауап берілуі керек.

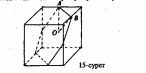
Мысал. Қыры а-ға тең кубтың төменгі табанының іргелес қабырғаларының ортасынан және жоғарғы табанының олармен бір жағында жатпайтын екі іргелес қабырғаларының орталары арқылы жазықтық жүргізіліген. Қиманың ауданын тап.

Шешуі:

шешуі дұрыс болғанмен, қимадағы алтыбұрыш неге дұрыс екендігін дәлелдеп көрсету керектігі туындайды (15-сурет).

Немесе “дұрыс үшбұрышты пирамиданың бүйір қырлары табан жазықтығымен өзара тең α бұрышын жасайды. Егер пирамиданың бүйір қыры b болса, онда оның биіктігі неге тең болатынын тап”.

Осы пирамиданың төбесі табанға қалай проекцияланатынын дәлелдемей есепті әрі қарай шығару туралы сөз болмағанда болар еді.

б) Теңдеудің бір шешімі дұрыс табылды делік, ал оның әлі екі шешімі бар. Бірден түсінікті, есеп толық шығарылған жоқ, немесе кейде иррационал теңдеулерді шешкенде бөгде түбірлер пайда болуы мүмкін. Егер табылған шешімдердің бәрін теңдеу түбірі десек, есеп толық шығарылмағаны. Зерттеулерге арналған есептерде (әсіресе, геометриялық) мүмкін болатын барлық жағдайлар қарастырылғанда ғана, есеп толық шығарылды деп айта аламыз.

в) Есеп мүмкіндігінше тиімді, ұтымды жолмен шығарылғаны жөн. Мысал ретінде 11-сынып геометриясындағы (А.В.Погорелов) есепті қарастырайық. “Үшбұрышты пирамиданың бүйір қырлары өзара перпендикуляр, олардың әрқайсысы b-ға тең. Пирамида көлемін табыңдар” (16-сурет).

Берілгені:

Табу керек: V_{пирамида} – ?

Шешуі: Пирамиданы аударып, табаны ретінде SBC үшбұрышын қарастырсақ, есеп әлдеқайда оңай шығарылады:

Мысал. теңсіздігінің шешімін табу ұсынылса, әдетте

шығару былай жүргізіледі:

одан әрі интервалдар әдісі қолданылады. Есепті сызбалық тәсілмен шығару, тиімді жолдың бірі болар еді (17-сурет).

Жауабы: (-1;0) (1;+∞)

г) Есеп шығару кезеңдерін дұрыс қаттау да есепке жүктелетін талаптардың бірі болып саналады. Есеп шығару кезеңдері қысқа да нұсқалы, түсінікті, сызбалар қатесіз, дәл т.б. болуы қажет. Геометриялық есептер шығаруда есеп мазмұнына сәйкес ақылға қонымды сызба салынуы керек. Есеп шарттары, талабы айқын көрсетілуі тиіс. Шығару жолдары қысқа түрде, қажет символикаларды пайдаланып жазылуы керек. Әр жаңа тақырыпқа есептер шығарылғанда, мүмкін болатын жазу үлгісі беріліп, ілгеріде соның мұқият сақталуын қадағалаған жөн. Логарифмдік теңдеуді шығару кезеңдерінің жазу үлгісін ұсыналық:

Тексеру (1)

(1)-ге қойсақ, 1) – шын

2) – жалған

Жауабы: х=-1

Сұрақтар:

1. Есептің математиканы оқытудағы орны және міндеттері

2. Математикалық есеп және оның түрлері;

3. Есепті шығарға қойылатын талаптар

Пайданылған әдебиеттер

1.Әбілқасымова А. және т.б. Математиканы оқытудың териясы мен әдістемесі. А, Білім. 1998 ж

2. Бидосов Ә. Математиканы оқыту методикасы. (Жалпы методика). А, Мектеп. 1989ж

3. Рахымбек Д. және т.б. Орта мектепте математиканы оқыту әдістемесіне арналған оқу құралы. Ш, 2003