50. Элементар электр заряды. Электр зарядының сақталу заңы.
Элементар (минимал) электр
заряды дегеніміз 
Кл.
Теріс таңбалы элементар
зарядты тасушы – электрон.
Оның массасы 
кг.
Элементар оң таңбалы зарядты тасушы
– протон.
Оның массасы 
кг.
Тәжірибе жүзінде тағайындалған электр зарядының мынадай негізгі қасиеттері бар:
- Запрядтың екі түрі бар: оң және теріс. Аттас зарядтары тебіледі, әр аттас зарядтар тартылады.
- Электр заряды инвариантты – оның шамасы санақ жүйесіне байланысты емес, яғни ол қозғалады ма, әлде тыныштықта болады ма.
- Электр заряды дискретті – кез-келген дененің заряды элементар зарядқа бүтін еселі болады.
- Электр заряды аддитивті – кез-келген денелер жүйесінің заряды (бөлшек) осы жүйеге енетін денелер (бөлшектер) зарядының қосындысына тең.
- Электр заряды зарядтың сақталу заңына бағынады; кез-келген тұйық жүйедегі электр зарядының алгебралық қосындысы берілген жүйе ішінде қандай процесс жүрсе де өзгеріссіз қалады.
51. Кулон заңы. Электр тұрақтысы. Ортаның диэлектрлік өтімділігі. Кулон заңы
Нүктелік зарядтардың өзара
әсерлесуінің негізгі заңын, тәжірибе
жүзінде Кулон анықтады. Кулон заңын
тұжырымдамас бұрын нұктелік заряд
ұғымын енгіземіз (кинематикада енгізілген
материялық нүкте туралы түсінік сияқты)
нүктелік заряд дегеніміз – сызықтық
өлшемдері әсерлесуші зарядталған
денелердің ара қашықтығынан өте аз
болып келетін денеде орналасқан заряд.
Кулон заңы бойынша: вакуумда
орналасқан екі
және
нүктелік зарядтардың өзара әсерлесу
күшінің модулі олардың шамаларының
көбейтіндісіне тура, ал ара қашықтығының
квадратына кері пропорционал:
,
(11.1)
мұндағы
-өлшем
жүйесіне байланысты болатын пропорционалдық
коэфффициент. Зарядтар арсындағы бұл
күш осы зарядтар орналасқан түзу сызықтың
бойымен бағытталған, яғни орталық күш
болып табылады. Аттас зарядтар үшін (
және
немесе
және
)
,
ал зарядтар әр аттас болса,
болады. Векторлық түрде Кулон заңы былай
жазылады:
,
(11.2)
мұндағы
-
бірінші зарядқа екінші зарядтың әсер
етуші күші,
-
бірінші зарядтан екінші зарядқа
бағытталған радиус-вектор,
.
Бұл теңдеу аттас зарядтардың бірін-бірі
тебетіндігін, әр аттас зарядтардың
бірін-бірі тартатындығын көрсетеді.
Егер де әсерлесуші зарядтар вакуумда
емес, қандай да бір ортада орналасқан
болса, онда Кулон заңы былай жазылады:
,
(11.3)
мұндағы
-өлшем
бірлігі жоқ, ортаның электрлік қасиетін
көрсетуші диэлектрлік
өтімділікдеп
аталатын физикалық шама. Вакуум үшін
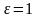болады. Жоғарыдағы (11.1) және (11.3)
теңдеулерінен
-нің
берілген ортадағы әсерлесуші күштің,
вакуумдағы әсерлесуші күшінен қанша
есе аз екенін көрсететінін байқау қиын
емес. Бірліктердің халықаралық жүйесінде
(БХЖ)
,
(11.4)
Бұл
формуладағы
)
немесе Ф/м
– электр
тұрақтысы
деп аталады. Осы (11.4) және (11.3) - теңдеулерге
сүйене отырып, Кулон заңын төмендегідей
жазуға болады:
.
(11.5)
мұндағы
екендігін айта кеткен жөн. Фарад (Ф) –
электр сыйымдылығының өлшем бірлігі.