61. Конденсаторларды қосу

Әрбір конденсатор тек өзінің сыйымдылығымен ғана емес, сонымен бірге максимал жұмыстық кернеуімен сипатталады. Егер конденсаторға жұмыстық кернеуден артық кернеу берілетін болса, онда конденсатор астарлары арасынан ұшқын шығып, конденсатор істен шығады. Бұл құбылыс конденсатордың тесілуі деп аталады. Берілген жұмыстық кернеу кезінде қалаған сыйымдылық алу үшін конденсаторларды тізбектей, параллель немесе аралас түрде қосады.

1)                                                         Конденсаторларды параллель қосу

Кондесаторларды параллель қосқан кезде барлық конденсаторлардағы кернеу бірдей болады: Конденсаторлар батареясындағы толық заряд

Конденсаторларды параллель қосқан кездегі батареяның толық электр сыйымдылығы келесі формуламен анықталады:

 

2) Конденсаторларды тізбектей қосу

Конденсаторларды тізбектей қосқан кезде барлық конденсаторлардағы зарядтар бірдей, конденсаторлар батареясының толық зарядына тең  болады:

Батареяларға түсірілген кернеу жеке конденсаторларға түсірілген кернеулердің қосындысына тең болады:

Конденсаторларды тізбектей қосқан кездегі батареяның толық электр сыйымдылығы келесі формуламен анықталады:

Конденсаторлар аралас қосылған кезде батареяның толық сыйымдылығы олардың қосылу схемасына тәуелді және параллель немесе тізбектей қосу заңдылықтарын пайдаланып анықтауға болады.

62. Зарядталған өткізгіш, зарядталған конденсатор, электростатикалық өріс энергиясы. Электростатикалық өріс энергиясының көлемдік тығыздығы. Зарядталған өткізгіштің энергиясы

заряды бар өткізгішті қарастырайық. Оны нүктелік зарядтар жүйесі ретінде қарастыруға болады. Жоғарыда N нүктелік зарядтар жүйесінің өзара әсерлесу энергиясы өрнегін жазғанбыз:

. (14.8)

Мұндағы - заряд орналасқан нүктедегі -ден басқа барлық зарядтардың тудырған потенциалы. Өткізгіштің беті - эквипотенциал бет. Сондықтан нүктелік зарядтар тұрған нүктелердің потенциалдары бірдей және өткізгіштің потенциалдарына тең болады. (14.8) формуласын пайдаланып, зарядталған өткізгіштің энергиясы үшін:

(14.9)

өрнегін аламыз. Төмендегі өрнектер кезкелген, зарядталған өткізгіштің энергиясын анықтайды:

. (14.10)

Зарядталған конденсатордың энергиясы

Енді жазық конденсатордың астарлары арасындағы біртекті өрісті қарастырайық. Мұндай конденсатордың зарядталу процесінде шексіз аз заряд біртіндеп бір пластинадан екінші пластинаға өтеді. Соның нәтижесінде бір пластина оң, ал екіншісі теріс зарядталады деп есептеуге болады және олардың арасында біртіндеп өсетін потенциалдар айырымасы пайда болады. Оңашаланған өткізгіш үшін дәлелденген қорытындыны қайталап, зарядталған конденсатордың толық электрстатикалық энергиясы үшін өрнекті жазуға болады:

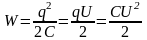, (14.3)

(14.3) өрнекке жазық конденсатордың сыйымдылығы мен потенциалдар айырымының мәндерін ( және ) қойсақ, түрлендірілгеннен кейін алатынымыз:

.

Электростатикалық өpic энергиясы. Электростатикалық өpicтe зарядты бip нүктеден екінші нүктеге көшірген кезде жұмыс жасалатынын білеміз. Бұл жұмыс өpicті тудырушы зарядтардың өзара әсерлесуін сипаттайтын потенциалдык энергия, болмаса сыртқы күштер есебінен жасалуы мүмкін. өзара әсерлесетін зарядтар системасының энергиясы бар. Бұл энергияны зарядтардың өзара әсерлесу энергиясы (зарядталған дененің әр түрлі бөліктерінің өзара әсерлесу энергиясы) түрінде, болмаса осы зарядтар тудыратын электр энергиясы түрінде жазуға болады.

. Бұл өрнек электр өрісі энергиясының тығыздығының өрнегі деп аталады. Электрлік ығысу векторының мәнін, яғни екенін ескеріп, тығыздықты басқа түрде өрнектеуге болады: .