12.3. Перелік рекомендованої літератури

1. Технологія наукових досліджень електроенергетичних систем в аграрному виробництві: Навчальний посібник./ Г.Б.Іноземцев, В.В.Козирський. За редакцією Г.Б. Іноцемцева. – К.: ТОВ «Аграр Медіа Груп», 2011. – 198 с.

2. В.М. Шейко, Н.М. Кушнаренко Організація та методика науково- дослідницької діяльності: Підручник. 3 – е вид., стер. – К.: Знання – Прес, 2003, - 295 с.

3. Крушельницька О.В. Методологія та організація наукових досліджень: навч. посібник / О. В. Крушельницька. - К.: Кондор, 2006. - 206 с

4. Пилипчук М.І. Основи наукових досліджень: підручник/ М. І. Пилипчук, А. С. Григор'єв, В. В. Шостак. - К.: Знання, 2007. - 270 с

КОНТРОЛЬНІ ПИТАННЯ ТА ЗАВДАННЯ

1. Загальна постановка задачі

2. Планування результатів експериментальних досліджень для отримання математичних моделей

3. Обробка результатів експериментальних досліджень для отримання математичних моделей

4. Алгебраїчні методи перетворення систем рівнянь для вирішення задач лінійного програмування

Лекція №13 Модуль 2. Розробка технічної документації щодо організації наукових досліджень

Тема 13: «Оформлення результатів експерименту. Закони розподілу випадкових величин.»

13.1Основні властивості кривої нормального розподілу

13.2Цільова функція, обмеження та граничні умови при побудові моделі (опису) об’єкта

12.3Перелік рекомендованої літератури

КОНТРОЛЬНІ ПИТАННЯ ТА ЗАВДАННЯ

МЕТА ЛЕКЦІЇ: Надати студентам знання про закони розподілу випадкових величин, основних властивостях кривої нормального закону розподілу

13. Оформлення результатів експерименту.

Закони розподілу випадкових велечин

13.1Основні властивості кривої нормального розподілу

Основні властивості кривої нормального розподілу:

− при всіх значеннях аргументу функція розподілу має додатнє значення;

− вісь абсцис є горизонтальною асимптотою кривої нормального розподілу;

− функція має максимум при , при цьому графік функції симетричний відносно прямої ;

− у межах поля розсіювання Δ = 6σ знаходяться 99,73 % всіх можливих значень у;

− площу під кривою приймають за 1 або 100 %.

Крива нормального розподілу залежить від статистичних показників вибірки. Для її побудови розраховують координати на осях абсцис та ординат за відповідними формулами:

, (13.1)

, (13.2)

де Z – координати в долях від σ, Z = 0 … 3 (крок 0,1 або 0,2); – табличне значення функції, яке залежить від Z; Δу – величина інтервалу: ; K – кількість інтервалів у вибірці (К = 1 + 3,2 lg N); N – обсяг вибірки (кількість вимірювань, спостережень).

Гіпотезу про нормальний розподіл перевіряють різними способами: застосуванням критеріїв асиметрії А, ексцесу Е і Пірсона χ².

Показники А і Е розраховують за формулами:

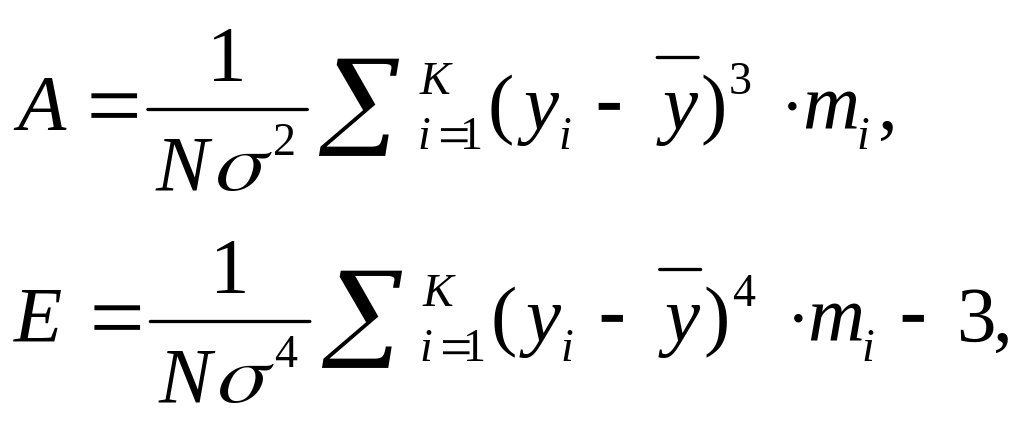(13.3)

де – кількість значень із вибірки обсягом N, які потрапили у відповідний інтервал.

Асиметрія характеризує несиметричність розподілу відносно середнього значення вибірки, ексцес – пологість розподілу (рис. 1.1).

а б

Рис. 1.1. Розподіл з різними значеннями асиметрії (а) та ексцесу (б)

Останньою процедурою в цих діях є розрахунок середньоквадратичних відхилень σ , σ :

; (13.4)

. (13.5)

Гіпотеза про нормальний розподіл вихідної величини приймається у випадку, коли відношення А/σ чи А/σ < 3.

Розрахункове значення критерію Пірсона визначають за формулою:

, (13.6)

де – ймовірність потрапляння випадкової величини у кожний інтервал.

Гіпотеза про нормальність розподілу вихідної величини приймається за умову виконання співвідношення: (табличне значення критерію Пірсона).

Приклад щодо застосування статистичного аналізу наведено в розд. 8.

Наступною процедурою є статистичний аналіз рівняння регресії (математичної моделі), який вирішує два основних завдання: оцінку значущості коефіцієнтів регресії і перевірку адекватності математичної моделі.

Оцінка значущості коефіцієнтів регресії (моделі) здійснюється, в першу чергу, з метою того, що обчислені за результатами експериментів коефіцієнти значною мірою є випадковими величинами.

Значущість коефіцієнтів визначають за критерієм Стьюдента:

, (13.7)

де r – коефіцієнт кореляції, який завжди знаходиться в межах -1 < r < +1; n – кількість дослідів.

Умова обумовлює існування статистичного зв`язку між параметрами.

Коефіцієнт регресії вважають статистично значущим при виконанні умови: , що і обумовлює необхідність включення його до математичної моделі (рівняння регресії).

Міра близькості поверхні відгуку до реальної поверхні визначається за допомогою критерію Фішера, тобто шляхом перевірки адекватності рівняння регресії. В основі цієї процедури лежить перевірка гіпотези, що характеризує розбіжність між результатами експерименту і величинами обчисленими за рівнянням регресії і виявляє спільність походження похибок. Ця процедура здійснюється так.

1. Визначають дисперсію адекватності:

, (13.8)

де n – кількість дубльованих дослідів; N – кількість дослідів; l – кількість значущих коефіцієнтів регресії; – відповідно експериментальне і розрахункове (аналітичне) значення функції відгуку в і-досліді.

2. Визначають дисперсію відтворюваності:

, (13.9)

де – дисперсія функції відгуку.

3. Визначають критерій Фішера:

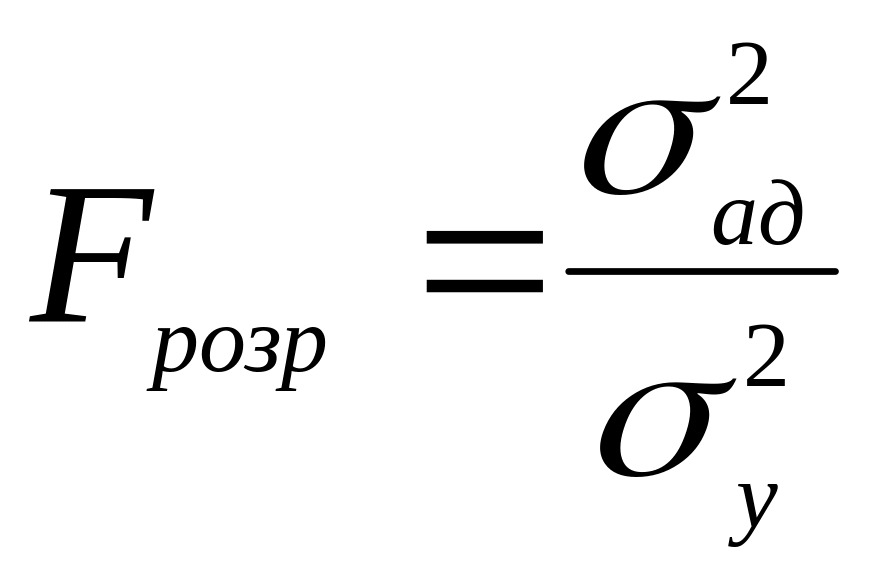(13.10)

4. Перевіряють гіпотезу про адекватність, яка повинна задовольняти таку умову:

. (13.11)