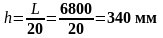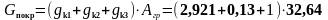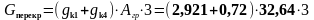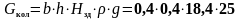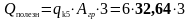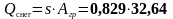- •1 Расчёт монолитного железобетонного перекрытия с балочными плитами
- •1.1 Проектирование компоновочной схемы
- •1.2 Предварительное назначение размеров поперечных сечений элементов перекрытия
- •1.3 Расчёт монолитной плиты
- •1.3.1 Определение нагрузок
- •1.3.2 Статический расчёт монолитной плиты
- •1.3.3 Расчет прочности нормальных сечений
- •1.3.4 Расчет прочности наклонных сечений
- •1.4 Расчёт второстепенной балки
- •1.4.1 Исходные данные
- •Определение нагрузок
- •1.4.2 Определение эффективных пролетов
- •1.4.3Определение расчетных усилий
- •1.4.4 Расчет прочности нормальных сечений
- •1.4.5 Построение эпюры материалов и определение мест обрыва арматуры второстепенной балки
- •1.4.6 Расчет поперечной арматуры
- •2 Расчет сборного многопролетного ригеля
- •2.1 Проектирование ригеля
- •2.2 Определение расчетных пролетов
- •2.4 Подсчет нагрузок
- •2.5 Определение нагрузки на ригель
- •2.6 Построение эпюр изгибающих моментов
- •А) эпюра изгибающих моментов без распределения усилий; б) – г) эпюры перераспределение усилий; д) эпюра изгибающих моментов с учётом перераспределения усилий; е) эпюра поперечных сил
- •2.7 Расчет прочности нормальных сечений
- •2.8 Построение эпюры материалов и определение мест обрыва арматуры ригеля
- •2.9 Расчет прочности наклонных сечений по поперечной силе
- •3 Расчет колонны первого этажа
- •3.1 Исходные данные
- •3.2 Подсчет нагрузок
- •3.3 Расчет колонны на прочность
- •3.3.1 Определение размеров сечения колонны
- •3.3.2 Расчёт продольного армирования колонны первого этажа
- •3.3.3 Расчет консоли колонны
- •3.3.4Армирование консоли
- •3.3.5 Конструирование стыка ригеля с колонной
- •3.3.6Конструирование стыка колонн
- •Список использованных источников
в крайнем пролёте и на крайней опоре:
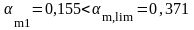
в среднем пролёте и на средней опоре:
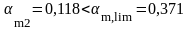
так как условие выполняется, то вычисляем площадь продольной арматуры:
в крайнем пролёте и на крайней опоре:
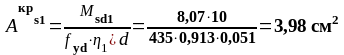
в среднем пролёте и на средней опоре:
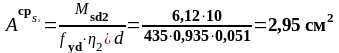
определяем минимальную площадь сечения арматуры определяем по ТКП EN 1992-1-1-2009 (стр.125, п 9.2.1.1) [6]
 (1.14)
(1.14)
где
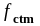 - средняя прочность
бетона на растяжение определяема по
ТКП EN
1992-1-1-2009 (стр.12, табл.3.1,
- средняя прочность
бетона на растяжение определяема по
ТКП EN
1992-1-1-2009 (стр.12, табл.3.1,
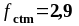 )
[6];
)
[6];
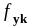 -
предел текучести стали определяем по
национальному приложению ТКП EN
1992-1-1-2009 (стр.197, 3.2.2(3)Р,
-
предел текучести стали определяем по
национальному приложению ТКП EN
1992-1-1-2009 (стр.197, 3.2.2(3)Р,
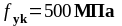 )
[6];
)
[6];
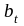 -
средняя ширина зоны растяжения (
-
средняя ширина зоны растяжения ( );
);
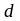 -
рабочая высота (
-
рабочая высота (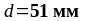 ).
).
Подставляя значения в формулу (1.14) получаем:
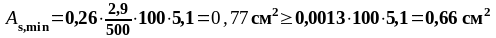
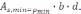
проверяем условие
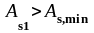
Условие выполняется
Таблица 1.2 - Требуемая площадь сечения арматуры на 1 м2 плиты
|
Msd, кНм |
m |
|
Площадь сечения, см2 |
|
As1 |
As, min |
||||
Крайний пролет и крайняя опора при непрерывном армировании |
8,07 |
0,155 |
0,913 |
3,98 |
0,77 |
Средние пролеты и средние опоры |
6,12 |
0,118 |
0,935 |
2,95 |
|
В соответствии с полученными значениями AS принимаем следующие сетки по методическим указаниям [1, табл. 7,8,9; ст. 12,14]:
-
в средних пролетах и на средних опорах
С1 (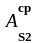 = 2,95 см2):
= 2,95 см2):
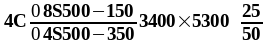
AS1 = 3,35 см2, сетка С1 имеет продольную рабочую арматуру, поперечную – распределительную.
- в первом пролете и на промежуточной опоре дополнительная сетка С2 (AS = 3,98 - 2,95 = 1,03 см2).
В соответствии с методическими указаниями [1, стр. 14], дополнительная сетка укладывается в крайних пролётах и на первых промежуточных опорах на 1/4 пролёта плиты.
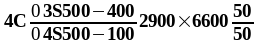
AS2 = 1,26 см2, сетка С2 имеет продольную распределительную арматуру, поперечную – рабочую.
- над главными балками устанавливаются верхние сетки конструктивно, площадь сечения поперечных стержней которых должна составлять не менее 1/3 пролетной арматуры плиты:
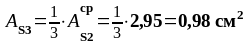
В соответствии с методическими указаниями [1, стр. 14], длину рабочих стержней назначают из условия, что расстояние от грани балки в каждую сторону было не менее 1/4 пролёта плиты:
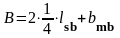 (1.15)
(1.15)
Подставив в (1.15) получаем:
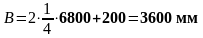
Над главными балками принимаем сетки С3:

AS3 = 0,98 см2, сетка С3 имеет продольную рабочую арматуру, поперечную – распределительную.
Схема армирования монолитной плиты в графической части лист 1.
1.3.4 Расчет прочности наклонных сечений
Расчет производится для сечения у первой промежуточной опоры слева, где действует наибольшая поперечная сила.
 кН
кН
Расчет
прочности железобетонных элементов на
действие поперечных сил начинается в
соответствии с п.6.2.1 (3) [6] проверкой
условия
 ,
где
,
где
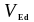 - расчётное значение поперечной силы в
сечении, возникающей от внешней нагрузки;
- расчётное значение поперечной силы в
сечении, возникающей от внешней нагрузки;
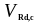 -
расчётное значение сопротивления
поперечной силе элемента без поперечной
арматуры определяемое по формуле (1.16)
в соответствии с п.6.2.2, (6.2a)
(1) [6].
-
расчётное значение сопротивления
поперечной силе элемента без поперечной
арматуры определяемое по формуле (1.16)
в соответствии с п.6.2.2, (6.2a)
(1) [6].
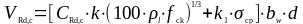 (1.16)
(1.16)
но не менее в соответствии с п 6.2.2, (6.2b) (1) [6]:
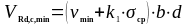 (1.17)
(1.17)
где fck= 30 МПа;
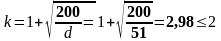
Принимаем
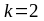 .
.
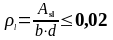 (1.18)
(1.18)
где Asl - площадь сечения растянутой арматуры, которая заведена не менее чем на lbd + d за рассматриваемое сечение (Asl = 3,35 см2);
bw – наименьшая ширина поперечного сечения в пределах растянутой зоны (b = 1000 мм).
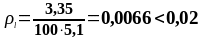
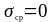 ,
при отсутствии осевого усилия (сжимающей
силы);
,
при отсутствии осевого усилия (сжимающей
силы);
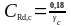 -
по национальному приложению таблица
НП.1, 6.6.4 (1) [6];
-
по национальному приложению таблица
НП.1, 6.6.4 (1) [6];
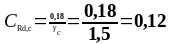
 -
по национальному приложению таблица
НП.1, 6.6.4 (1) [6];
-
по национальному приложению таблица
НП.1, 6.6.4 (1) [6];
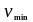 -
определяем по формуле (1.19) в
соответствии с п.6.2.2, (6.3N)
(1) [6] 5,47723
-
определяем по формуле (1.19) в
соответствии с п.6.2.2, (6.3N)
(1) [6] 5,47723
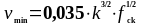 (1.19)
(1.19)
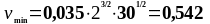
Подставим все значения в формулы (1.16) и (1.17):
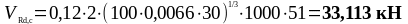
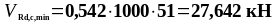
Так
как
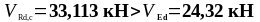 ,
то поперечная арматура не требуется.
,
то поперечная арматура не требуется.
1.4 Расчёт второстепенной балки
1.4.1 Исходные данные
Размеры второстепенной балки: lsb = 6800 м, bsb = 180 мм, hsb = 440 мм, шаг второстепенных балок Ssb = ls = 2400 мм. Размеры сечения главной балки bmb = 200 мм, hmb = 480 мм.
Определение нагрузок
Определим расчетную нагрузку (таблица 1.3) на один погонный метр второстепенной балки, собираемую с грузовой полосы шириной равной шагу второстепенных балок (ls = 2400 мм).
Таблица 1.3 – Нагрузка на один погонный метр второстепенной балки
Вид нагрузки |
Нормативная нагрузка, кН/м2 |
Коэфф. надежности по нагрузке (ТКП EN 1990-2011 [2], ст 59, таблица А.2(А), примечание 2) |
Расчетная нагрузка, кН/м2 |
1 |
2 |
3 |
4 |
Постоянные |
|||
Собственный вес плиты и конструкции пола: gk∙ ls = 2,72 ∙ 2,4
|
6,53 |
1,35 |
8,81 |
Собственный вес второстепенной балки: (hsb - hs)∙bsb ∙ =(0,44-0,08 )∙0,18∙25
|
1,62 |
1,35 |
2,19 |
Переменные |
|||
Производственные и промышленные складские помещения (qk = 6 кН/м2 в соответствии с национальным приложением ТКП EN 1991-1-1-2016 [5], ст.38, табл. НП6.4): qk ∙ ls = 6 ∙ 2,4 |
14,4 |
1,5 |
21,6 |
Найдём расчётную нагрузку на второстепенную балку через сочетание нагрузок по формуле (1.7):
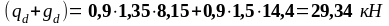
1.4.2 Определение эффективных пролетов
Эффективный пролёт определяют по формулам в соответствии с ТКП EN 1992-1-1-2009 (ст. 41, п 5.3.2.2) [6] (рисунок 1.5):
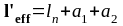 (1.16)
(1.16)
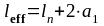 (1.17)
(1.17)
где - расстояние в свету между краями опор;
- min{1/2hsb; 1/2bmb};
- min{1/2hsb,sup; 1/2hsb}.
крайние:
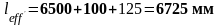 ;
;
средние:
 .
.
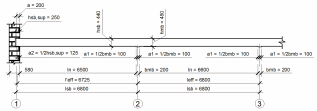
Рисунок 1.5 - К определению расчетных пролетов второстепенной балки
1.4.3Определение расчетных усилий
Ординаты огибающей эпюры изгибающих моментов вычисляются в сечениях через 0,2leff по формуле (1.18) в соответствии с методическими указаниями (стр. 7, (6)) [1]:
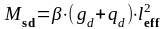 (1.18)
(1.18)
где
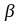 -
коэффициент для
определения ординат моментов эпюры в
соответствии с методическими указаниями
(рисунок 3, табл.6, стр.8) [1];
-
коэффициент для
определения ординат моментов эпюры в
соответствии с методическими указаниями
(рисунок 3, табл.6, стр.8) [1];
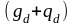 -
расчётная нагрузка
на второстепенную балку (п. 1.4.1) ;
-
расчётная нагрузка
на второстепенную балку (п. 1.4.1) ;
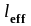 -
эффективный пролёт (п. 1.4.2).
-
эффективный пролёт (п. 1.4.2).
Значения коэффициентов для определения ординат отрицательных моментов принимаем по отношению:
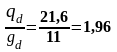
где
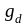 - постоянная
нагрузка (
- постоянная
нагрузка (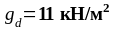 );
);
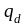 -
переменная нагрузка (
-
переменная нагрузка (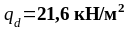 ).
).
Определение изгибающих моментов в различных сечениях второстепенной балки будем производить в табличной форме:
Таблица 1.4 - Определение расчетных значений изгибающих моментов
№ пролета |
№ точек |
В долях пролета |
|
|
Изгибающий момент– Мsd, кН м |
||
+ |
- |
+Мsd |
-Мsd |
||||
I |
1 |
0,2 l‘eff |
0,065 |
|
1326,920 |
86,250 |
|
2 |
0,4 l‘eff |
0,09 |
|
119,423 |
|
||
max |
0,425 l‘eff |
0,091 |
|
120,750 |
|
||
3 |
0,6 l‘eff |
0,075 |
|
99,519 |
|
||
4 |
0,8 l‘eff |
0,02 |
|
26,538 |
|
||
5 |
1,0 l‘eff |
|
-0,0715 |
|
-94,875 |
||
II |
6 |
0,2 leff |
0,018 |
-0,0297 |
1356,682 |
24,420 |
-40,293 |
7 |
0,4 leff |
0,058 |
-0,0085 |
78,688 |
-11,532 |
||
max |
0,5 leff |
0,0625 |
|
84,793 |
|
||
8 |
0,6 leff |
0,058 |
-0,0055 |
78,688 |
-7,462 |
||
9 |
0,8 leff |
0,018 |
-0,0237 |
24,420 |
-32,153 |
||
10 |
1,0 leff |
|
-0,0625 |
|
-84,793 |
||
III |
11 |
0,2 leff |
0,018 |
-0,0227 |
1356,682 |
24,420 |
-30,797 |
12 |
0,4 leff |
0,058 |
-0,0024 |
78,688 |
-3,256 |
||
max |
0,5 leff |
0,0625 |
|
84,793 |
|
||
Нулевые точки эпюры положительных моментов расположены на расстояниях 0,15 leff от грани опор:
- в крайнем пролёте: 0,15∙6,725 = 1,009 м
- в среднем пролёте: 0,15∙6,8 = 1,020 м
Положение нулевой точки отрицательных моментов в 1-м пролёте:
X0 = 0,2482∙l’eff = 0,2482∙6,725 = 1,669 м
Перерезывающие силы (у граней опор):
- у опоры А:
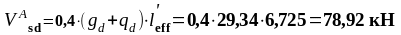
- у опоры В слева:
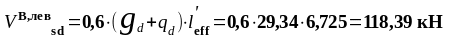
- у опоры В справа и у остальных опор:
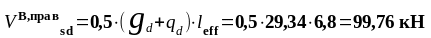
Строим эпюру усилий (рисунок 1.6).
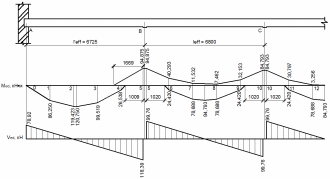
Рисунок 1.6 - Эпюра усилий во второстепенной балке
1.4.4 Расчет прочности нормальных сечений
Характеристики материалов:
Для бетона класса С30/37 :
нормативное сопротивление бетона по ТКП EN 1992-1-1-2009 (стр.12, табл.3.1) [6] - fck= 30 МПа;
расчетное сопротивление бетона при частном коэффициенте безопасности по бетону в соответствии с ТКП EN 1992-1-1-2009 (стр.18, п 3.1.6) [6]:
(1.19)
где - коэффициент, учитывающий влияние длительных эффектов на прочность бетона на растяжение и неблагоприятного способа приложения нагрузки в соответствии с национальным приложением ТКП EN 1992-1-1-2009 (стр.197, табл.НП.1, 3.1.6 (1)P) [6] ( );
- частный коэффициент безопасности для бетона по ТКП EN 1992-1-1-2009 (стр.9, табл.2.1N, ) [6].
Подставив в формулу (1.19) значения получаем:
значение предельной относительной деформации бетона при сжатии определяем по ТКП EN 1992-1-1-2009 (стр.12, табл.3.1) [6] -
По методическим указаниям [1, табл. П7] для бетона С30/37 : ,К2 = 0,416,
Расчетные характеристики арматуры класса S500:
расчётное сопротивление по методическим указаниям [1, табл. П3]: - fyd = 435 МПа;
модуль упругости по ТКП EN 1992-1-1-2009 (стр.24, п 3.2.7 (4)) [6] – Еs = 200 ГПа = 2·105 МПа
Определение требуемой площади сечения арматуры при действии положительного момента ведем как для таврового сечения с полкой в сжатой зоне. При действии отрицательного момента полка находится в растянутой зоне, следовательно, расчетное сечение будет прямоугольным.
Определим эффективную ширину полки тавра по ТКП EN 1992-1-1-2009 (стр.40, п 5.3.2.1) [6]. Эффективную ширину плиты, как правило, необходимо определять на основании расстояния l0 между точками нулевых моментов (рисунок 1.7), где l’eff = 6725 мм и leff =6800 мм (стр. 7, п 1.3.2).
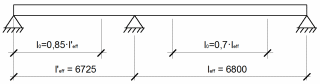
Рисунок 1.7 – Определение l0 для расчёта эффективной ширины полки
Определим l0 :


Определим параметры эффективной ширины полки (рисунок 1.8), где bw = bsb = 180 мм ; b1 = 3362,5 мм; b2 = 3400 мм; b = ls = 2400 мм.

Рисунок 1.8 – Параметры эффективной ширины полки
Эффективная ширина полки beff для тавровых балок выводится из уравнения:
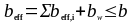 (1.20)
(1.20)
При этом
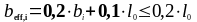 (1.21)
(1.21)
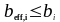 (1.22)
(1.22)
Подставляя значения в формулу (1.21) получаем:

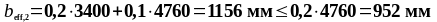
Условие не выполняется, следовательно принимаем:
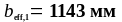
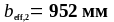
Проверим условие (1.22):
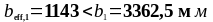
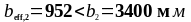
Условие выполняется.
Определим эффективную ширину полки по формуле (1.20):

Условие выполняется.
Принятое расчётное сечение в пролёте рисунок 1.9
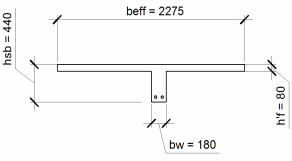
Рисунок 1.9 – Сечение балки в пролёте принятое к расчёту
Принятое расчётное сечение на опорах будет иметь вид (рисунок 1.10):
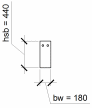
Рисунок 1.10 – Сечение балки на опорах принятое к расчёту
Размеры сечения, принятые для расчета:
beff = 2275 мм; hsb = 440 мм; bsb = 180 мм; hf’ = 80 мм;
Рабочую
высоту сечения для таврового сечения
и прямоугольного будем определять
исходя из конструктивного размещения
арматуры, минимального диаметра арматуры
( =12
мм) и вертикального расстояния в свету
между параллельными стержнями, которое
в соответствии с ТКП EN
1992-1-1-2009 (стр.107, п 8.2 (2)) [6] должно быть не
менее чем максимальное значение из
следующих: k1
– диаметр стержня, или (dg+k2)
= 5+20 = 25 мм (где dg
– диаметр наибольшего зерна заполнителя
(dg
= 20 мм
(щебень)), или 20 мм. Значения k1
и k2
соответственно
приведены в национальном приложении
(стр.201, п 8.2 (2)) [6] (применяются значения
k1
= 1 мм и k2
= 5 мм). Следовательно расстояние в свету
между стержнями будет составлять 25 мм.
=12
мм) и вертикального расстояния в свету
между параллельными стержнями, которое
в соответствии с ТКП EN
1992-1-1-2009 (стр.107, п 8.2 (2)) [6] должно быть не
менее чем максимальное значение из
следующих: k1
– диаметр стержня, или (dg+k2)
= 5+20 = 25 мм (где dg
– диаметр наибольшего зерна заполнителя
(dg
= 20 мм
(щебень)), или 20 мм. Значения k1
и k2
соответственно
приведены в национальном приложении
(стр.201, п 8.2 (2)) [6] (применяются значения
k1
= 1 мм и k2
= 5 мм). Следовательно расстояние в свету
между стержнями будет составлять 25 мм.
Определим рабочую высоту прямоугольного сечения (рисунок 1.11):
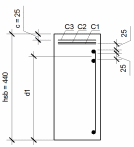
Рисунок 1.11 – К определению рабочей высоты
Исходя из рисунка 1.11 рабочая высота d1 будет определяться как:
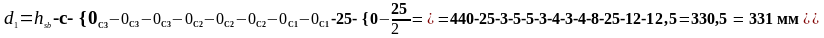
Определим рабочую высоту таврового сечения (рисунок 1.12):
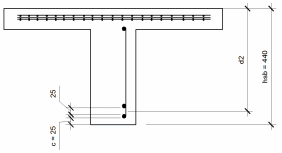
Рисунок 1.12 – К определению рабочей высоты
Исходя из рисунка 1.12 рабочая высота d2 будет определяться как:
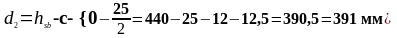
Расчет проводится по упрощенному деформационному методу в соответствии с методическими указаниями [1,стр. 16-17]. Предполагая, что нейтральная ось проходит по нижней грани полки, определяем область деформирования для прямоугольного сечения beff = 2275 мм и положение нейтральной оси при расчете тавровых сечений:
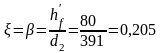
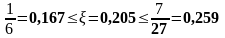
Определяем величину изгибающего момента, воспринимаемую бетоном сечения, расположенного в пределах высоты полки:
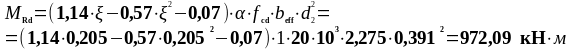
Так
как
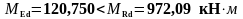 ,
то нейтральная ось расположена в пределах
полки. Сечение рассматривается как
прямоугольное с
,
то нейтральная ось расположена в пределах
полки. Сечение рассматривается как
прямоугольное с
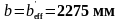 .
.
Для
арматуры S500
(стр.11):
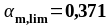
В пролете 1. (нижняя арматура): MEd = 120,750 кН∙м, d2 = 391 мм, b = beff = 2275 мм.
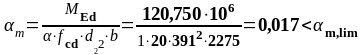
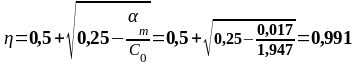
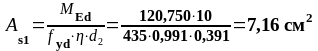
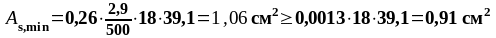
В пролете 2. (нижняя арматура): MEd = 84,793 кН∙м, d2 = 391 мм, b= beff = 2275 мм

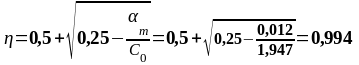
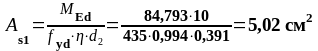
В опорных сечениях действуют отрицательные моменты, плита расположена в растянутой зоне, поэтому сечения балки рассматриваются как прямоугольные шириной b = 180 мм.
На опоре В. (верхняя арматура): MEd = 94,875 кН∙м, d1 = 331 мм, b = bsb= 180 мм
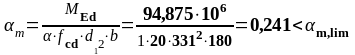
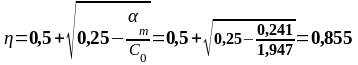
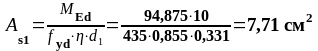
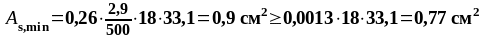
В
пролете 2. (верхняя
арматура): MEd
=
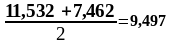 кН∙м,
d1
= 331 мм,
b
= bsb=
180 мм
кН∙м,
d1
= 331 мм,
b
= bsb=
180 мм

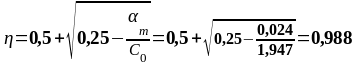
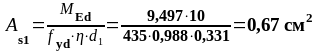
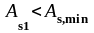
Следовательно
принимаем
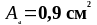 .
.
На опоре С. (верхняя арматура): MEd = 84,793 кН∙м, d1 = 331 мм, b = bsb= 180 мм
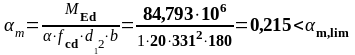
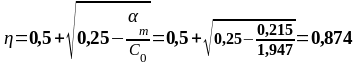
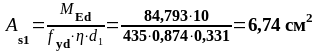
Результаты расчетов и подбор арматуры в расчетных сечениях сводим в таблицу 1.5.
Таблица 1.5 - Определение площади сечения рабочей арматуры второстепенной балки
Положение сечения |
Расположение арматуры |
М, kН м |
|
|
см2 |
см2 |
Принятое армирование |
||
1 пролет |
Нижняя |
120,750 |
0,017 |
0,991 |
7,16 |
7,35 |
2 2 18 |
||
1 пролет |
Верхняя |
– |
Монтажная конструктивная арматура |
3,08 |
2 14 |
||||
Опора В |
Верхняя |
-94,875 |
0,241 |
0,855 |
7,71 |
8,17 |
2 14 2 18 |
||
2 пролет |
Нижняя |
84,793 |
0,012 |
0,994 |
5,02 |
5,34 |
2 12 2 14 |
||
2 пролет |
Верхняя |
-9,497 |
0,024 |
0,988 |
0,9 |
2,26 |
2 12 |
||
Опора С |
Верхняя |
-84,793 |
0,215 |
0,874 |
6,74 |
7,35 |
2 12 2 18 |
||
1.4.5 Построение эпюры материалов и определение мест обрыва арматуры второстепенной балки
На огибающей эпюре MEd построим эпюру MRd, которая характеризует несущую сечений балки по арматуре. Несущая способность сечений балки по арматуре определяется по формуле:
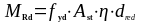 (1.23)
(1.23)
где
 - уточненное значение рабочей высоты
сечения, определяемое по формуле:
- уточненное значение рабочей высоты
сечения, определяемое по формуле:
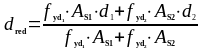 (1.24)
(1.24)
где
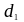 и
и
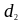 - расстояние до центра арматуры.
- расстояние до центра арматуры.
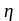 -
табличный коэффициент, определяемый:
-
табличный коэффициент, определяемый:
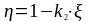 (1.25)
(1.25)
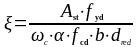 (1.26)
(1.26)
Подбор нижней продольной арматуры в первом пролете:
As1 = 2,26 см2, As2 = 5,09 см2 ,b = beff = 2275 мм, , К2 = 0,416, fyd = 435 МПа, fсd = 20 МПа.

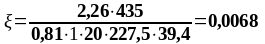
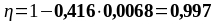
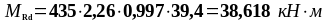
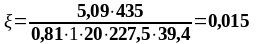
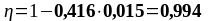

Подбор нижней продольной арматуры во втором пролете:
As1 = 2,26 см2, As2 = 3,08 см2 ,b = beff = 2275 мм, , К2 = 0,416, fyd = 435 МПа, fсd = 20 МПа.
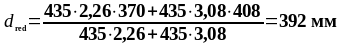
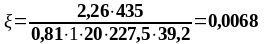
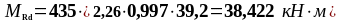
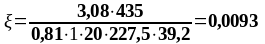
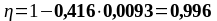
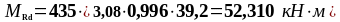
Подбор верхней продольной арматуры на опоре В:
As1 = 3,08 см2, As2 = 3,08 см2,b = bsb = 180 мм, , К2 = 0,416, fyd = 435 МПа, fсd = 20 МПа.
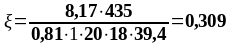
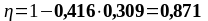
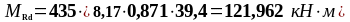
Подбор верхней продольной арматуры на опоре C:
As1 = 5,09 см2, As2 = 2,26 см2,b = bsb = 180 мм, , К2 = 0,416, fyd = 435 МПа, fсd = 20 МПа.
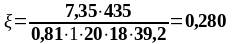
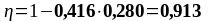
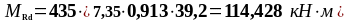
Подбор верхней продольной арматуры в первом и втором пролете:
As1 = 3,08 см2 и As1 = 2,26 см2, b = bsb = 180 мм, , К2 = 0,416, fyd = 435 МПа, fсd = 20 МПа.
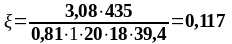
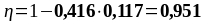
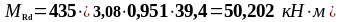
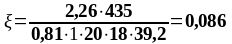
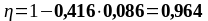
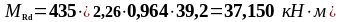
Расчеты, необходимые для построения эпюры материалов сведены в таблицу 1.6.
Анкеровку продольной арматуры определяем в соответствии с [6] (стр.109-112, п.8.4):
Расчетное значение предельного напряжения сцепления fbd для стержней периодического профиля может быть рассчитано следующим образом:
 (1.27)
(1.27)
где
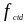 - расчетное значение
предела прочности бетона при растяжении
согласно (3.1.6 (2)Р,) [6];
- расчетное значение
предела прочности бетона при растяжении
согласно (3.1.6 (2)Р,) [6];
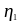 -
коэффициент, учитывающий качество
сцепления и положение стержней во время
бетонирования (рисунок 8.2, стр.110) (
-
коэффициент, учитывающий качество
сцепления и положение стержней во время
бетонирования (рисунок 8.2, стр.110) (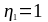 - для хороших условий;
- для хороших условий;
 - для всех других случаев) [6];
- для всех других случаев) [6];
 -
для
-
для
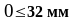 ;
;
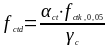 (1.28)
(1.28)
где
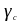 - частный коэффициент
безопасности для бетона (
- частный коэффициент
безопасности для бетона (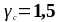 )
(стр.9 табл.2.1N)
[6];
)
(стр.9 табл.2.1N)
[6];
 -
коэффициент, учитывающий влияние
длительных эффектов на прочность бетона
на растяжение и неблагоприятного способа
приложения нагрузки (стр.197, 3.1.6 (2)P) (
-
коэффициент, учитывающий влияние
длительных эффектов на прочность бетона
на растяжение и неблагоприятного способа
приложения нагрузки (стр.197, 3.1.6 (2)P) (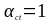 )
[6];
)
[6];
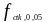 -
характеристическое значение предела
прочности бетона при осевом растяжении
(стр.12, табл.3.1) (
-
характеристическое значение предела
прочности бетона при осевом растяжении
(стр.12, табл.3.1) ( )
[6];
)
[6];
Требуемую базовую длину анкеровки lb,rqd для анкеровки усилия Asϭsd в прямом стержне при постоянном сцеплении fbd определяют по формуле:
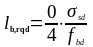 (1.29)
(1.29)
где
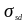 - расчетное
напряжение стержня в месте, от которого
измеряется анкеровка (
- расчетное
напряжение стержня в месте, от которого
измеряется анкеровка (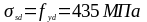 );
);
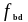 -
определяют по формуле (1.27);
-
определяют по формуле (1.27);
Расчётная длина анкеровки для сжатых стержней lbd составляет:
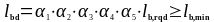 (1.30)
(1.30)
где
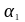 - коэффициент,
учитывающий влияние формы стержней при
достаточном защитном слое (стр.112,
табл.8.2) [6];
- коэффициент,
учитывающий влияние формы стержней при
достаточном защитном слое (стр.112,
табл.8.2) [6];
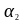 -
коэффициент, учитывающий влияние
минимальной толщины защитного слоя
бетона (стр.112, табл.8.2) [6];
-
коэффициент, учитывающий влияние
минимальной толщины защитного слоя
бетона (стр.112, табл.8.2) [6];
 -
коэффициент, учитывающий влияние
усиления поперечной арматурой (стр.112,
табл.8.2) [6];
-
коэффициент, учитывающий влияние
усиления поперечной арматурой (стр.112,
табл.8.2) [6];
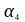 -
коэффициент, учитывающий влияние одного
или нескольких приваренных поперечных
стержней вдоль расчетной длины анкеровки
(стр.112, табл.8.2) [6];
-
коэффициент, учитывающий влияние одного
или нескольких приваренных поперечных
стержней вдоль расчетной длины анкеровки
(стр.112, табл.8.2) [6];
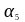 -
коэффициент, учитывающий влияние
поперечного давления плоскости
раскалывания вдоль расчетной длины
анкеровки (стр.112, табл.8.2) [6];
-
коэффициент, учитывающий влияние
поперечного давления плоскости
раскалывания вдоль расчетной длины
анкеровки (стр.112, табл.8.2) [6];
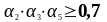 (1.31)
(1.31)
 -
определяют по формуле (1.29);
-
определяют по формуле (1.29);
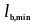 -
минимальная длина анкеровки, если не
действует другое ограничение принимают:
-
минимальная длина анкеровки, если не
действует другое ограничение принимают:
- для анкеровки при растяжении
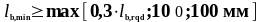 (1.32)
(1.32)
- для анкеровки при сжатии
 (1.33)
(1.33)
Расчётная длина анкеровки в соответствии с [6] (п.8.4.4 (2) стр.111) для растянутых стержней lb,eq составляет:
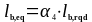 (1.34)
(1.34)
Определим по формуле (1.28) расчетное значение предела прочности бетона при растяжении:
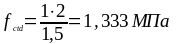
Анкеровка сжатой арматуры
Опора В:
В сечении обрываются стержни Ø18 мм класса S500.
Определим расчетное значение предельного напряжения сцепления по формуле (1.27):

Определим требуемую базовую длину анкеровки по формуле (1.29):
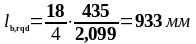
Определим минимальную длину анкеровки по формуле (1.33):
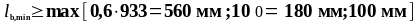
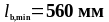
Определим расчётную длину анкеровки по формуле (1.30):
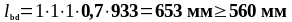
Принимаем
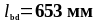 .
.
Опора С:
В сечении обрываются стержни Ø18 мм класса S500.
Определим расчетное значение предельного напряжения сцепления по формуле (1.27):
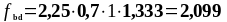
Определим требуемую базовую длину анкеровки по формуле (1.29):

Определим минимальную длину анкеровки по формуле (1.33):
Определим расчётную длину анкеровки по формуле (1.30):
Принимаем .
Анкеровка растянутой арматуры
1-ый пролёт нижняя арматура:
В сечении обрываются стержни Ø12 мм класса S500.
Определим расчетное значение предельного напряжения сцепления по формуле (1.27):
Определим требуемую базовую длину анкеровки по формуле (1.29):
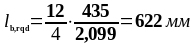
Определим эквивалентную длину анкеровки по формуле (1.34):
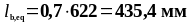
Принимаем
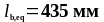 .
.
2-ой пролёт нижняя арматура:
В сечении обрываются стержни Ø12 мм класса S500.
Определим расчетное значение предельного напряжения сцепления по формуле (1.27):
Определим требуемую базовую длину анкеровки по формуле (1.29):
Определим эквивалентную длину анкеровки по формуле (1.34):
Принимаем .
Анкеровка арматуры на свободной опоре.
Длинна анкеровки продольной арматуры Ø12 мм на свободной опоре (в зоне опирания второстепенной балки на наружную стену) должна быть не менее 5·Ø = 5·12 = 60 мм. При площадке опирания второстепенной балки на стену lsb,sup = 250 мм анкеровка продольной арматуры обеспечивается.
Эпюра материалов представлена на рисунке 1.13.
Таблица 1.6 - Вычисление ординат эпюры материалов для продольной арматуры
и количество стержней |
dred, см |
As, см2 |
fyd, МПа |
|
|
|
1-й пролет (нижняя арматура, b = 2275 мм) |
||||||
2 12 2 18 2 12; 2 18 |
39,4 |
2,26 5,09 7,35 |
435 |
0,0068 0,015
|
0,997 0,994
|
38,618 86,714 125,332 |
1-й пролет (верхняя арматура, b = 180 мм) |
||||||
2 14 |
39,4 |
3,08 |
435 |
0,117 |
0,951 |
50,202 |
2-й пролет (нижняя арматура, b = 2275 мм) |
||||||
2 12 2 14 2 12; 2 14 |
39,2 |
2,26 3,08 5,34 |
435 |
0,0068 0,0093
|
0,997 0,996
|
38,422 52,310 90,732 |
2-й пролет (верхняя арматура, b = 180 мм) |
||||||
2 12 |
39,2 |
2,26 |
435 |
0,086 |
0,964 |
37,150 |
Опорная арматура (опора B, b = 180 мм) |
||||||
2 14 2 18 2 14; 2 18 |
39,4 |
8,17 |
435 |
0,309
|
0,871
|
121,962 |
Опорная арматура (опора С, b = 180 мм) |
||||||
2 12 2 18 2 12; 2 18 |
39,2 |
7,35 |
435 |
0,280 |
0,913 |
114,428 |
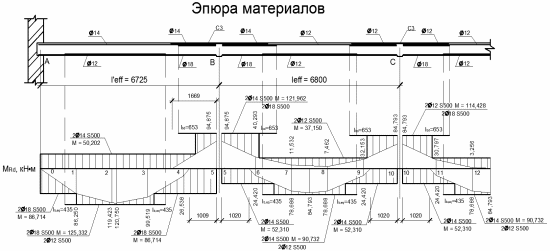
Рисунок 1.13 – Эпюра материалов
1.4.6 Расчет поперечной арматуры
Расчет производится для сечения у первой промежуточной опоры слева, где действует наибольшая поперечная сила.
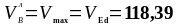 кНм
кНм
Расчет прочности железобетонных элементов на действие поперечных сил начинается в соответствии с п.6.2.1 (3) [6] проверкой условия , где - расчётное значение поперечной силы в сечении, возникающей от внешней нагрузки; - расчётное значение сопротивления поперечной силе элемента без поперечной арматуры определяемое по формуле (1.35) в соответствии с п.6.2.2, (6.2a) (1) [6].
(1.35)
но не менее в соответствии с п 6.2.2, (6.2b) (1) [6]:
 (1.36)
(1.36)
где fck= 30 МПа;
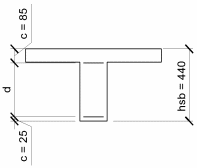
Рисунок 1.14 - К определению рабочей высоты
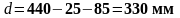

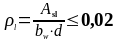 (1.37)
(1.37)
где Asl - площадь сечения растянутой арматуры, которая заведена не менее чем на lbd + d за рассматриваемое сечение (Asl = 7,35 см2);
bw – наименьшая ширина поперечного сечения в пределах растянутой зоны (bw = 180 мм).
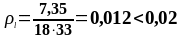
, при отсутствии осевого усилия (сжимающей силы);
- по национальному приложению таблица НП.1, 6.6.4 (1) [6];
- по национальному приложению таблица НП.1, 6.6.4 (1) [6];
- определяем по формуле (1.38) в соответствии с п.6.2.2, (6.3N) (1) [6]
(1.38)
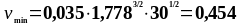
Подставим все значения в формулы (1.35) и (1.36):
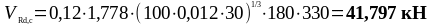
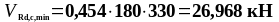
Так
как
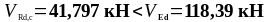 ,
необходим расчёт поперечной арматуры.
,
необходим расчёт поперечной арматуры.
Длина участка, на котором поперечное армирование необходимо устанавливать по расчёту, определяется по эпюре поперечных сил (рисунок 1.15).
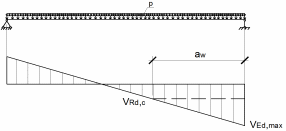
Рисунок 1.15 – К расчёту наклонных сечений
Определим расчётный участок:
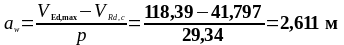
Согласно
п.6.2.3 (5) [6] в зонах без скачков и разрывов
на эпюре поперечной силы VEd
(например, при равномерно распределенной,
приложенной по верхней грани элемента
нагрузке) площадь поперечной арматуры
на любом отрезке длины
 может быть рассчитана по наименьшему
значению VEd
в данном отрезке.
может быть рассчитана по наименьшему
значению VEd
в данном отрезке.
Первое расчётное сечение назначим на расстоянии от опоры z1 = d = 330 мм.
Поперечное усилие в данном сечении:

Задаёмся
углом наклона к горизонтали
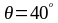 .
.
В пределах длины расчётного участка поперечное армирование рассчитывают из условий:
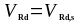 (1.39)
(1.39)
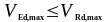 (1.40)
(1.40)
где
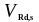 - расчетное значение поперечной силы,
которая может быть воспринята поперечной
арматурой, достигшей текучести, определяем
по формуле (1.41) в соответствии с п.6.2.3,
(6.8) (3) [6];
- расчетное значение поперечной силы,
которая может быть воспринята поперечной
арматурой, достигшей текучести, определяем
по формуле (1.41) в соответствии с п.6.2.3,
(6.8) (3) [6];
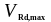 -
расчетное значение максимальной
поперечной силы, которая может быть
воспринята элементом, из условия
раздавливания сжатых подкосов определяем
по формуле (1.42) в соответствии с п.6.2.3,
(6.9) (3) [6].
-
расчетное значение максимальной
поперечной силы, которая может быть
воспринята элементом, из условия
раздавливания сжатых подкосов определяем
по формуле (1.42) в соответствии с п.6.2.3,
(6.9) (3) [6].
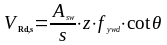 (1.41)
(1.41)
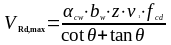 (1.42)
(1.42)
где
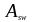 - площадь сечения поперечной арматуры
определяемая по формуле (1.43):
- площадь сечения поперечной арматуры
определяемая по формуле (1.43):
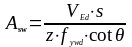 (1.43)
(1.43)
s – расстояние между хомутами;
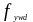 -
расчётное значение предела текучести
поперечной арматуры в соответствии с
примечанием п.6.2.3, (3) [6] :
-
расчётное значение предела текучести
поперечной арматуры в соответствии с
примечанием п.6.2.3, (3) [6] :
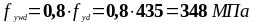
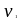 -
коэффициент понижения прочности бетона,
учитывающий влияние наклонных трещин
в соответствии с примечанием 1 п.6.2.3, (3)
[6]:
-
коэффициент понижения прочности бетона,
учитывающий влияние наклонных трещин
в соответствии с примечанием 1 п.6.2.3, (3)
[6]:
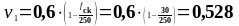
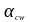 -
коэффициент, учитывающий уровень
напряжения в сжатом поясе в соответствии
с примечанием 3 п.6.2.3, (3) [6] (
-
коэффициент, учитывающий уровень
напряжения в сжатом поясе в соответствии
с примечанием 3 п.6.2.3, (3) [6] (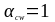 ).
).
Плечо внутренней пары сил в соответствии с п.6.2.3 (1) [6]:
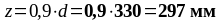
Принимаем шаг хомутов s = 100 мм.
Определим площадь поперечной арматуры по формуле 1.43:
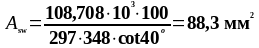
Принимаем по таблице П6 [1] 2ø8 (Asw = 101 мм2).
Максимальная площадь эффективной поперечной арматуры следует из условия п.6.2.3, (6.12) (3) [6]:
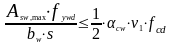 (1.44)
(1.44)
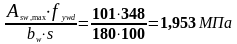
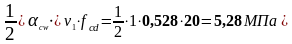
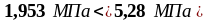
Определим поперечную силу, которая может быть воспринята полосой бетона между наклонными трещинами по формуле (1.42):
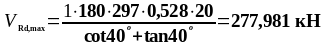
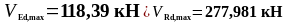
Расстояние от опоры до второго расчётного сечения:
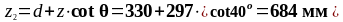
Действующее значение поперечной силы:
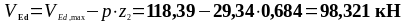
Требуемый шаг поперечной арматуры:
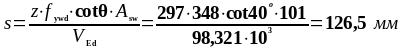
Максимальный шаг поперечной арматуры:
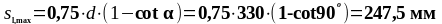
Расстояние от опоры до третьего расчётного сечения:
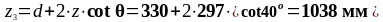
Действующее значение поперечной силы:
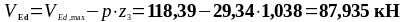
Требуемый шаг поперечной арматуры:
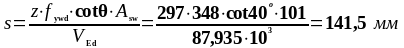
Расстояние от опоры до четвёртого расчётного сечения:
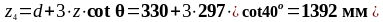
Действующее значение поперечной силы:
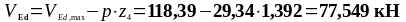
Требуемый шаг поперечной арматуры:
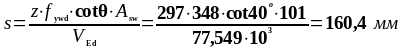
Расстояние от опоры до пятого расчётного сечения:
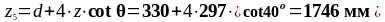
Действующее значение поперечной силы:

Требуемый шаг поперечной арматуры:
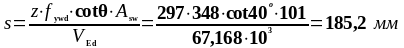
Расстояние от опоры до шестого расчётного сечения:

Действующее значение поперечной силы:
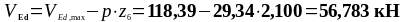
Требуемый шаг поперечной арматуры:
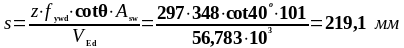
Расстояние от опоры до седьмого расчётного сечения:
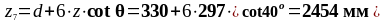
Действующее значение поперечной силы:

Требуемый шаг поперечной арматуры:
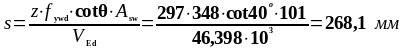
Расстояние от опоры до восьмого расчётного сечения:
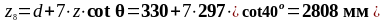
Действующее значение поперечной силы:
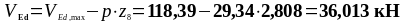
Требуемый шаг поперечной арматуры:

Результаты расчётов сведены в таблицу 1.7
Таблица 1.7 – Шаг стержней поперечной арматуры
Расстояние от опоры до расчётного сечения |
Наименьшее значение поперечной силы в сечении VEd, кН |
Шаг поперечных стержней по расчёту s, мм |
Допустимый шаг, мм |
||||
zi |
мм |
||||||
d |
330 |
108,708 |
114,4 |
100 |
|||
d+z∙cotθ |
684 |
98,321 |
126,5 |
||||
d+2∙z∙cotθ |
1038 |
87,935 |
141,5 |
||||
d+3∙z∙cotθ |
1392 |
77,549 |
160,4 |
||||
d+4∙z∙cotθ |
1746 |
67,168 |
185,2 |
||||
d+5∙z∙cotθ |
2100 |
56,783 |
219,1 |
200 |
|||
d+6∙z∙cotθ |
2454 |
46,398 |
268,1 |
||||
d+7∙z∙cotθ |
2808 |
36,013 |
345,4 |
||||
Таким образом на участке от грани опоры до сечения на расстоянии 2,1 м принят шаг хомутов s1 = 100 мм, а в середине пролёта s2 = 200 мм.
2 Расчет сборного многопролетного ригеля
2.1 Проектирование ригеля
Ориентировочные размеры поперечного сечения ригелей прямоугольной формы могут назначаться следующими:
- высота:
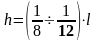 (2.1)
(2.1)
где l – пролет ригеля;
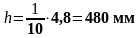
Принимаем h = 500 мм.
- ширина:
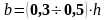 (2.2)
(2.2)
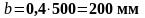
Принимаем b = 200 мм.
Компоновочная схема представлена на рисунке 2.1.
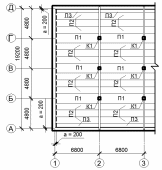
Рисунок 2.1 - Компоновка сборного ребристого перекрытия
2.2 Определение расчетных пролетов
Эффективный пролёт определяют по формулам (1.16) и (1.17) в соответствии с п.1.4.2, стр. 15. (рисунок 2.2):
(2.3)
(2.4)
где - расстояние в свету между краями опор;
- min{1/2h; 1/2b};
- min{1/2hsb,sup; 1/2hsb}.
крайние:
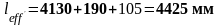 ;
;
средние:
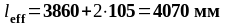 .
.
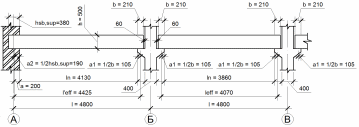
Рисунок 2.2 - К определению расчетных пролетов ригеля
2.4 Подсчет нагрузок
Нагрузку на 1 м2 поверхности плиты в кН/м2 приведена в таблице 2.1.
Таблица 2.1 - Нагрузки на 1м2 сборного перекрытия
Вид нагрузки |
Нормативная нагрузка, кН/м2 |
Коэффициент надежности по нагрузке |
Расчетная нагрузка, кН/м2 |
Постоянные |
|||
Бетонный пол ( = 0,04м, = 18 кН/м3) |
0,72 |
1,35 |
0,97 |
-
от собственного веса плиты при
Принимаем 350 мм |
2,4 |
1,35 |
3,24 |
Переменная |
|||
Производственные и промышленные складские помещения (функциональная) |
6 |
1,5 |
9 |
2.5 Определение нагрузки на ригель
Определим расчётные нагрузки на ригель с грузовой ширины 6800 мм, через сочетание нагрузок [2] (ст. 59, таблица А.2(А), примечание 2) при ширине грузовой площади 6,8 м и коэффициента воздействий kfi = 0,9 составят:
- постоянная:
gd = (0,97 + 3,24)∙ 6,8∙0,9 = 25,77 кH/м
- суммарная (с учетом нагрузки от ригеля) постоянная нагрузка:
g = 25,77 + (0,2 ∙ 0,5 ∙ 25 ∙ 6,8 ∙ 1,35∙0,9) = 46,43 кH/м
25 кН/м3 – удельный вес железобетона.
- переменная:
qd = 9∙6,8∙0,9 = 55,08 кH/м
Суммарная нагрузка будет равна:
(g+q)d = 46,43 + 55,08 = 101,51 кH/м
2.6 Построение эпюр изгибающих моментов
Ригель рассчитывается, как неразрезная 4-ех пролетная балка с шарнирным опиранием на колоны, с учетом перераспределения усилий.
Значения M и V на опорах определяем в программе «Эспри 2.1».
Варианты схем загружения представлены на рисунке 2.3.
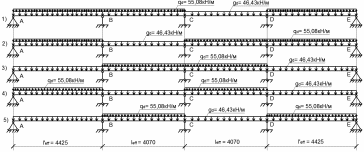
Рисунок 2.3 - Варианты загружения ригеля
Эпюры изгибающих моментов от загружений представлены на рисунке 2.4.
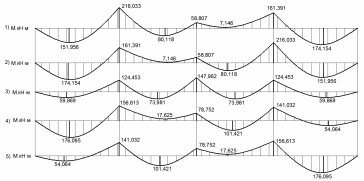
Рисунок 2.4 - Эпюры изгибающих моментов
Результаты расчётов сводим в таблицу 2.2.
Таблица 2.2 - Изгибающие моменты в ригеле
Вариант загруже-ния |
Сечения |
||||||
1-й пролёт |
Опора В |
2-й пролёт |
Опора С |
3-й пролёт |
Опора D |
4-й пролёт |
|
1 |
151,956 |
-216,033 |
80,118 |
-58,807 |
-7,146 |
-161,391 |
147,154 |
2 |
174,154 |
-161,391 |
-7,146 |
-58,807 |
80,118 |
-216,033 |
151,956 |
3 |
59,869 |
-124,453 |
73,981 |
-147,962 |
73,981 |
-124,453 |
59,869 |
4 |
176,095 |
-156,613 |
-17,625 |
-78,752 |
101,421 |
-141,032 |
54,064 |
5 |
54,064 |
-141,032 |
101,421 |
-78,752 |
-17,625 |
-156,613 |
176,095 |
Мmax |
176,095 |
-216,033 |
-17,625 |
-147,962 |
-17,625 |
-216,033 |
176,095 |
101,421 |
101,421 |
||||||
Затем строим эпюру изгибающих моментов, строим эпюры перераспределения усилий (13%) и строим эпюру изгибающих моментов с учётом перераспределения усилий (рисунок 2.5).
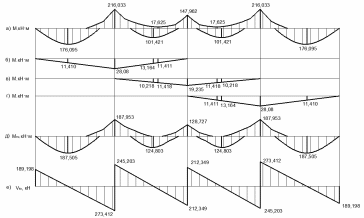
А) эпюра изгибающих моментов без распределения усилий; б) – г) эпюры перераспределение усилий; д) эпюра изгибающих моментов с учётом перераспределения усилий; е) эпюра поперечных сил
Рисунок 2.5 - Эпюра усилий в ригеле
2.7 Расчет прочности нормальных сечений
Характеристики материалов приведены в пункте 1.4.4 стр. 17.
Расчёт выполняем по алгоритму №1 методических указаний [1, стр. 9] упрощённым деформационным методом:
В пролете 1 (нижняя арматура): Med = 187,505 кН∙м
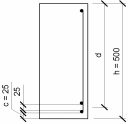
Рисунок 2.6 - К определению рабочей высоты сечения
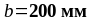

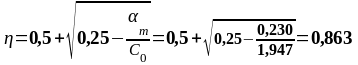
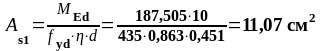
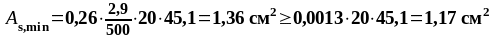
В пролете 2 (нижняя арматура): Med = 124,803 кН∙м
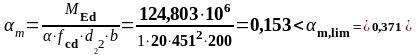

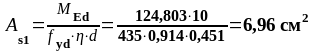
На опоре В (верхняя арматура): MEd = 187,953 кН∙м
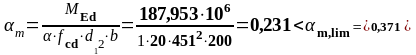
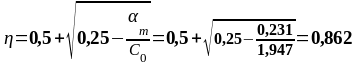
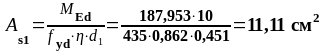
На опоре C (верхняя арматура): MEd = 128,727 кН∙м
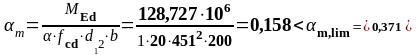
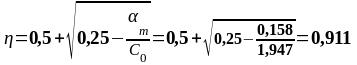
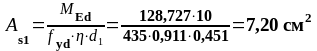
Результаты расчетов и подбор арматуры в расчетных сечениях сводим в таблицу 2.3.
Таблица 2.3 - Определение площади сечения рабочей арматуры ригеля
Положение сечения |
Расположение арматуры |
М, kН м |
|
|
, см2 |
, см2 |
Принятое армирование |
||
1 пролет |
Нижняя |
187,505 |
0,230 |
0,863 |
11,07 |
11,62 |
2 16 2 22 |
||
1 пролет |
Верхняя |
- |
Монтажная конструктивная арматура |
4,02 |
2 16 |
||||
Опора В |
Верхняя |
-187,953 |
0,231 |
0,862 |
11,11 |
11,62 |
2 16 2 22 |
||
2 пролет |
Нижняя |
124,803 |
0,153 |
0,914 |
6,96 |
7,1 |
2 14 2 16 |
||
2 пролет |
Верхняя |
- |
Монтажная конструктивная арматура |
4,02 |
2 16 |
||||
Опора С |
Верхняя |
-128,727 |
0,158 |
0,911 |
7,20 |
8,04 |
2 16 2 16 |
||
2.8 Построение эпюры материалов и определение мест обрыва арматуры ригеля
На огибающей эпюре MEd построим эпюру MRd, которая характеризует несущую сечений балки по арматуре. Расчёт выполняем в соответствии с пунктом 1.4.5, стр. 25.
Подбор нижней продольной арматуры в первом пролете:
As2 = 4,02 см2, As1 = 7,6 см2 ,b = 200 мм, , К2 = 0,416, fyd = 435 МПа, fсd = 20 МПа.

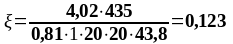


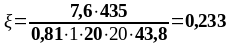
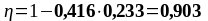
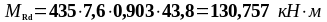
Подбор нижней продольной арматуры во втором пролете:
As2 = 3,08 см2, As1 = 4,02 см2 ,b = 200 мм, , К2 = 0,416, fyd = 435 МПа, fсd = 20 МПа.
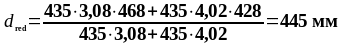
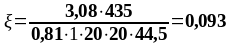
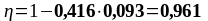
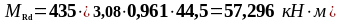
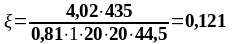
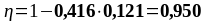
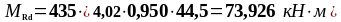
Подбор верхней продольной арматуры на опоре В:
As1 = 4,02 см2, As2 = 7,6 см2,b = 200 мм, , К2 = 0,416, fyd = 435 МПа, fсd = 20 МПа.
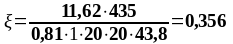
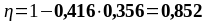
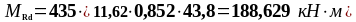
Подбор верхней продольной арматуры на опоре C:
As1 = 4,02 см2, As2 = 4,02 см2,b = 200 мм, , К2 = 0,416, fyd = 435 МПа, fсd = 20 МПа.
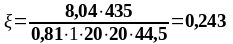
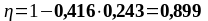
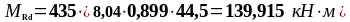
Подбор верхней продольной арматуры в первом и втором пролете:
As1 = 4,02 см2 и As2 = 4,02 см2, b = 200 мм, , К2 = 0,416, fyd = 435 МПа, fсd = 20 МПа.
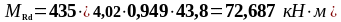
Расчеты, необходимые для построения эпюры материалов сведены в таблицу 2.4.
Анкеровку продольной арматуры определяем в соответствии с [6] (стр.109-112, п.8.4):
Расчетное значение предельного напряжения сцепления fbd для стержней периодического профиля может быть рассчитано следующим образом:
(2.5)
где - расчетное значение предела прочности бетона при растяжении согласно (3.1.6 (2)Р,) [6];
- коэффициент, учитывающий качество сцепления и положение стержней во время бетонирования (рисунок 8.2, стр.110) ( - для хороших условий; - для всех других случаев) [6];
- для ;
(2.6)
где - частный коэффициент безопасности для бетона ( ) (стр.9 табл.2.1N) [6];
- коэффициент, учитывающий влияние длительных эффектов на прочность бетона на растяжение и неблагоприятного способа приложения нагрузки (стр.197, 3.1.6 (2)P) ( ) [6];
- характеристическое значение предела прочности бетона при осевом растяжении (стр.12, табл.3.1) ( ) [6];
Требуемую базовую длину анкеровки lb,rqd для анкеровки усилия Asϭsd в прямом сетржне при постоянном сцеплении fbd определяют по формуле:
(2.7)
где - расчетное напряжение стержня в месте, от которого измеряется анкеровка ( );
- определяют по формуле (2.5);
Расчётная длина анкеровки для сжатых стержней lbd составляет:
(2.8)
где - коэффициент, учитывающий влияние формы стержней при достаточном защитном слое (стр.112, табл.8.2) [6];
- коэффициент, учитывающий влияние минимальной толщины защитного слоя бетона (стр.112, табл.8.2) [6];
- коэффициент, учитывающий влияние усиления поперечной арматурой (стр.112, табл.8.2) [6];
- коэффициент, учитывающий влияние одного или нескольких приваренных поперечных стержней вдоль расчетной длины анкеровки (стр.112, табл.8.2) [6];
- коэффициент, учитывающий влияние поперечного давления плоскости раскалывания вдоль расчетной длины анкеровки (стр.112, табл.8.2) [6];
(2.9)
- определяют по формуле (2.7);
- минимальная длина анкеровки, если не действует другое ограничение принимают:
- для анкеровки при растяжении
(2.10)
- для анкеровки при сжатии
(2.11)
Расчётная длина анкеровки в соответствии с [6] (п.8.4.4 (2) стр.111) для растянутых стержней lb,eq составляет:
(2.12)
Определим по формуле (1.28) расчетное значение предела прочности бетона при растяжении:
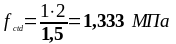
Анкеровка сжатой арматуры
Опора В:
В сечении обрываются стержни Ø22 мм класса S500.
Определим расчетное значение предельного напряжения сцепления по формуле (2.5):
Определим требуемую базовую длину анкеровки по формуле (2.7):
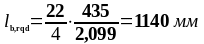
Определим минимальную длину анкеровки по формуле (1.33):

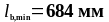
Определим расчётную длину анкеровки по формуле (1.30):
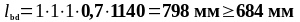
Принимаем
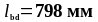 .
.
Опора С:
В сечении обрываются стержни Ø16 мм класса S500.
Определим расчетное значение предельного напряжения сцепления по формуле (1.27):
Определим требуемую базовую длину анкеровки по формуле (1.29):
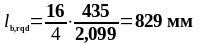
Определим минимальную длину анкеровки по формуле (1.33):
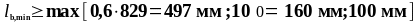
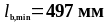
Определим расчётную длину анкеровки по формуле (1.30):
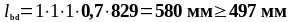
Принимаем
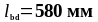 .
.
Анкеровка растянутой арматуры
1-ый пролёт нижняя арматура:
В сечении обрываются стержни Ø22 мм класса S500.
Определим расчетное значение предельного напряжения сцепления по формуле (1.27):
Определим требуемую базовую длину анкеровки по формуле (1.29):
Определим эквивалентную длину анкеровки по формуле (1.34):
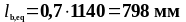
Принимаем
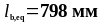 .
.
2-ой пролёт нижняя арматура:
В сечении обрываются стержни Ø16 мм класса S500.
Определим расчетное значение предельного напряжения сцепления по формуле (1.27):
Определим требуемую базовую длину анкеровки по формуле (1.29):

Определим эквивалентную длину анкеровки по формуле (1.34):

Принимаем
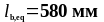 .
.
Эпюра материалов представлена на рисунке 2.7.
Таблица 2.4 - Вычисление ординат эпюры материалов для продольной арматуры
и количество стержней |
dred, см |
As, см2 |
fyd, МПа |
|
|
|
1-й пролет (нижняя арматура, b = 200 мм) |
||||||
2 16 2 22 2 16; 2 22 |
43,8 |
4,02 7,6 11,62 |
435 |
0,123 0,233
|
0,949 0,903
|
72,687 130,757 203,444 |
1-й пролет (верхняя арматура, b = 200 мм) |
||||||
2 16 |
43,8 |
4,02 |
435 |
0,123 |
0,949 |
72,687 |
2-й пролет (нижняя арматура, b = 200 мм) |
||||||
2 14 2 16 2 14; 2 16 |
44,5 |
3,08 4,02 7,1 |
435 |
0,093 0,121
|
0,961 0,950
|
57,296 73,926 131,222 |
2-й пролет (верхняя арматура, b = 200 мм) |
||||||
2 16 |
44,5 |
4,02 |
435 |
0,121 |
0,950 |
73,926 |
Опорная арматура (опора B, b = 200 мм) |
||||||
2 16 2 22 2 16; 2 22 |
43,8 |
11,62 |
435 |
0,356
|
0,852
|
188,629 |
Опорная арматура (опора С, b = 200 мм) |
||||||
2 16 2 16 2 16; 2 16 |
44,5 |
8,04 |
435 |
0,243 |
0,899 |
139,915 |
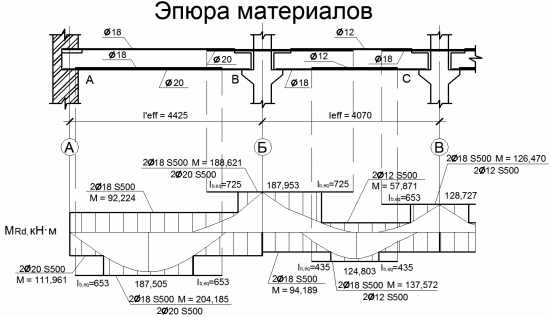
Рисунок 2.7 – Эпюра материалов
2.9 Расчет прочности наклонных сечений по поперечной силе
Расчет производится для сечения у первой промежуточной опоры слева, где действует наибольшая поперечная сила (рисунок 2.5).
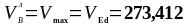 кНм
кНм
Расчет прочности железобетонных элементов на действие поперечных сил начинается в соответствии с п.6.2.1 (3) [6] проверкой условия , где - расчётное значение поперечной силы в сечении, возникающей от внешней нагрузки; - расчётное значение сопротивления поперечной силе элемента без поперечной арматуры определяемое по формуле (1.35) в соответствии с п.6.2.2, (6.2a) (1) [6].
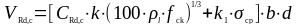 (1.35)
(1.35)
но не менее в соответствии с п 6.2.2, (6.2b) (1) [6]:
(1.36)
где fck= 30 МПа;
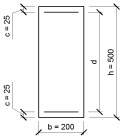
Рисунок 2.8 - К определению рабочей высоты

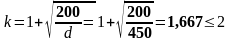
(1.37)
где Asl - площадь сечения растянутой арматуры, которая заведена не менее чем на lbd + d за рассматриваемое сечение (Asl = 11,62 см2);
b – наименьшая ширина поперечного сечения в пределах растянутой зоны (b = 200 мм).
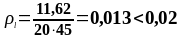
, при отсутствии осевого усилия (сжимающей силы);
- по национальному приложению таблица НП.1, 6.6.4 (1) [6];
- по национальному приложению таблица НП.1, 6.6.4 (1) [6];
- определяем по формуле (1.38) в соответствии с п.6.2.2, (6.3N) (1) [6]
(1.38)
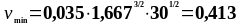
Подставим все значения в формулы (1.35) и (1.36):
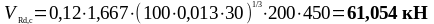
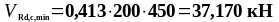
Так
как
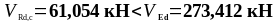 ,
необходим расчёт поперечной арматуры.
,
необходим расчёт поперечной арматуры.
Длина участка, на котором поперечное армирование необходимо устанавливать по расчёту, определяется по эпюре поперечных сил (рисунок 2.9).
Рисунок 2.9 – К расчёту наклонных сечений
Определим расчётный участок:
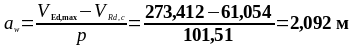
Согласно п.6.2.3 (5) [6] в зонах без скачков и разрывов на эпюре поперечной силы VEd (например, при равномерно распределенной, приложенной по верхней грани элемента нагрузке) площадь поперечной арматуры на любом отрезке длины может быть рассчитана по наименьшему значению VEd в данном отрезке.
Первое расчётное сечение назначим на расстоянии от опоры z1 = d = 450 мм.
Поперечное усилие в данном сечении:
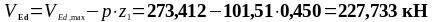
Задаёмся углом наклона к горизонтали .
В пределах длины расчётного участка поперечное армирование рассчитывают из условий:
(1.39)
(1.40)
где - расчетное значение поперечной силы, которая может быть воспринята поперечной арматурой, достигшей текучести, определяем по формуле (1.41) в соответствии с п.6.2.3, (6.8) (3) [6];
- расчетное значение максимальной поперечной силы, которая может быть воспринята элементом, из условия раздавливания сжатых подкосов определяем по формуле (1.42) в соответствии с п.6.2.3, (6.9) (3) [6].
(1.41)
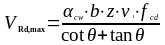 (1.42)
(1.42)
где - площадь сечения поперечной арматуры определяемая по формуле (1.43):
(1.43)
s – расстояние между хомутами;
- расчётное значение предела текучести поперечной арматуры в соответствии с примечанием п.6.2.3, (3) [6] :
- коэффициент понижения прочности бетона, учитывающий влияние наклонных трещин в соответствии с примечанием 1 п.6.2.3, (3) [6]:
- коэффициент, учитывающий уровень напряжения в сжатом поясе в соответствии с примечанием 3 п.6.2.3, (3) [6] ( ).
Плечо внутренней пары сил в соответствии с п.6.2.3 (1) [6]:
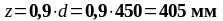
Принимаем шаг хомутов s = 100 мм.
Определим площадь поперечной арматуры по формуле 1.43:
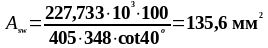
Принимаем по таблице П6 [1] 2ø10 (Asw = 157 мм2).
Максимальная площадь эффективной поперечной арматуры следует из условия п.6.2.3, (6.12) (3) [6]:
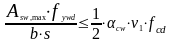 (1.44)
(1.44)
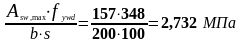
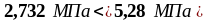
Определим поперечную силу, которая может быть воспринята полосой бетона между наклонными трещинами по формуле (1.42):
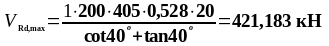
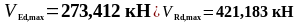
Расстояние от опоры до второго расчётного сечения:
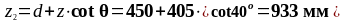
Действующее значение поперечной силы:
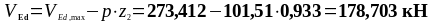
Требуемый шаг поперечной арматуры:
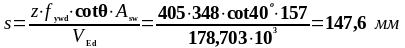
Максимальный шаг поперечной арматуры:

Расстояние от опоры до третьего расчётного сечения:
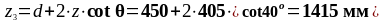
Действующее значение поперечной силы:
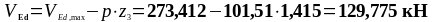
Требуемый шаг поперечной арматуры:
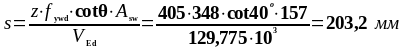
Расстояние от опоры до четвёртого расчётного сечения:
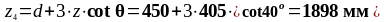
Действующее значение поперечной силы:
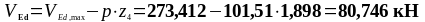
Требуемый шаг поперечной арматуры:
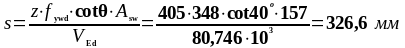
Расстояние от опоры до пятого расчётного сечения:

Действующее значение поперечной силы:
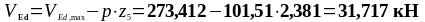
Требуемый шаг поперечной арматуры:
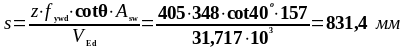
Результаты расчётов сведены в таблицу 2.5
Таблица 2.5 – Шаг стержней поперечной арматуры
Расстояние от опоры до расчётного сечения |
Наименьшее значение поперечной силы в сечении VEd, кН |
Шаг поперечных стержней по расчёту s, мм |
Допустимый шаг, мм |
||||
zi |
мм |
||||||
d |
450 |
227,733 |
115,8 |
100 |
|||
d+z∙cotθ |
933 |
178,703 |
147,6 |
||||
d+2∙z∙cotθ |
1415 |
129,775 |
203,2 |
||||
d+3∙z∙cotθ |
1898 |
80,746 |
326,6 |
300 |
|||
d+4∙z∙cotθ |
2381 |
31,717 |
831,4 |
||||
Таким образом на участке от грани опоры до сечения на расстоянии 1,415 м принят шаг хомутов s1 = 100 мм, а в середине пролёта s2 = 300 мм.
3 Расчет колонны первого этажа
3.1 Исходные данные
В соответствии с табл. 2.1 и пунктом 2.1 вес от сборного перекрытия составит:
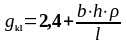 (3.1)
(3.1)
где 2,4 кН/м2 – собственный вес плиты;
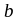 -
ширина ригеля (
);
-
ширина ригеля (
);
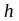 -
высота ригеля (
-
высота ригеля (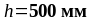 );
);
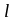 -
пролёт ригеля (
-
пролёт ригеля (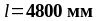 );
);
 -
плотность железобетона (
-
плотность железобетона (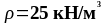 )
)
Подставив все значения в формулу (3.1) получим:
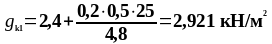
Принимаем вес кровли рулонной трехслойной в соответствии с методическими указаниями [7, стр. 43, табл.17.1]:
gk2= 0,13 кН/м2
Вес утеплителя на покрытии здания в соответствии с методическими указаниями [7, стр. 43, табл.17.2]:
gk3= 1 кН/м2
Вес конструкции пола в соответствии с табл. 2.1 составит:
gk4= 0,72 кН/м2
Нормативная снеговая нагрузка для города Столина (1 снеговой район, подрайон 1в) по национальному приложению изменение №2 ТКП EN 1991-1-3-2009 (стр.4, рисунок НП.1) [8]. Определим снеговую нагрузку действующую на покрытие по следующей формуле ТКП EN 1991-1-3-2009 (стр.6, п.5.2, (5.1)) [9]:
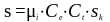 (3.2)
(3.2)
где
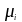 - коэффициент
формы снеговых нагрузок (
- коэффициент
формы снеговых нагрузок ( ),(табл.5.2,
стр.8, п.5.3.2) [9];
),(табл.5.2,
стр.8, п.5.3.2) [9];
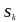 -
характеристическое
значение снеговых нагрузок на грунт
(стр.5, таблица НП.1.1) [8]
-
характеристическое
значение снеговых нагрузок на грунт
(стр.5, таблица НП.1.1) [8]
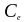 -
коэффициент окружающей среды (стр.7,
п.5.2(7)) [8] (
-
коэффициент окружающей среды (стр.7,
п.5.2(7)) [8] (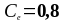 ).;
).;
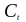 -
температурный коэффициент (стр.7,
п.5.2(8)) [8] (
-
температурный коэффициент (стр.7,
п.5.2(8)) [8] (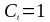 ).
).
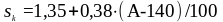 (3.3)
(3.3)
где
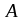 - высота местности над уровнем моря (
- высота местности над уровнем моря ( )
по [10].
)
по [10].
Подставим значения в формулу (3.3):
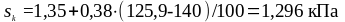
Подставим значения в формулу (3.32):
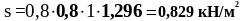
Нормативная временная (полезная) нагрузка на сборное междуэтажное перекрытие qk5 = 6 кН/м2.
Сечение колонн всех этажей здания в первом приближении назначаем 4040 см.
Для определения длины колонны первого этажа Hс1 принимаем расстояние от уровня низа перекрытия первого этажа до обреза фундамента hф = 0,4 м.
Тогда Hс1= Hfl + hф = 4,5 + 0,4 = 4,9 м.
3.2 Подсчет нагрузок
Типовые колонны многоэтажных зданий имеют разрезку через 2 этажа.
При подсчете нагрузок будем рассматривать колонну, размещенную по осям Б-2. Грузовая площадь колонны Агр=4,8х6,8=32,64 м2.
Подсчет нагрузок на колонну выполняем в виде таблицы (табл. 3.1).
Таблица 3.1 - Нагрузки на колонну первого этажа
Наименование и подсчет нагрузок |
Расчётная нагрузка, кН |
Нагрузка от конструкций покрытие:
|
132,225 |
Нагрузка от конструкций перекрытие:
|
356,527 |
Нагрузка от собственного веса колон всех этажей:
|
73,6 |
Временная нагрузка на перекрытие:
|
587,52 |
Снеговая нагрузка на покрытие:
|
27,059 |
Расчетную нагрузку на плиту будем считать по [2] (ст. 59, таблица А.2(А), примечание 2), через сочетание нагрузок, где учитываются постоянные неблагоприятные, доминирующие и прочие сопутствующие воздействия:
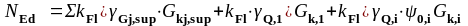 (3.4)
(3.4)
где - коэффициент воздействий, применяемый для дифференциации надёжности по [2] (ст. 59, таблица А.2 (А), примечание 3, );
- частный коэффициент для постоянного воздействия j при определении верхних расчётных значений по [2] (ст. 59, таблица А.2 (А), примечание 2, );
-
верхнее характеристическое значение
постоянного воздействия j
по
таблице
3.1 (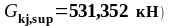 ;
;
- частный коэффициент для доминирующего переменного воздействия по [2] (ст. 59, таблица А.2 (А), примечание 3, );
-
характеристическое значение доминирующего
переменного воздействия
1 по таблице
1.1 (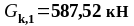 );
);
- частный коэффициент для переменного воздействия I по [2] (ст. 59, таблица А.2 (А), примечание 3, );
-
коэффициент для комбинационного значения
переменного воздействия (стр.6,
п. 4.2 (1), табл. НП.1.2) [8]. (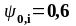 );
);
-
характеристическое значение сопутствующего
переменного воздействия i
по таблице
3.1 (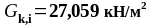 ).
).
Подставив все значения в формулу (1.7) получаем:

3.3 Расчет колонны на прочность
3.3.1 Определение размеров сечения колонны
При продольной сжимающей силе, приложенной со случайным эксцентриситетом, расчёт сжатых элементов с симметричным армированием разрешается производить из следующего условий:
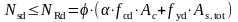
где - коэффициент, учитывающий влияние
продольного изгиба и случайных
эксцентриситетов.
- коэффициент, учитывающий влияние
продольного изгиба и случайных
эксцентриситетов.
Заменив
величину
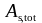 через
через
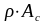 условие
примет вид:
условие
примет вид:
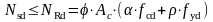
где ρ – коэффициент продольного армирования.
Необходимая
площадь сечения колонны без учёта
влияния продольного изгиба и случайных
эксцентриситетов (e0=ea),
т.е. при
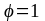 и при эффективном значении ρ=0,2-0,3 для
колонны 1-ого этажа будет равна:
и при эффективном значении ρ=0,2-0,3 для
колонны 1-ого этажа будет равна:
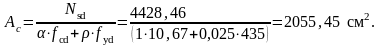
Принимаем
квадратное сечение колонны, размером
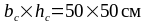 .
Тогда
.
Тогда
 .
.
3.3.2 Расчёт продольного армирования колонны первого этажа
Величина случайного эксцентриситета:
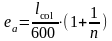 -
в каркасных системах со смещаемыми
узлами для элементов n-го
этажа, считая от верхнего (n=0);
-
в каркасных системах со смещаемыми
узлами для элементов n-го
этажа, считая от верхнего (n=0);
еа =20мм - для сборных элементов, за исключением стен и оболочек;
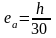 ,
,
где h- высота сечения элемента в плоскости действия расчетного момента.

где l=6+6+1+0,4=13,4м
Принимаем еa=22,33 мм.
Расчётная длина колонны:
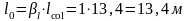
где βl – коэффициент, принимаемый по [4, табл. 6.12].
Условная расчётная длина колонны:

где
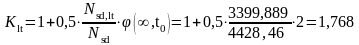
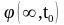 -
предельное значение ползучести бетона,
принимается равным 2,0
-
предельное значение ползучести бетона,
принимается равным 2,0
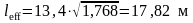
Тогда
гибкость колонны

Отношение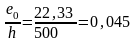
Отсюда
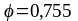 по [3, приложение 15]/
по [3, приложение 15]/
Необходимое сечение продольной арматуры:
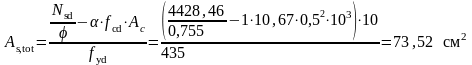
Принимаем836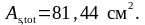
В качестве поперечной арматуры
для армирования колонны принимаем
стержни 10
мм из стали класса S500 см
и устанавливаем с шагом 200мм, что не
превышает 20=20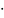 10=200мм
[1, табл.П6].
10=200мм
[1, табл.П6].
3.3.3 Расчет консоли колонны
Консоль колонны воспринимает поперечную силу ригеля от одного междуэтажного перекрытия. Наибольшая поперечная сила действует в сечении 2 слева и равна:
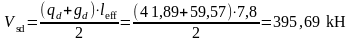 .
.
Минимально допустимая величина опирания ригеля из условия прочности бетона на смятие:
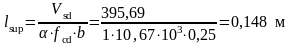
где
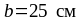 -
ширина ригеля.
-
ширина ригеля.
Принимаем расстояние от торца сборного ригеля до грани колонны =5 см, тогда требуемый вылет консоли равен:
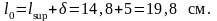
С
учетом возможной неравномерности
распределения давления по опорной
поверхности, а также неточности при
монтаже принимаем
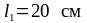 .
При предварительно принятом
.
При предварительно принятом
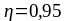 ,
требуемая рабочая высота консоли у
грани колонны из условия прочности
наклонного сечения по сжатой полосе
может быть определена как:
,
требуемая рабочая высота консоли у
грани колонны из условия прочности
наклонного сечения по сжатой полосе
может быть определена как:
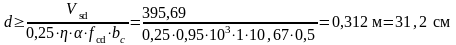
где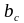 -
размер грани колонны.
-
размер грани колонны.
Полную
высоту консоли у её основания принимаем
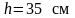 .
.
Тогда
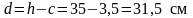
Условие
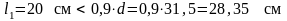 выполняется.
выполняется.
Нижняя грань консоли у ее основания наклонена под углом 450 . Тогда высота свободного конца консоли:
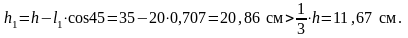
3.3.4Армирование консоли
Ригель опирается на консоль на длине площадки, равной 150 мм, так как зазор между торцом ригеля и гранью колонны принят 50мм, а длины пластины по верху 200 мм.
Расчётный
изгибающий момент силы
 относительно грани колонны:
относительно грани колонны:
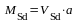 ,
,
где
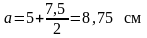 – расстояние от силы
до грани примыкания консоли к колонне.
– расстояние от силы
до грани примыкания консоли к колонне.
 .
.
Требуемую
площадь сечения продольной арматуры
подбираем по изгибающему моменту
 ,
увеличенному на 25%.
,
увеличенному на 25%.
Определяем:
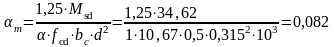
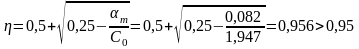
Тогда
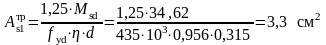
Принимаем
216
S500 с
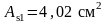 .
Эти стержни привариваются к закладным
деталям консоли.
.
Эти стержни привариваются к закладным
деталям консоли.
При
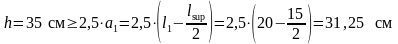 ,
то консоль армируется отогнутыми и
поперечными стержнями.
,
то консоль армируется отогнутыми и
поперечными стержнями.
Площадь сечения отогнутой арматуры можно определить по эффективному коэффициенту армирования:
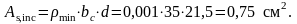
Отогнутую
арматуру устанавливают в двух наклонных
сечениях по два стержня в каждом сечении,
то есть 45
S500 с
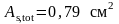 .
Поперечные стержни принимаем по двум
граням консоли из стали S500 25
с
.
Поперечные стержни принимаем по двум
граням консоли из стали S500 25
с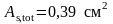 ,устанавливаем
с шагом 50 мм.
,устанавливаем
с шагом 50 мм.
3.3.5 Конструирование стыка ригеля с колонной
Узлы соединения ригелей между собой и с колонной должны обеспечивать восприятие опорных моментов и поперечных сил ригеля. Это достигается соединением опорной арматуры ригеля с помощью стыков и устройством в колоннах опорных консолей или столиков.
Сжимающие усилия в нижней части ригеля передаются через сварные швы, соединяющие закладные детали ригеля и консоли.
Типовым решением является стык с ванной сваркой соединяемых опорных стержней. Именно его примем в данном курсовом проекте. В этом случае ригель и колонна имеют выпуски арматуры, которые свариваются непосредственно или через короткие соединительные стержни. Сжимающие усилия воспринимаются через обетонирование полости стыка.
Стыки с консолями воспринимают значительные моменты и поперечные силы и несложны при исполнении. Они применяются при больших нагрузках, характерных для промышленных зданий.
3.3.6Конструирование стыка колонн
Из условия производства работ стыки колонн назначают на расстоянии 1 м выше перекрытия. При выбранных конструкциях и условиях работы колонны наиболее целесообразным является стык с ванной сваркой продольных стержней.
Для осуществления этого стыка в торцах стыкуемых звеньев колонн в местах расположения продольных стержней устраивают подрезки. Продольные стержни выступают в виде выпусков, свариваемых в медных съемных формах. После сварки стык замоноличивают бетоном того же класса или ниже на одну ступень класса бетона колонны.
Из условия производства работ стыки колонн назначают на расстоянии 1 м выше верхаконсоли. При выбранных конструкциях и условиях работы колонны наиболее целесообразным является стык с ванной сваркой продольных стержней.
Для моноличивания стыка принимаем бетон класса С16/20 и выпуски арматуры длиной 30 см и диаметром 36 мм из стали S500.
Стык рассчитыватся для стадий:
до замоноличивания как шарнирный на монтажные (постоянные) нагрузки,
после замоноличивания как жёсткий с косвенным армированием на эксплуатационные (полные) нагрузки.
Размеры
сечения подрезки из условия размещения
медных форм принимаем
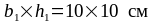 ,
а расстояние от грани сечения до оси
сеток косвенного армирования в пределах
подрезки
,
а расстояние от грани сечения до оси
сеток косвенного армирования в пределах
подрезки
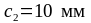 ;
за пределами подрезки
;
за пределами подрезки
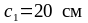 .
.
Центрирующую
прокладку и распределительные листы в
торцах колонн назначаем толщиной 2 см,
а размеры в плане: центрирующей прокладки
-
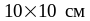 ,
что не превышает 1/4 ширины колонны,т.е.,
1/4∙50=12,5см, распределительных листов
,
что не превышает 1/4 ширины колонны,т.е.,
1/4∙50=12,5см, распределительных листов
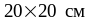 .
.
Сварные
сетки конструируем из проволоки Ø5 S500
с fyd
= 417 МПа и
 см2.
Размеры ячеек сетки должны быть не менее
45 мм, не более 1/4×bк
и не более 100 мм. Принимаем шаг 70 мм.
см2.
Размеры ячеек сетки должны быть не менее
45 мм, не более 1/4×bк
и не более 100 мм. Принимаем шаг 70 мм.
Шаг сеток следует принимать не более 150 мм и не более 1/3 стороны сечения. Шаг сеток с учетом ограничения принимаем 70 мм.
Список использованных источников
Волик А.Р., Гаврильчик М.Н. Методические указания к выполнению курсового проекта «Многоэтажное каркасное здание» (Монолитное железобетонное ребристое перекрытие) – (электронная версия).
СНБ 5.03.01–02. «Конструкции бетонные и железобетонные». – Мн.: Стройтехнорм, 2002 г. – 274 с.
Волик А.Р. Методические указания к выполнению курсового проекта «Многоэтажное каркасное здание» (Сборный вариант) – (электронная версия).
Железобетонные конструкции. Основы теории, расчёта и конструирования/ Под ред. Пецольда Т. М. и Тура В. В. – Брест: БрГТУ, 2003. – 380 с.
Нагрузки и воздействия: СНиП 2.01.07-85.–М.:1987.–36c.

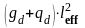
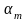
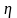
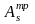 ,
,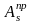 ,
,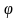 12
12