3.5 Исследование трёхфазных электрических цепей
при соединении приёмников «звездой»
Основные теоретические положения
Объектом исследования являются трёхфазные электрические цепи, схемы которых приведены на рис.3.21 и рис.3.24
Провода, соединяющие фазы генератора и нагрузки, называются линейными. Рассматривается случай, когда сопротивлениями линейных проводов можно пренебречь. На схеме показаны условные положительные направления токов и напряжений. Напряжения между началом и концом фазы называются фазными. Напряжения между любыми двумя линейными проводами – линейными. Напряжение между нулевыми точками приемника и генератора – напряжением смещения. Токи в фазах называются фазными токами, а токи в линейных проводах – линейными. Из схем видно, что при соединении нагрузки «звездой», линейные токи равны фазным.
На рис. 3.21 представлена трехфазная цепь с нулевым или нейтраль-ным проводом. Нейтральным называется провод, соединяющий нулевые точки генератора N и приемника n . Рассматривается случай, когда сопротивлением нейтрального провода ZN можно пренебречь. В этом случае точки N и n имеют одинаковый потенциал. Ток, протекающий в нейтральном проводе, называется нейтральным или нулевым.
В общем случае, для определения токов IА, IВ и IС при заданных ЭДС генератора и сопротивлениях фаз, можно применить метод двух узлов.
В
соответствии с этим методом определяется
напряжение смещения:
,
(1)
где
комплексные
источни ки
ЭДС
трёхфазного генератора;
комплексные проводимости фаз
нагрузки.
Рис.3.21 Трёхфазная
электрическая цепь без нейтрального
провода
Фазные токи нагрузки определяются следующими соотношениями:
(2)
При этом
должно
выполняться условие:
В настоящем исследовании комплексные проводимости каждой фазы являются вещественными, т.к. нагрузкой фаз являются резисторы:
Расчет фазных и
линейных напряжений
на нагрузке определяется
соотношениями:
(3)
(4)
На рис. 3.22 и 3.23 приведены лучевая векторная диаграмма токов и векторно-топографическая диаграмма напряжений для схемы изображенной на рис.3.21 для общего случая нагрузки.
. Рис.3.22 Лучевая
векторная
диаграмма токов
. Рис.3.23
Векторно-топографическая
диаграмма напряжений
Особенности расчёта в зависимости от нагрузки
Симметричная нагрузка
При симметричной нагрузке: Ra = Rв= Rс =R
При
использовании формулы (1) напряжение
смещения ŮnN=0,
т.к. для симметричного генератора
выполняется условие:
Несимметричная нагрузка
При несимметричной нагрузке:Ra ≠ Rв ≠ Rс
Обрыв одной из фаз нагрузки
Сопротивление такой фазы приравнивается к бесконечности, а проводимость – к нулю. При вычислении фазного напряжения в обрыве фазы следует воспользоваться второй формой соотношения в уравнении (3)
Короткое замыкание фазы
Сопротивление такой фазы приравнивается к нулю, а проводимость – к бесконечности. Напряжение смещения в этом случае соответствует источнику ЭДС короткозамкнутой фазы, т.е. при Rа = 0 ŮnN =ĖA ; при Rв = 0 ŮnN = ĖВ ; при Rс = 0 ŮnN = ĖС.
Ток короткозамкнутой фазы определяется из уравнения по первому закону Кирхгофа: İА + İВ + İС = 0
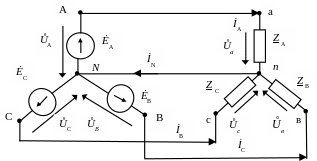
Рис.3.24
Трёхфазная
электрическая цепь с нейтральным
проводом
Напряжение смещения
в данном случае
ŮnN
=
0.
Фазные
токи нагрузки определяются следующими
соотношениями:
(5)
Ток в нейтральном
проводе определяется при помощи первого
закона Кирхгофа:
Фазные и линейные напряжения на нагрузке равны соответствующим фазным и линейным напряжениям генератора:
На
рис.
3.25 и 3.26 приведены лучевая векторная
диаграмма токов
векторно-топографическая
диаграмма
напряжений
для
схемы изображенной
на рис. 3.24 для общего
случая
нагрузки.
Рис.3.25
Лучевая
векторная
диаграмма
токов
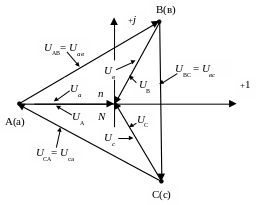
Рис.3.26
Векторно-топографическая
диаграмма напряжений
При проверке баланса мощностей определяется комплексная мощность трехфазного источника питания:
где
- сопряжённые
комплексные токи
Комплексная
мощность
трехфазной нагрузки определяется
соотношением: