Тема 4. Схема Бернулли
Задача 1. Правильная игральная кость бросается 4 раза. Какова вероятность того, что грань с шестёркой выпадет хотя бы два раза?
Задача 2. Контрольная работа состоит из 4-х тестовых вопросов. На каждый из вопросов приведено 3 варианта ответа, среди которых только один правильный. За каждый правильный ответ начисляется 1 балл. Какова вероятность того, что при выборе наугад ответа на каждый вопрос, студент получит хотя бы 3 балла?
Задача 3. Какая вероятность больше: выиграть у равносильного соперника (например, в шахматы) 3 партии из 4-х или 5 партий из 8-ми? (Ничьи не учитывать).
Тема 5. Вычисление математического ожидания и дисперсии
Задача 1. За неделю цены на один и тот же товар повысились в 30% торговых точек. Случайно были отобраны 10 торговых точек. Каковы ожидаемое число (математическое ожидание) и стандартное отклонение в этой выборке числа торговых точек, в которых цены повысились?
Задача 2. Правильную монету бросили 50 раз. Найдите математическое ожидание и дисперсию числа выпавших гербов.
Задача 3. Правильную игральную кость бросили 12 раз. Найдите математическое ожидание и дисперсию числа выпавших шестёрок.
Задача 4. Для независимых случайных величин X и Y отметьте правильные варианты преобразований дисперсии :
Задача 5. У студента в связке 3 ключа, внешне неразличимые, но только один из них подходит к замку двери квартиры. Чтобы открыть дверь в квартиру, он случайным образом выбирает ключ из связки. Если ключ не подошёл к замку, попытка повторяется. При этом не подошедший ключ в дальнейших попытках не участвует. Найдите распределение числа попыток открытия двери. Найдите математическое ожидание этого распределения.
Задача 6. Студент может поехать на занятия или на автобусе, или на маршрутке. Вероятность поездки на маршрутке в 2 раза больше, чем на автобусе. Билет на автобус стоит 30 руб., а на маршрутку – 45 руб. Найти математическое ожидание и дисперсию стоимости одной поездки на транспорте.
Тема 6. Нормальное распределение.
Используя таблицу для функции распределения стандартной нормальной величины, вычислите следующие вероятности.
Задача
1. Пусть
случайная величина Z
имеет стандартный нормальный закон
распределения, т.е.
Найти:
1)
2)
3)
4)
5)
6)
7)
8)
Задача
2. Пусть
случайная величина X
имеет нормальный закон распределения
с математическим ожиданием m
и дисперсией
,
т.е.
(В каждой задаче величины m
и
заданы.)
Найти:
1)
Пусть
2)
Пусть
3)
Пусть
4)
Пусть
5)
Пусть
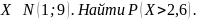
Задача
3.
Есть акции 2-х компаний. Их ежедневные
цены на бирже X
и Y
имеют нормальное распределение со
средним 100 руб. и стандартным отклонением
5 руб. и независимы. Один инвестор купил
на 200 руб. акции первой компании, второй
– на те же деньги акцию первой и акцию
второй компаний. Найти вероятности:
и
.
У какого инвестора вероятность понести
убытки меньше ?
Задача 4. Рост девушек-студенток распределён по нормальному закону с математическим ожиданием 168 см. и дисперсией 36 см2. Выбираем случайным образом двух девушек. Какова вероятность того, что хотя бы одна из двух девушек имеет рост, меньше 165 см.?
Задача 5. В магазин поступила большая партия пачек печенья. Вес пачки печенья – случайная величина, распределённая по нормальному закону с математическим ожиданием 200 г. и дисперсией 49 г2. Случайно выбираем 2 пачки печенья. Какова вероятность того, что хотя бы одна пачка имеет вес меньше 192 г.
Задача 6. Прибор, измеряющий скорость автомобилиста, имеет погрешность, которая распределена по нормальному закону с нулевым математическим ожиданием (т.е. без систематической ошибки) и стандартным отклонением 2 км/час. Автомобилист будет оштрафован, если прибор зафиксирует скорость, которая превышает допустимую на данном участке скорость на 20 км/час. Какова вероятность того, что автомобилист, превысивший скорость на 22 км/час не будет оштрафован по замерам этого прибора? Какова вероятность того, что автомобилист, превысивший скорость на 18 км/час будет оштрафован по замерам этого прибора?