Развитие методов записи и хранения данных привело к бурному росту объемов собираемой и анализируемой информации. Объемы данных настолько внушительны, что человеку просто не по силам проанализировать их самостоятельно, хотя необходимость проведения такого анализа вполне очевидна, ведь в этих "сырых" данных заключены знания, которые могут быть использованы при принятии решений. Для того чтобы провести автоматический анализ данных, используется Data Mining.

Data Mining – это процесс обнаружения в "сырых" данных ранее неизвестных нетривиальных практически полезных и доступных интерпретации знаний, необходимых для принятия решений в различных сферах человеческой деятельности. Data Mining является одним из шагов Knowledge Discovery in Databases.

Информация, найденная в процессе применения методов Data Mining, должна быть нетривиальной и ранее неизвестной, например, средние продажи не являются таковыми. Знания должны описывать новые связи между свойствами, предсказывать значения одних признаков на основе других и т.д. Найденные знания должны быть применимы и на новых данных с некоторой степенью достоверности. Полезность заключается в том, что эти знания могут приносить определенную выгоду при их применении. Знания должны быть в понятном для пользователя не математика виде. Например, проще всего воспринимаются человеком логические конструкции "если … то …". Более того, такие правила могут быть использованы в различных СУБД в качестве SQL-запросов. В случае, когда извлеченные знания непрозрачны для пользователя, должны существовать методы постобработки, позволяющие привести их к интерпретируемому виду.

Алгоритмы, используемые в Data Mining, требуют большого количества вычислений. Раньше это являлось сдерживающим фактором широкого практического применения Data Mining, однако сегодняшний рост производительности современных процессоров снял остроту этой проблемы. Теперь за приемлемое время можно провести качественный анализ сотен тысяч и миллионов записей.

Задачи, решаемые методами Data Mining:

1. Классификация – это отнесение объектов (наблюдений, событий) к одному из заранее известных классов.

2. Регрессия, в том числе задачи прогнозирования. Установление зависимости непрерывных выходных от входных переменных.

3. Кластеризация – это группировка объектов (наблюдений, событий) на основе данных (свойств), описывающих сущность этих объектов. Объекты внутри кластера должны быть "похожими" друг на друга и отличаться от объектов, вошедших в другие кластеры. Чем больше похожи объекты внутри кластера и чем больше отличий между кластерами, тем точнее кластеризация.

4. Ассоциация – выявление закономерностей между связанными событиями. Примером такой закономерности служит правило, указывающее, что из события X следует событие Y. Такие правила называются ассоциативными. Впервые эта задача была предложена для нахождения типичных шаблонов покупок, совершаемых в супермаркетах, поэтому иногда ее еще называют анализом рыночной корзины (market basket analysis).

Проблемы бизнес анализа формулируются по-иному, но решение большинства из них сводится к той или иной задаче Data Mining или к их комбинации. Например, оценка рисков – это решение задачи регрессии или классификации, сегментация рынка – кластеризация, стимулирование спроса – ассоциативные правила. Фактически, задачи Data Mining являются элементами, из которых можно собрать решение подавляющего большинства реальных бизнес задач.

Для решения вышеописанных задач используются различные методы и алгоритмы Data Mining. Ввиду того, что Data Mining развивалась и развивается на стыке таких дисциплин, как статистика, теория информации, машинное обучение, теория баз данных, вполне закономерно, что большинство алгоритмов и методов Data Mining были разработаны на основе различных методов из этих дисциплин. Например, процедура кластеризации k-means была просто заимствована из статистики. Большую популярность получили следующие методы Data Mining: нейронные сети, деревья решений, алгоритмы кластеризации, в том числе и масштабируемые, алгоритмы обнаружения ассоциативных связей между событиями и т.д.

Deductor является аналитической платформой, в которую включен полный набор инструментов для решения задач Data Mining: линейная регрессия, нейронные сети с учителем, нейронные сети без учителя, деревья решений, поиск ассоциативных правил и множество других. Для многих механизмов предусмотрены специализированные визуализаторы, значительно облегчающие использование полученной модели и интерпретацию результатов. Сильной стороной платформы является не только реализация современных алгоритмов анализа, но и обеспечение возможности произвольным образом комбинировать различные механизмы анализа.

Опыт построения математической модели синдрома цитолиза при инфекционном мононуклеозе у детей

Цель исследования

Определение возможности применения различных статистических и аналитических методов для построения прогностической модели синдрома цитолиза при инфекционном мононуклеозе у детей.

Материалы и методы

Для построения математической модели синдрома цитолиза при мононуклеозе были использованы следующие методы:

- статистические - корреляция, логистическая регрессия;

- интеллектуальный анализ данных DataMining(построение ассоциативных правил, деревьев решений и искусственных нейронных сетей).

Анализ производился при помощи программ Biostat 2009, DeductorStudio, входящей в аналитическую платформу DeductorLite, разработанной в фирме BaseGroupLabs.

В качестве материала для исследования были использованы данные 46 наблюдений случаев острого мононуклеоза, потребовавших госпитализации в инфекционное отделение детской больницы.

Для построения математической модели, с целью упрощения расчетов, были выбраны только 8 критериев объективного и клинического обследования:

- гепатоспленомегалия;

- лимфаденопатия;

- острый тонзиллит (ангина);

- лейкоцитоз периферической крови (значения выше 13*10*9)

- атипичные мононуклеары в периферической крови (более 10);

- серопозитивностьIg М к ВЭБ;

-серопозитивностьIg Мк ЦМВ.

Первичные данные были занесены в электронную таблицу, причем условия в форме «да-нет» были закодированы числами (1- да, 0 – нет), таким образом, для анализа использовалось содержимое 368 ячеек (таблица размером 46*8).

Результаты и обсуждение:

Есть два подхода к анализу данных с помощью информационных систем.

В первом варианте программа используется для визуализации информации – извлечения данных из источников и предоставления их человеку для самостоятельного анализа и принятия решений. Обычно данные, предоставляемые программой, являются простой таблицей.

Второй вариант использования программного обеспечения для анализа – это построение моделей. Модель имитирует некоторый процесс. Для построения модели необходимо сделать предобработку данных и далее к ним применять математические методы анализа:кластеризацию, классификацию, регрессию и т. д. Построенную модель можно использовать для принятия решений, объяснения причин, оценки значимости факторов, моделирования различных вариантов развития.

В своем исследовании мы попытались построить модель развития синдрома цитолиза при инфекционном мононуклеозе у детей.

1. Определение распространенности изучаемых синдромов.

Согласно простых математических расчетов, изучаемые синдромы в исследуемой выборке из 46 наблюдений распределились следующим образом (рис 1):

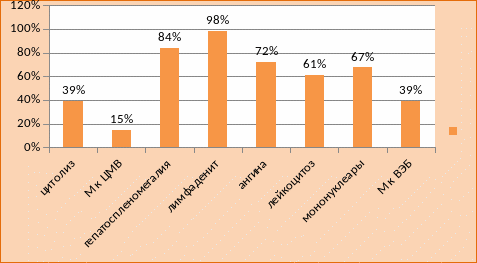
Рис.1 Распространенность синдромов острого мононуклеоза у детей.

Синдром цитолиза в исследуемой выборке встречался в 39% случаев.

2. Корреляционный анализ. Вычисление коэффициента корреляции Пирсона.С помощью метода корреляционного анализа были вычислены попарные коэффициенты корреляции каждого из изучаемых синдромов (рис. 2). Полученные значения коэффициентакорреляции Пирсона (от -0,08 до 0,2) свидетельствуют о наличии слабых и разнонаправленных связей между изучаемыми признаками. То есть, обнаруженные на этом этапе анализа закономерности никак не могут быть использованы в практическом здравоохранении.

Рис. 2 Матрица попарных коэффициентов корреляции Пирсона.

На следующем этапе своего исследования мы применяли методы интеллектуального анализа данных, а именно DataMining.

DataMining – это процесс обнаружения в "сырых" данных ранее неизвестных нетривиальных практически полезных и доступных интерпретации знаний, необходимых для принятия решений в различных сферах человеческой деятельности.

DataMining чаще всего решает четыре задачи — ассоциация, кластеризация, классификация и регрессия.

Ассоциация – выявление зависимостей между связанными событиями, указывающих, чтоиз события X следует событие Y. Такие правила называются ассоциативными.

Кластеризация – это группировка объектов (наблюдений, событий) на основе данных(свойств), описывающих сущность объектов. Объекты внутри кластера должны быть«похожими» друг на друга и отличаться от объектов, вошедших в другие кластеры. Чембольше похожи объекты внутри кластера и чем больше отличий между кластерами, темточнее кластеризация.

Классификация – установление функциональной зависимости между входными идискретными выходными переменными. При помощи классификации решается задачаотнесение объектов (наблюдений, событий) к одному из заранее известных классов.

Регрессия – установление функциональной зависимости между входными и непрерывнымивыходными переменными. Прогнозирование чаще всего сводится к решению задачирегрессии.

3. Линейный регрессионный анализ.

Данный метод позволяет строить линейные зависимости между наборами объясняемых и объясняющих переменных. Задача линейной регрессии заключается в нахождении коэффициентов уравнения линейной регрессии, которое имеет вид:

y = 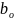+ +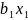 +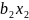…+ 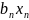(1.1)

где у – выходная (зависимая) переменная модели;

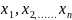– входные (независимые) переменные

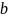- коэффициенты линейной регрессии, называемые также параметрами модели ( - свободный член).

Задача линейной регрессии заключается в подборе коэффициентов 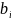уравнения (1.1) таким образом, чтобы на заданный входной вектор Х=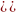 ) регрессионная модель формировала желаемое выходное значение у.

В нашем случае входными переменными модели 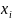являются изучаемые синдромы, а у – прогнозируемое значение – цитолиз (есть- true, нет- false). В нашем случае выходная переменная является бинарной (может принимать только два значения), поэтому необходимо использовать специальную модификацию – логистическую регрессию, предназначенную для предсказания зависимой переменной, принимающей значение в интервале от 0 до 1, то есть на выходе модели могут появляться только два значения: 1- цитолиз есть (true) , 0 – цитолиза нет (false) . В этом случае задача прогнозирования фактически сводится к классификации, а именно к разделению пациентов на две группы. К первой группе будут отнесены пациенты, для которых прогноз развития синдрома цитолиза положительный, а ко второй группе – пациенты, для которых прогноз отрицательный. Логистическая регрессия служит не для предсказания значений зависимой переменной, а скорее для оценки вероятности того, что зависимая переменная примет заданное значение.

Анализ производился при помощи программы DeductorStudio. В визуализаторе «отчет по регрессии» оценивается статистическая значимость всей модели, а также каждого регрессионного коэффициента в отдельности (рис. 3)

Рис 3. Отчет логистической регрессии.

Помимо коэффициента для каждой регрессионной переменной в таблице рассчитывается отношение шансов (oddsratio) и балл – переведенное в линейную шкалу отношение шансов.

Отношение шансов OR – это отношение вероятности того, что событие произойдет к вероятности того, что событие не произойдет: OR = p / (1 – p), где p – вероятность успеха.

В нашем примере категориальный признак «печень+» имеет два веса: 1 при[отрицательная, нет] и 3,04 – при [положительная]. Это значит, что при наличии у больного синдрома гепатоспленомегалии («печень+») шансы развития синдрома цитолиза в 3 раза выше по сравнению с другими.

Качество произведенной классификации методом логистической регрессии оценено следующим образом:

- чувствительность (мера вероятности того, что любой случай будет идентифицирован с помощью модели) - составила 88%.

Рис.4 Качество классификации.