Первая (основная) форма уравнений равновесия:
ТЕОРЕМА С11. Для того, чтобы плоское тело находилось в равновесии, необходимо и достаточно, чтобы сумма моментов всех сил относительно двух различных произвольно выбранных точек была равна нулю и сумма проекций сил относительно любой оси, не перпендикулярной линии, соединяющей эти две точки, тоже была равна нулю.
Без доказательства.
Вторая форма уравнений равновесия (ось х не перпендикулярна AB):
ТЕОРЕМА С12. Для того, чтобы плоское тело находилось в равновесии, необходимо и достаточно, чтобы сумма моментов всех сил относительно трех различных произвольно выбранных точек, не лежащих на одной прямой, была равна нулю.
Без доказательства.
Третья форма уравнений равновесия (А, В и С не лежат на одной прямой):
СТАТИЧЕСКАЯ ОПРЕДЕЛИМОСТЬ
Если количество неизвестных в задаче равняется количеству уравнений равновесия, то такая задача называется СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ, если больше, то СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ, если меньше - СТАТИЧЕСКИ ПЕРЕОПРЕДЕЛЕННОЙ. На рис. 7 показана конструкция, которая будет статически определимой, а на рис. 8 – статически неопределимой.
В СТАТИКЕ РЕШАЮТСЯ ТОЛЬКО СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ ЗАДАЧИ.
Из определения понятия состояния покоя следует, что если вся конструкция находится в покое, то и любая ее часть также находится в состоянии покоя. Поэтому для любой части конструкции также можно составлять уравнения равновесия, учитывая при этом, что отброшенная часть конструкции является связью. Разрывать конструкцию следует не в произвольных местах, а там, где имеются внутренние не жесткие связи (например, шарнир внутри конструкции, ползун на направляющей и т.д.). Каждая такая не жесткая связь снимает одну или несколько (в зависимости от конструктивных особенностей) степеней статической неопределимости. В частности шарнир снимает одну степень статической неопределимости.
Если приходится рассматривать равновесие двух взаимодействующих частей конструкции, то следует учитывать, что согласно аксиоме С5 силы их воздействия друг на друга равны по величине, лежат на одной прямой и противоположно направлены.
СИСТЕМА ПАРАЛЛЕЛЬНЫХ СИЛ
Система сил, линии действия которых параллельны, называются СИСТЕМОЙ ПАРАЛЛЕЛЬНЫХ СИЛ.
ЛЕММА 1. Две параллельные силы всегда имеют равнодействующую.
Доказательство.
Рассмотрим две параллельные силы
и
(рис.16а). Выберем некоторую точку А,
лежащую между линиями действия этих
сил, причем соответствующие расстояния
и
связаны следующей пропорцией
.
Рис. 16
Перенесем
силы
и
параллельно
самим себе в точку А.
Согласно теореме С7, мы получим
результирующую
и пару сил с моментом
.
Но правая часть выражения для момента
в силу выбора точки А
будет равна нулю, т.е. момент будет
отсутствовать, а значит
будет действительно равнодействующей
(рис. 16б). Если силы будут направлены в
разные стороны, то доказательство
сохраняется с маленьким изменением:
точку А
надо выбирать не между линий действия,
а со стороны меньшей силы.
ТЕОРЕМА С13. Система параллельных сил всегда имеет равнодействующую.
Доказательство. Очевидно, что, применяя лемму 1 к любым двум силам системы, мы получим из системы n сил систему n-1 сил. Повторив эту процедуру n-1 раз, мы наверняка получим только одну силу, заменяющую всю систему, т.е. равнодействующую.
Равнодействующая приложена к определенной точке, называемой ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ.
Координата центра параллельных сил
Рассмотрим систему , , ..., параллельных сил (рис. 17). Заметим, что силы могут быть направлены и в противоположные стороны. Выберем систему координат таким образом, чтобы одна из осей была перпендикулярна линиям действия этих сил (ось X на рис. 17).
Рис. 17
Подсчитаем суммарный момент этих сил относительно начала координат (в приводимой формуле оперируем величинами сил)
.
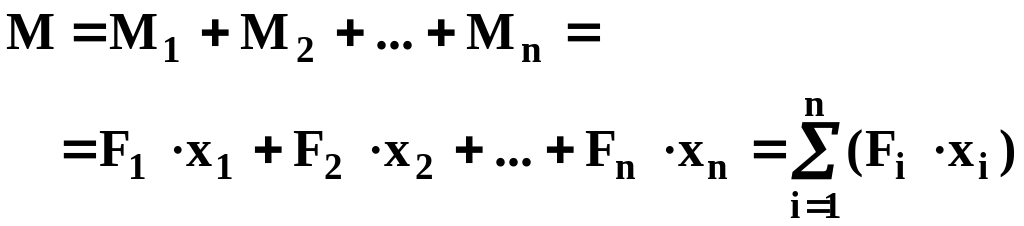Но на основании теоремы С13 мы знаем, что эти силы имеют равнодействующую, поэтому, согласно теореме С5 (теорема Вариньона), этот момент должен быть равен моменту равнодействующей относительно начала координат
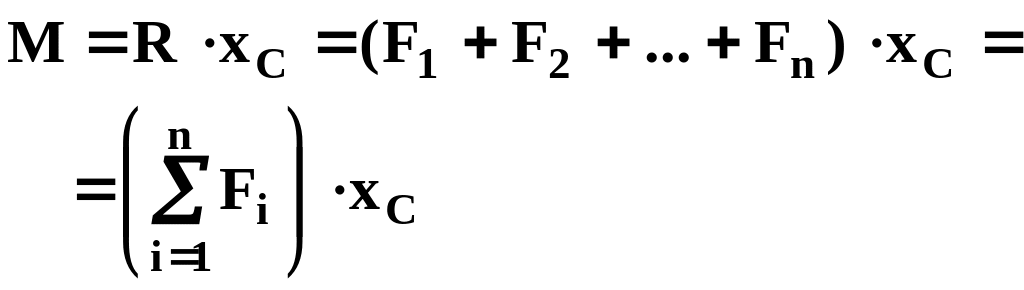
следовательно, приравняв эти моменты, получим
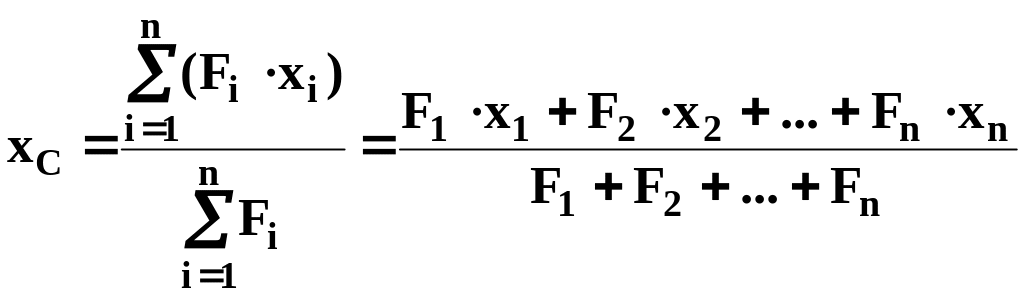
По другим осям координат выражение получится точно таким же, только в правой части надо соответственно заменить х на у или z. Следовательно, можем записать полученную зависимость в векторной форме
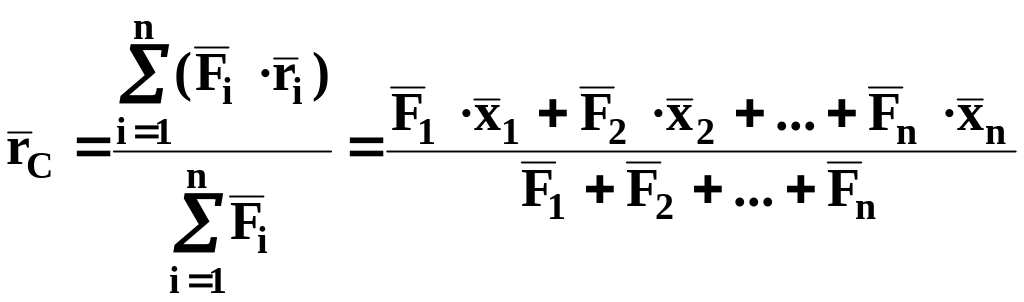
Заметим, что, если повернуть все силы на один и тот же угол (рис. 18), а систему координат оставить на месте, то, повторив вывод формулы, получим то же самое значение, т.е. относительное положение центра параллельных сил не зависит от выбора системы координат.
Рис. 18