Движение под действием центральной силы

ЦЕНТРАЛЬНАЯ СИЛА – это сила, линия действия которой проходит через одну и ту же неподвижную точку в выбранной системе координат.

Рассмотрим движение точки М, на которую действует центральная сила направленная всё время в точку O (рис. 4). Поскольку линия действия силы пересекает точку O , то момент силы относительно точки O всегда равен нулю и согласно теореме Д13

Рис. 6.

Если траектория – плоская кривая, то

Пусть . Поскольку модуль скорости пропорционален длине элементарной дуги траектории dS, то можно считать, что = const. С небольшой степенью погрешности можно считать, что площадь заштрихованного на рис. 6 треугольника

Величина  называется СЕКТОРИАЛЬНОЙ ПЛОЩАДЬЮ.

МАТЕРИАЛЬНАЯ ТОЧКА ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ ДВИЖЕТСЯ ТАКИМ ОБРАЗОМ, ЧТО СЕКТОРИАЛЬНАЯ ПЛОЩАДЬ, ОПИСЫВАЕМАЯ ЕЮ ЗА РАВНЫЕ ПРОМЕЖУТКИ ВРЕМЕНИ, БУДЕТ ОДИНАКОВА. Получается, что вблизи от точки O материальная точка будет двигаться с относительно большой скоростью, а вдали – с маленькой. Это действительно наблюдается при движении космических объектов по вытянутым эллиптическим орбитам.

Уравнение вращательного движения тела

Если рассматривается вращательное движение одного тела, то, подставив (52) в (55а), получим

Так как J = const, то

Поскольку производная от угловой скорости – это угловое ускорение (КИНЕМАТИКА стр.9), то окончательно имеем

(56)

Уравнения плоскопараллельного движения тела

Как известно из кинематики (КИНЕМАТИКА стр. 11), плоскопараллельное движение можно представлять как выполнение телом одновременно и поступательного и вращательного движения. Поэтому уравнения движения для этого случая должны включать уравнения аналогичные и (43), и (56). Проще всего уравнения получаются, если в качестве полюса выбирать центр масс тела. Кроме того, выберем систему координат таким образом, что оси X и Y лежали в плоскости движения, а ось Z перпендикулярна ей. Тогда уравнения движения могут быть выражены в проекциях в следующем виде

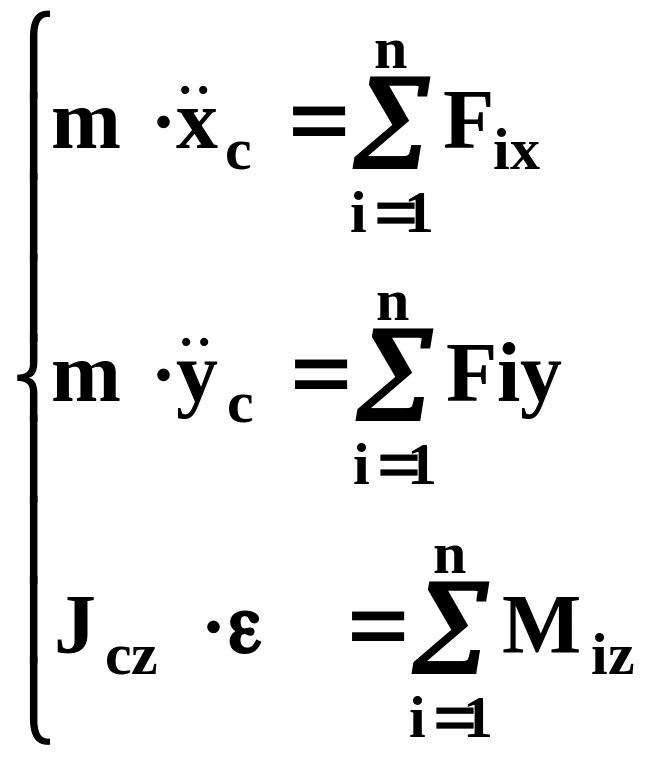(57)

где x_c и y_c - координаты центра масс тела;

J_cz - собственный момент инерции тела относительно оси, перпендикулярной плоскости движения.

Кинетическая энергия механической системы

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ МАТЕРИАЛЬНОЙ ТОЧКИ – это половина произведения массы точки на её скорость

(58)

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ – это сумма кинетических энергий всех точек системы

ТЕОРЕМА Д14. Кинетическая энергия тела, которое движется плоскопараллельно, равна сумме массы тела, умноженной на половину квадрата скорости центра масс тела и половине произведения собственного момента инерции тела на квадрат угловой скорости.

Доказательство. Рассмотрим движение тела, которое движется плоскопараллельно. Выберем в качестве полюса центр масс тела. Тогда скорость любой точки тела можно выразить (КИНЕМАТИКА стр. 9)

где скорость центра масс тела;

угловая скорость тела;

расстояние от i-й точки до центра масс.

Кинетическая энергия будет выражена

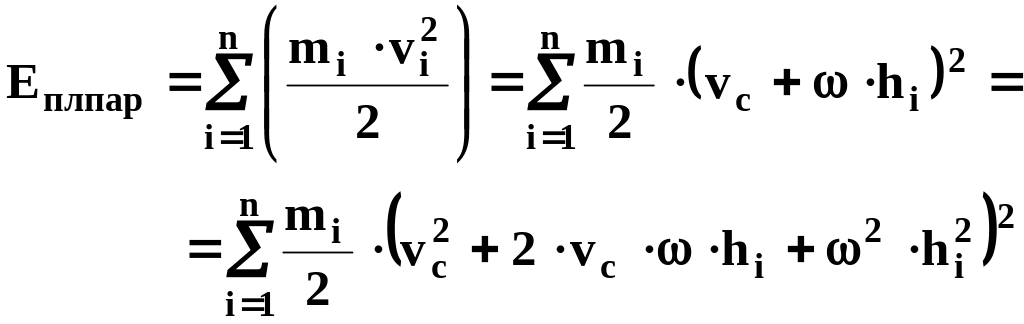
Используя свойства суммирования и вынеся из-под знака суммирования постоянные величины, получим

с учетом (40) и (48), окончательно имеем

ч.т.д. (59)

Следствие 1. При поступательном движении тела его кинетическая энергия равна половине произведения массы тела на квадрат скорости любой точки тела.

Действительно, поступательное движение можно считать частным случаем плоскопараллельного при отсутствии вращения (КИНЕМАТИКА стр. 12), т.е. при . Кроме того, при поступательном движении скорости всех точек тела равны. Тогда из (59)

(60)

Следствие 2. При вращательном движении тела его кинетическая энергия равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости.

Действительно, пусть тело вращается относительно оси, находящейся на расстоянии b от центра масс тела. Тогда скорость центра масс (КИНЕМАТИКА стр. 9) можно выразить . Из формулы (59) будем иметь

(61)

Выражение в скобках, согласно теореме Д9, есть не что иное, как момент инерции относительно действительной оси вращения.

РАБОТА

ЭЛЕМЕНТАРНАЯ РАБОТА СИЛЫ – это скалярное произведение силы на вектор элементарного перемещения точки приложения силы.

(62)

где угол между направлением действия силы и направлением элементарного перемещения.

Из последней формулы видно, что

- если направления силы и перемещения совпадают, то работа равна просто произведению силы на перемещение;

- если направления силы и перемещения перпендикулярны друг другу, то работа равна нулю;

- если угол между силой и перемещением больше прямого угла, то работа силы будет величиной отрицательной.

Полная РАБОТА СИЛЫ на конечном перемещении – это сумма всех элементарных работ данной силы

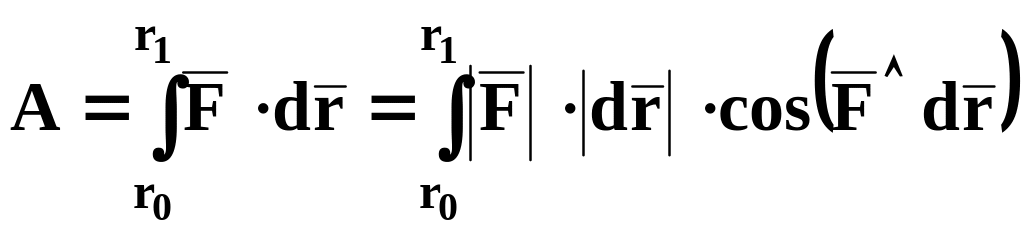(63)

Приведем несколько случаев определения работ для разного вида сил. Для простоты будем считать, что сила и перемещение совпадают по направлению. Если это в задаче не так, то результат надо просто умножить на косинус соответствующего угла.