6 Пример выполнения индивидуального задания

6.1 Задание

Типичное задание для самостоятельной работы состоит в следующем. По заданному варианту экспериментальных данных следует:

1. Составить вариационный ряд для статистической обработки результатов наблюдений.

2. Для полученного вариационного ряда определить следующие точечные оценки параметров распределения:

(a) Меры центральной тенденции.

(b) Абсолютные и средние показатели вариации данных.

(c) Показатели относительного рассеивания.

3. Построить доверительные интервалы для математического ожидания и дисперсии генеральной совокупности с надежностью р = 0.95.

4. Построить полигон, гистограмму (эмпирическую плотность распределения) и кумуляту (эмпирическую функцию распределения).

5. Проверить гипотезу о том, что случайная величина распределена по нормальному закону, используя точечные оценки.

6. Проверить гипотезу о том, что случайная величина распределена по нормальному закону, используя критерий согласия ² Пирсона при уровне значимости α = 0.05. Построить на одном чертеже гистограмму и соответствующую нормальную кривую. Построить на одном чертеже кумуляту и соответствующую теоретическую кривую.

Выборочные данные приведены в табл. 2, объем выборки 30.

Таблица 2 - Выборочные данные

25 26 23 15 14 42 33 23 36 47 31 27 25 33 23 23 33 26 19 24 26 43 41 12 16 18 29 32 39 31

6.2 Решение

Для данной выборки построим вариационный ряд x_i, i = 1, …, n, для чего выборочные значения расположим в порядке возрастания. Получим вариационный ряд, представленный в табл.3.

Таблица 6.1 - Вариационный ряд

12 14 15 16 18 19 23 23 23 23 24 25 25 26 26 26 27 29 31 31 32 33 33 33 36 39 41 42 43 47

Вычисление точечных оценок

Для вычисления мер центральной тенденции и показателей вариации данных составим вспомогательную табл. 4.

В результате получаем точечные оценки.

1. Выборочная средняя арифметическая, формула (2.1),

Таблица 6.2 – Таблица для расчета точечных оценок

i	xi	xi2	xi - Ẋ	ǀxi - Ẋǀ	(xi - Ẋ)2	(xi - Ẋ)3	(xi - Ẋ)4
1	12	144	-15,8333	15,83333	250,6944	-3969,33	62847,7
2	14	196	-13,8333	13,83333	191,3611	-2647,16	36619,07
3	15	225	-12,8333	12,83333	164,6944	-2113,58	27124,26
4	16	256	-11,8333	11,83333	140,0278	-1657	19607,78
5	18	324	-9,83333	9,833333	96,69444	-950,829	9349,816
6	19	361	-8,83333	8,833333	78,02778	-689,245	6088,334
7	23	529	-4,83333	4,833333	23,36111	-112,912	545,7415
8	23	529	-4,83333	4,833333	23,36111	-112,912	545,7415
9	23	529	-4,83333	4,833333	23,36111	-112,912	545,7415
10	23	529	-4,83333	4,833333	23,36111	-112,912	545,7415
11	24	576	-3,83333	3,833333	14,69444	-56,3287	215,9267
12	25	625	-2,83333	2,833333	8,027778	-22,7454	64,44522
13	25	625	-2,83333	2,833333	8,027778	-22,7454	64,44522
14	26	676	-1,83333	1,833333	3,361111	-6,16204	11,29707
15	26	676	-1,83333	1,833333	3,361111	-6,16204	11,29707
16	26	676	-1,83333	1,833333	3,361111	-6,16204	11,29707
17	27	729	-0,83333	0,833333	0,694444	-0,5787	0,482253
18	29	841	1,166667	1,166667	1,361111	1,587963	1,852623
19	31	961	3,166667	3,166667	10,02778	31,75463	100,5563
20	31	961	3,166667	3,166667	10,02778	31,75463	100,5563
21	32	1024	4,166667	4,166667	17,36111	72,33796	301,4082
22	33	1089	5,166667	5,166667	26,69444	137,9213	712,5934
23	33	1089	5,166667	5,166667	26,69444	137,9213	712,5934
24	33	1089	5,166667	5,166667	26,69444	137,9213	712,5934
25	36	1296	8,166667	8,166667	66,69444	544,6713	4448,149
26	39	1521	11,16667	11,16667	124,6944	1392,421	15548,7
27	41	1681	13,16667	13,16667	173,3611	2282,588	30054,07
28	42	1764	14,16667	14,16667	200,6944	2843,171	40278,26
29	43	1849	15,16667	15,16667	230,0278	3488,755	52912,78
30	47	2209	19,16667	19,16667	367,3611	7041,088	134954,2

2. Выборочная медиана, формула (2.3). Так как n – четное, то оценка медианы:

3. Выборочная мода, формула (2.4). Отсюда оценка моды:

Абсолютные и средние показатели вариации данных

1. Размах вариации, формула (2.5),

2. Среднее линейное отклонение, формула (2.6),

3. Выборочная дисперсия, формула (2.7), и исправленная выборочная дисперсия, формула (2.8):

,

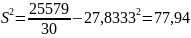Соответствующие выборочные средние квадратичные отклонения

Ошибка выборочного среднего, формула (2.11),

Показатели относительного рассеивания

1. Коэффициент вариации и исправленный коэффициент вариации, формула (2.12):

,

2. Относительное линейное отклонение, формула (2.13):

3. Коэффициент осцилляции, формула (2.14):

Показатели асимметрии и эксцесса

Для вычисления моментов и показателей асимметрии и эксцесса используем таблицу 6.2. В результате получим:

1. Точечные оценки асимметрии и ошибки оценок, формулы (2.15,2.16),

А = 0,27; S_A = 0,41; Ẩ = 0,28; S_Ẩ = 0,42.

2. Точечные оценки эксцесса и ошибки оценок, формулы (2.17, 2.18),

E = - 0,57; S_E = 0,75; Ẽ = 5,32; S_Ẽ = 0,83.

Вычисление интервальных оценок

1. При р = 0,95 и υ = n - 1 = 29 находим (см. ПРИЛОЛЖЕНИЕ, табл.1):

Отсюда доверительный интервал для математического ожидания, формула (3.2),

2. При р = 0,95 и υ = n - 1 = 29 находим (см. ПРИЛОЛЖЕНИЕ, табл.2):

Отсюда доверительный интервал для дисперсии, формула (3.4),

Доверительный интервал для среднеквадратичного отклонения

,

Эмперическая плотность распределения, полигон, гистрограмма

Превратим данные в интервальный вариационный ряд. Для этого разобьем весь диапазон наблюдаемых значений на k интервалов (классов). Число классов определим по правилу Штюргеса:

Число классов рекомендуется выбирать нечетным. Имеем

,

отсюда k = 5. По исходным данным находим минимальное и максимальное выборочные значения:

Длину частичных интервалов определим по формуле:

.

Границы интервалов ξ_i, i = 0, …, k определяются соотношением

Таблица 6.3 – Интервальный вариационный ряд

[ξi, ξi+1]	[12, 19)	[19, 26)	[26, 33)	[33, 40)	[40, 47]
xin	15,5	22,5	29,5	36,5	43,5
ni	5	8	8	5	4

Подсчитаем частоты n_i попадания наблюдаемых значений случайной величины в частотные интервалы. Все значения признака в пределах интервала приравняем его срединному значению, формула (4.1). Получим интервальный вариационный ряд, задаваемый таблицу 6.3.

Составим интервальный ряд распределения относительных и накопленных частот (таблица 6.4), в нашем случае h = 7.

Таблица 6.4 – Распределение частот

[ξi, ξi+1]	[12, 19)	[19, 26)	[26, 33)	[33, 40)	[40, 47]
xin	15,5	22,5	29,5	36,5	43,5
ωi=ni/n	0,1666667	0,2666667	0,266667	0,166667	0,13333333
ωi/h	0,0238095	0,0380952	0,038095	0,02381	0,01904762
ci	0,1666667	0,4333333	0,7	0,866667	1
ci/h	0,0238095	0,0619048	0,1	0,12381	0,14285714

Для построения полигона относительных частот (рисунок 6.1) на оси абсцисс откладываются варианты x_iⁿ, им соответствует значения ω_i на оси ординат, строится ломаная, соединяющая указанные точки. Для построения гистограммы (рисунок 6.1) на оси абсцисс откладываем частичные интервалы, на каждом из которых строим прямоугольник, высота которого равна ω_i/h.

Рисунок 6.1 – Полигон относительных частот (а) и гистограмма (b)

Эмпирическая функция распределения и кумулята

Аналитическая формула для эмперической функции распределения определяется множеством c_i и имеет вид, формула (4.3):

График эмперической функции распределения представлен на рисунке 6.2. Для построения кумулятора на оси абсцисс откладываются варианты x_i^*, им соответствует значения c_i на оси ординат, строится ломаная, соединяющая указанные точки. Кумулята изоражена на рисунке 2.

Рисунок 6.2 – Эмперическая функция распределения для интервального ряда (а); кумулята эмперического распределения для интервального ряда (b).

Проверка гипотезы нормального распределения по оценке среднего линейного отклонения

Для исходных данных проверяем неравенство, формула (5.1):

Так как неравенство выполняется, гипотеза нормальности может быть принята

Прверка гипотезы нормального распределения по оценкам ассиметрии и эксцесса

Имеем, формула (5.2),

.

В данном случае гипотеза нормальности исследуемого распределения может быть принята.

Проверка гипотезы нормального распределения по критерию согласия Пирсона (критерий χ²)

Рассмотрим критерии χ². Вид полигона и гистограммы частостей напоминает нормальную кривую (кривую Гаусса). Составим таблицу 6.5 для расчетов по формулам (5.4-5.5).

Таблица 6.5 – Расчет нормализованных границ

i	ξi	ξi+1	ξi - Ẋ	ξi+1 - Ẋ	zi	zi+1
1	12	19	-15,8333	-8,8333	-∞	-1,000374
2	19	26	-8,8333	-1,8333	-1,0003737	-0,207622
3	26	33	-1,8333	5,1667	-0,2076217	0,5851302
4	33	40	5,1667	12,1667	0,58513024	1,3778822
5	40	47	12,1667	19,1667	1,37788222	+∞

Вычислим теоретические частоты (5.6). Для этого составим расчетную таблицу 6.6.

Таблица 6.6 – Расчет теоретических частот

i	Ф(zi)	Ф(zi+1)	Pi = Ф(zi+1) - Ф(zi)	n’I = nPi
1	-0,5	0,341	0,159	4,77
2	0,341	0,0815	0,2595	7,785
3	0,0815	0,221	0,3025	9,075
4	0,221	0,413	0,192	5,76
5	0,413	0,5	0,087	2,61

Вычислим наблюдаемое значение критерия Пирсона (5.8). Для этого составим расчетную таблицу 6.7.

Таблицу 6.7 – Расчет значения χ²_набл

i
1	5	4,77	0,23	0,0529	0,01109015
2	8	7,785	0,215	0,046225	0,0059377
3	8	9,075	-1,075	1,155625	0,1273416
4	5	5,76	-0,76	0,5776	0,10027778
5	4	2,61	1,39	1,9321	0,7402682
∑	30	30

Сумма теоретических частот (контроль)

Наблюдаемое значение критерия Пирсона

По таблице критических точек распределения χ² (см. ПРИЛОЖЕНИЕ табл.2), по уровню значимости α = 0,05 и числу степеней свободы k – 3 = 2 находим критическую точку правосторонней критической области (5.9):

Так как – принимаем гипотезу о нормальном распределении генеральной совокупности Х.

Графическая иллюстрация

Плотность вероятности нормального распределения имеет вид

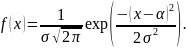
Функция распределения предполагаемого нормального распределения имеет вид:

Точечные оценки параметров α и σ были найдены:

Для построения графиков протабулируем функции f(x) и F(x) (см.ПРИЛОЖЕНИЕ, табл.3,4). Составим вспомогательную таблицу 6.8.

Таблица 6.8 – Таблица для построения графиков

i	x							f(x)
1
2
3
4
5
6
7
8

Гистограмма и нормальная кривая f(x) с параметрами Ẋ и Ṡ изображены на рисунке 6.3. Максимальное значение кривой Гаусса равно 0,04. Кумулята и теоретическая кривая F(x) с параметрами Ẋ и Ṡ изображены на рисунке 6.3.

Рисунок 6.3 – Гистограмма эмпирического распределения и соответствующая нормальная кривая (а); кумулята эмпирического распределения и соответствующая теоретическая кривая (b).