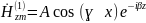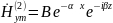Задача №2

Определить структуру гармонического электромагнитного поля в плоском диэлектрическом волноводе (световоде), изображённом на рис.3. Известны комплексные амплитуды двух проекций векторов поля в средах 1 и 2 при х≥0 (таблица 4). Параметры световода приведены в таблице 5.
Потери в диэлектриках сред отсутствуют.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧИ №2
Для решения задачи следует проработать раздел 10.7 в [1]. Алгоритм решения задачи рекомендуется следующим.
Определяются комплексные амплитуды всех остальных проекций у векторов и в средах 1 и 2 при х≥0.
Составляются и совместно решаются уравнения, которые связывают между собой неизвестные поперечные волновые числа в средах 1 и 2, т.е. и
 .
.Определяются минимальная и максимальная толщины световода, при которых по нему будет распространяться только волна низшего типа.
Для средней толщины световода вычисляются параметры для волны низшего типа, т.е. , ,β и
 .
.Используя заданную величину единичной мощности волны либо в среде 1, либо в среде 2, т.е.
 и
и
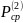 ,
определяют амплитуды А и В, входящие в
выражения для всех проекций векторов
и
.
,
определяют амплитуды А и В, входящие в
выражения для всех проекций векторов
и
.Строятся зависимости амплитуд всех проекций векторов и от координаты х в области х≥0.
Учитывая симметрию световода относительно оси z, характер построенных зависимостей следует распространить на область х≤0.
Изображается структура линий векторов для волны низшего типа в сечении x0z.
Таблица 4
Последняя цифра номера студ. билета |
Известные проекции векторов в среде 1 |
Известные проекции векторов в среде 2 |
Дополнительные сведения |
0 |
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
Таблица 5
-
Параметр
Предпоследняя цифра студенческого билета
9
8
7
6
5
4
3
2
1
0

2,3
2,25
2,6
2,5
2,9
2,5
2,4
2,8
2,4
3

1,1
1
1,3
1,2
1,4
1,2
1,1
1,4
1,2
1,5
λ,мкм
1,3
1,6
1,3
1,3
1,3
1,55
1,5
1,55
1,55
1,2

–
–
1
2
–
–
1,5
–
3,5
1,2

1,5
1
–
–
0,5
2
–
3
–
–
Поясним решение основных пунктов задания.
Для выполнения пункта 1 надо записать уравнения Максвелла для гармонического поля и использовать далее следующее представление:
rot =
=
В результате два векторных уравнения преобразуются в шесть скалярных уравнений. Упростив их после подстановки вида

следует их решить.
Для выполнения пункта 2 следует записать граничные условия вида:


В этих соотношениях надо положить х=h. В результате получается два алгебраических уравнения, в которые входят неизвестные величины , и А,В. Исключив из этих уравнений величины А и В, получаем одно уравнение, в которое входят только неизвестные величины , . Это уравнение далее следует преобразовать, например, в такое:

Решение этого уравнения, которое является трансцендентным, в графической форме представлено на рис. 4 в виде двух сплошных кривых. Пунктиром изображены четверти окружностей, которые представляют собой уравнения следующего вида:

где,
k=ω –волновое
число в вакууме.
–волновое
число в вакууме.
Наличие
двух точек пересечения для верхней
четверти окружности с двумя сплошными
кривыми говорит о том, что в световоде
распространяются два типа волны. Если,
например, по заданию
 и
и
 ,
то это будут волны
,
то это будут волны
 (точка
1) и
(точка
1) и
 (точка
2). Низшим типом является волна
.
Точка 3 соответствует максимальной
толщине световода, точка 0–минимальной
(нулевой) толщине световода. Точка 4
соответствует средней толщине световода.
(точка
2). Низшим типом является волна
.
Точка 3 соответствует максимальной
толщине световода, точка 0–минимальной
(нулевой) толщине световода. Точка 4
соответствует средней толщине световода.
Фазовая скорость волны определяется по формуле:
где
коэффициент фазы
 вычисляется из любого соотношения,
приведённого ниже:
вычисляется из любого соотношения,
приведённого ниже:


Д
*
ля вычисления амплитуд А и В следует использовать значения единичных мощностей в таблице 5 и выражения для проекций векторов:



л
*
ибо