ФЕДЕРАЛЬНОЕ АГЕНСТВО СВЯЗИ

Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования

Московский технический университет связи и информатики

Кафедра технической электродинамики и антенн

Методические указания и задания к контрольной и курсовой работам по курсу:

ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ И ВОЛНЫ

для студентов-заочников 2 и 3 курсов

(направление 11.03.02)

Москва 2016

План УМД на 2017/2018 уч.г.

Методические указания и задания к контрольной и курсовой работам по курсу:

ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ И ВОЛНЫ

Составители: В.М. Седов, к.т.н., доцент

В.И. Корнюхин, к.т.н., доцент

Рецензент:Т.Н. Федотова, старший преподаватель

Издание утверждено на заседании кафедры.

Протокол заседания кафедры № от . . г

Общие замечания

Курс «Электромагнитные поля и волны» состоит из двух частей. В первой части курса изучается общая теория электромагнитных волн, которая базируется на уравнениях Максвелла. С волнами такой природы приходится сталкиваться при работе многих устройств связи, как-то: электрических и оптических кабелей, антенно-фидерных устройств, трактов радиорелейных, спутниковых и оптических систем передачи и т.д. Во второй части курсаизучаются параметры и структуры электромагнитных волн в различных типах линий передачи, как-то: коаксиальной линии, прямоугольном и круглом волноводах, диэлектрическом волноводе и т.д.

Для успешного усвоения курса студент обязан владеть основами векторного анализа, методами решения однородных уравнений второго порядка в частных производных, а также обладать общими представлениями о гармонических колебаниях и волнах.

Первая часть курса студентами изучается в 4 семестре. В этом семестре студент выполняет контрольную работу и сдает зачёт.

Вторая часть курса студентами изучается в 5 семестре. В этом семестре студент выполняет курсовую работу, проходит лабораторный практикум и сдаёт экзамен. Защита курсовой работы с оценкой производится перед экзаменом.

Курсовая работа включает в себя четыре задачи. Студенты, обучающиеся по профилям 5 и 7, решают задачи №3 и №4.

Профиль №3–Многоканальные телекоммуникационные системы,

Профиль №4–Сети связи и системы коммутации,

Профиль №5– Системы мобильной связи,

Профиль №7– Системы радиосвязи и радиодоступа.

В заключение укажем, что в первую часть входят 1–5 разделы курса, во вторую часть-соответственно 6–11 разделы курса.

Список литературы

Основания

1. Пименов Ю.В., Вольман В.И., Муравцов А.Д. Техническая электродинамика. –М.:Радио и связь, 2000–536с.

2. Вольман В.И., Пименов Ю.В., Техническая электродинамика. –М.:Связь, 1971. –487с.

Дополнительная

3. Седов В.М., Гайнутдинов Т.А. Электромагнитные поля и волны (конспект лекций)/МТУСИ. –М., 2000. –49с.

4. Ерохин Г.А, Седов В.М. Задания на курсовую работу и методические указания по её выполнению для дистанционной формы обучения/МТУСИ. –М., 2000. – 14с.

Методические указания к изучению разделов программы курса.

1. Общие закономерности электромагнитных полей.

[1, гл.1, разд. 2, 3], [3, §1 – 7].

Изучаемые вопросы

1. Векторы электромагнитного поля и параметры среды.

2. Закон Ома в дифференциальной форме.

3. Уравнения Максвелла в интегральной форме. Ток смещения.

4. Уравнения Максвелла в дифференциальной форме.

5. Закон сохранения заряда. Уравнение непрерывности полного тока.

6. Граничные условия.

7. Энергия электромагнитного поля. Теорема Пойнтинга.

2. Монохроматическое электромагнитное поле

[1, разд.2.3. 2, 2.4.2], [4,стр.5].

Изучаемые вопросы

1. Уравнения Максвелла для гармонического поля.

2. Комплексная диэлектрическая проницаемость среды.

3. Волновые уравнения для комплексных амплитуд полей.

4. Электродинамические потенциалы.

3. Излучатели электромагнитных волн

[1, гл.5], [3, §9].

Изучаемые вопросы

1. Элементарный электрический излучатель:

а) физическая модель,

б) методика определения поля,

в) анализ структуры поля в ближней и дальней зонах,

г) мощность и сопротивление излучения,

д) диаграмма направленности.

2. Элементарный магнитный излучатель:

а) физическая модель,

б) структура поля в дальней зоне,

в) диаграмма направленности.

3. Элемент Гайгенса:

а) физический смысл,

б) определение направленных свойств.

4. Плоские электромагнитные волны в однородной изотропной среде.

[1, гл.6], 3, §8].

Изучаемые вопросы

1. Плоская волна как решение волнового уравнения Гельмгольца.

2. Основные параметры плоской волны.

3. Зависимость параметров волны от частоты.

4. Плоская волна в диэлектрике.

5. Плоская волна в среде с потерями.

6. Поляризация волны.

5. Волновые явления на границе раздела сред.

[1, гл.7], 3, §10].

Изучаемые вопросы

1. Структура полей при падении плоской волны на границу раздела двух сред.

2. Законы Снеллиуса. Формулы Френеля.

3. Полное прохождение волны во вторую среду.

4. Явление полного внутреннего отражения.

6. Общие свойства электромагнитных волн в линиях передачи.

[1, гл.9], [3, §11].

Изучаемые вопросы

1. Понятие линии передачи. Типы регулярных линий передачи.

2. Связь между поперечными и продольными проекциями у векторов полей.

3. Классификация направляемых волн.

4. Основные свойства направляемых волн: критическая частота, фазовая скорость, длина волны, скорость распространения энергии, ослабление, дисперсия.

5. Методика расчёта поля в регулярной линии передачи.

7. Т-волны в линиях передачи.

[1, разд. 10.4-10.6],[ 3, §14].

Изучаемые вопросы

1. Структура поля в двухпроводной линии передачи.

2. Структура поля в коаксиальной линии передачи.

3. Структура поля в полосковой линии передачи.

4. Одноволновый режим работы.

5. Основные параметры волн.

8. Н– и Е – волны в линиях передачи.

[1, разд. 10.1-10.2­­], [ 3, §12].

Изучаемые вопросы.

1. Структура полей в прямоугольном волноводе.

2. Структура полей в круглом волноводе.

3. Основная волна в этих волноводах.

4. Выбор поперечных размеров волноводов.

5. Токи на стенках волноводов.

6. Ослабление волн в волноводах.

9. Волны в круглом диэлектрическом волноводе.

[1, разд. 10.7.5, 10.7.6], [ 3, §13].

Изучаемые вопросы

1. Методика определения типов волн в волноводе.

2. Анализ дисперсионного уравнения.

3. Одноволновой режим работы волновода.

4. Параметры основной волны.

5. Использование диэлектрического волновода для построения оптических кабелей связи.

10. Линии передачи конечной длины.

[1, разд. 12.1.2 –12.1.4, 12.2.1 – 12.2.4].

Изучаемые вопросы

1. Характер распределения токов и напряжений для различных нагрузок.

2. Коэффициенты бегущей и стоячей волн.

3. Эквивалентное сопротивление линии.

4. Круговая диаграмма сопротивлений.

5. Способы согласования линии с нагрузкой.

11. Объёмные резонаторы

[1, гл.11].

Изучаемые вопросы

1. Основные параметры: резонансная частота, добротность.

2. Потери энергии в резонаторе. Собственная, внешняя и нагруженная добротности.

3. Резонаторы в виде отрезков регулярных линий передачи.

4. Квазистационарные резонаторы.

5. Резонаторы оптического диапазона.

Задание на контрольную работу

В полупространстве х>0, ограниченном снизу идеально –проводящей плоскостью S (рис.1), распространяется гармоническая электромагнитная волна. Известны некоторые проекции векторов либо сами векторы поля у этой волны. Они указаны в таблице 1 в соответствии с последней цифрой номера студенческого билета. Параметры среды в полупространстве х>0 и ряд других параметров поля волны приведены в таблице 2 по предпоследней цифре номера студенческого билета.

Требуется:

1. определить неизвестные проекции либо сами векторы заданного поля волны и охарактеризовать тип волны;

2. проверить выполнение граничных условий на плоскости(поверхности) S;

3. записать выражения для мгновенных значений всех проекций поля волны;

4. записать выражения для мгновенного, комплексного и среднего за период значения вектора Пойнтинга;

Таблица 1

Последняя цифра номера студенческого билета	Проекция векторов либо сами векторы электромагнитного поля.
0	= ,
1	, ,
2	,
3
4
5
6	,
7	, ,
8
9	,

Таблица 2

предпоследняя цифра номера студенческого билета	f, МГц	,	,				ϭ,
0	550	22	40	1	1	0,9	34
1	600	35	18	2,5	1	0,4	45
2	150	17	60	1	1	0,8	66
3	400	25	30	1,8	1	0,3	34
4	550	20	40	2,3	1	0,7	58
5	250	30	20	1,2	1	0,6	34
6	500	40	15	1,4	1	0,4	66
7	300	16	30	1	1	0,8	45
8	350	10	50	1,7	1	0,5	34
9	400	35	25	1,5	1	0,3	58

5. определить комплексную амплитуду плотности тока, протекающего по поверхности(плоскости) S;

6. рассчитать фазовый коэффициент волны;

7. рассчитать фазовую скорость волны, скорость распространения энергии волны, длину волны;

8. построить зависимости ненулевых мгновенных значений проекции полей волны от координаты х в сечении для момента времени , где Т-период высокой частоты;

9. определить потери мощности волны, приходящиеся на единичную площадку поверхности S, если в качестве этой поверхности использовать реальный проводник с удельной проводимостью .

Методические указания к решению контрольной работы.

Решать пункт 1 задания следует одним из двух возможных способов.

Первый способ используется, когда в таблице №1 заданы все три проекции либо вектора , либо вектора . В этом случае надо воспользоваться только одним уравнением Максвелла (1.76) в [1]. Пусть, например, заданы три проекции вектора :

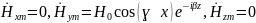
Для определения неизвестных проекций вектора используем верхнее уравнение:

rot = (1)

В этом уравнении, как видим, используется обозначение (1.61) в [1]:

В полупространстве х>0 удельная проводимость и поэтому

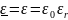, где

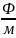, –электрическая постоянная,

–относительная диэлектрическая проницаемость среды в полупространстве х>0(задана в таблице № 2)

Раскрывая определитель в (1), получаем:

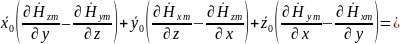
Приравняв в левой и правой частях этого соотношения одноимённые проекции, получаем:

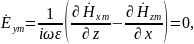
Если в таблице №1 заданы три проекции вектора , то поступаем аналогично, т.е. используем нижнее уравнение Максвелла(1.76) в [1]. В этом уравнении надо положить:

, где

x>0(задана в таблице №2).

Второй способ используется в том случае, когда в таблице №1 заданы продольные проекции и вектора , и вектора . В этом случае для определения неизвестных поперечных проекций векторов , , и 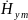необходимо совместно решать оба уравнения Максвелла (1.76) в [1].Результатом такого решения является соотношение (9.5) в [1]. Их и надо использовать для решения.

В заключение решения пункта 1(независимо от способа решения) следует выписать все проекции заданного электромагнитного поля. Для рассмотренного выше примера они будут иметь следующий вид:

,

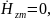
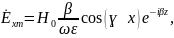(2)

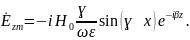
Вывод: заданное электромагнитное поле представляет собой плоскую неоднородную гармоническую волну электрического типа.

Решение пункта 2 заключается в доказательстве того, что на поверхности S(рис.1), имеющей бесконечную проводимость, отсутствуют нормальная проекция у вектора и касательная проекция у вектора . С этой целью надо в соотношениях (2) принять х=0

Чтобы решить пункт 3 следует учесть, что согласно методу комплексных амплитуд, для перехода от комплексной амплитуды к мгновенному значению амплитуды А(t) следует произвести следующую математическую операцию:

А(t)=Re( ).

В результате получаем мгновенные значения для всех проекций векторов заданного поля:

Для данного частного случая имеем:

.

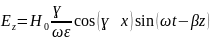Д

*

ля решения пункта 4 надо, воспользоваться соотношениями вида:

=[ ;

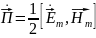(4)

.

П

*

роекции векторов, указанных в (4), следует взять из соотношений (2) и (3). Если рассмотреть всё тот же частный случай, то имеем:

,

.

Для решения пункта 5 надо использовать следующее векторное соотношение:

где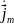 –комплексная амплитуда плотности тока на поверхности S,

= единичный орт внешней нормали к этой поверхности,

–комплексная амплитуда напряженности магнитного поля на этой поверхности.

Для данного частного случаяимеем:

.

При решении пункта 6 следует использовать соотношение (9.11) в [1]:

где –поперечное волновое число,

K=ω –волновое число для волны в свободном пространстве.

Расчеты по пункту 7 следует выполнять, используя соотношения:

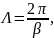
Для выполнения пункта 8 следует использовать выражения (3), полученные ранее при решении пункта 3. В эти выражения надо подставить все константы, а затем произвести расчёты функций при изменении координаты х в пределах 0≤х≤2 , где –длина «стоячей» волны:

При построении графиков для рассчитанных функций требуется, чтобы масштабы величин по осям были целыми числами. С этой целью необходимо использовать такие единицы измерения, как мА, µВ, см, мм и т.д.

Вычисление потерь волны в пункте 9 следует выполнять по формуле вида:

где –комплексная амплитуда напряжённости магнитного поля волны на поверхности S при условии, что эта поверхность имеет бесконечную проводимость(для рассматриваемого частного случая ), поверхностное сопротивление реального проводника,

Величина 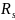вычисляется по формуле:

Рассчитанная по формуле (8) величина потерь должна быть выражена в мкВт.
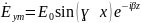
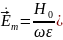
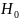