
- •Уравнения прямой на плоскости
- •1. Основные понятия.
- •2. Основные приложения метода координат на плоскости.
- •1) Расстояние между двумя точками
- •2) Деление отрезка в данном отношении
- •3. Линии на плоскости.
- •4. Уравнения прямой на плоскости.
- •1) Уравнение прямой с угловым коэффициентом.
- •2) Общее уравнение прямой.
- •Условия параллельности, перпендикулярности двух прямых
- •3) Уравнение прямой, проходящей через данную точку в данном направлении.
- •4) Уравнение прямой, проходящей через две точки.
- •5) Уравнение прямой в отрезках на осях.
- •6) Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
- •7) Каноническое уравнение прямой.
- •5. Прямая на плоскости. Основные задачи.
- •1) Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых
- •2) Расстояние от точки до прямой
7) Каноническое уравнение прямой.

Каноническим
уравнением прямой, проходящей через
данную точку 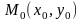 и
имеющей заданный направляющий вектор
и
имеющей заданный направляющий вектор 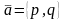 ,
называется уравнение вида
,
называется уравнение вида
 .
(13)
.
(13)
5. Прямая на плоскости. Основные задачи.
1) Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых
Пусть прямые
и
заданы уравнениями с угловыми
коэффициентами
 и
и
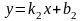 (см. рис. 16).
(см. рис. 16).
Т ребуется
найти угол
ребуется
найти угол
 ,
на который надо повернуть в положительном
направлении прямую
вокруг точки их пересечения до совпадения
с прямой
.
,
на который надо повернуть в положительном
направлении прямую
вокруг точки их пересечения до совпадения
с прямой
.
Решение:
Имеем
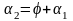 (теорема о внешнем угле треугольника)
или
(теорема о внешнем угле треугольника)
или
 .
.
Если
 , то
, то
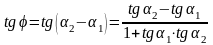 .
.
Рис.
16.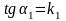 ,
,
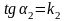 , поэтому
, поэтому
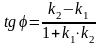 ,
(14)
,
(14)
откуда легко получим величину искомого угла.
Таким образом,
условием
перпендикулярности прямых является
равенство
 .
.
2) Расстояние от точки до прямой
Пусть заданы прямая
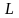 уравнением
и точка
(рис. 17). Требуется найти расстояние от
точки
уравнением
и точка
(рис. 17). Требуется найти расстояние от
точки
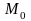 до прямой
.
до прямой
.
Решение:
Расстояние
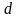 от точки
до прямой
равно модулю проекции вектора
от точки
до прямой
равно модулю проекции вектора
 ,
где
— произвольная точка прямой
,
на направление нормального вектора
.
Следовательно,
,
где
— произвольная точка прямой
,
на направление нормального вектора
.
Следовательно,
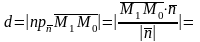
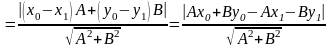 .
.
Так как точка
принадлежит прямой
,
то
 , т. е.
, т. е.
 . Поэтому
. Поэтому
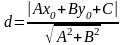 ,
(15)
,
(15)
что и требовалось получить.
Пример.
Найти расстояние от точки
 до прямой
до прямой

Решение: По формуле (14) получаем
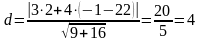 .
.

Рис. 17
