3) Уравнение прямой, проходящей через данную точку в данном направлении.

Пусть прямая проходит через точку М (х₀; у₀) и ее направление характеризуется угловым коэффициентом k. Уравнение этой прямой можно записать в виде , где b — пока неизвестная величина. Так как прямая проходит через точку М (х₀; у₀ ), то координаты точки удовлетворяют уравнению прямой: у₀ = kх₀ + b . Отсюда b = у₀ — kх₀ Подставляя значение b в уравнение у = kх + b , получим искомое уравнение прямой y = kx + y₀ – kx₀ , т. е.

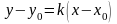. (7)

Уравнение (7) с различными значениями k называют также уравнениями пучка прямых с центром в точке . Из этого пучка нельзя определить лишь прямую, параллельную оси Оу.

4) Уравнение прямой, проходящей через две точки.

Пусть прямая проходит через точки и 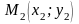. Уравнение прямой, прямой, проходящей через точку M₁, имеет вид

, (8)

где k — пока неизвестный коэффициент.

Так как прямая проходит через точку , то координаты этой точки должны удовлетворять уравнению (8): 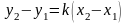.От­сюда находим . Подставляя найденное значение k в уравнение (8), получим уравнение прямой, проходящей через точки М₁ и М₂ :

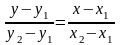. (9)

Предполагается, что в этом уравнени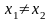и и .

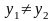Если 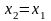, то прямая, проходящая через точки и параллельна оси ординат. Ее уравнение имеет вид .

Если 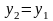, то уравнение прямой может быть записано в виде , прямая 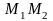параллельна оси абсцисс.

5) Уравнение прямой в отрезках на осях.

Пусть прямая пересекает ось Ох в точ­ке , а ось Оу — в точке (рис. 14). В этом случае уравнение (9) примет вид:

,

(10) .

Рис. 14

Это уравнение (10) называется уравнением прямой в отрезках, так как числа а и b указы­вают, какие отрезки отсекает прямая на осях координат.

6) Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

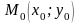Н айдем уравнение прямой, проходящей через заданную точку перпендикулярно данному ненулевому вектору 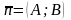. Возьмем на прямой произвольную точку ) и рассмотрим вектор 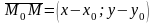(рис. 15).

Рис. 15

Поскольку векторы 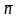и перпендикулярны , то их скалярное произведение равно нулю: 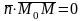, то есть

. (11)

Уравнение (11) называется уравнением прямой, про­ходящей через заданную точку перпендикулярно задан­ному вектору.

Как было отмечено выше, вектор , перпендикулярный прямой, на­зывается нормальным вектором этой прямой.

Уравнение (11) можно переписать в виде

, (12)

где А и В — координаты нормального вектора, С = – Ax₀ – By₀ — свободный член. Уравнение (12) есть общее уравнение прямой.