
- •Уравнения прямой на плоскости
- •1. Основные понятия.
- •2. Основные приложения метода координат на плоскости.
- •1) Расстояние между двумя точками
- •2) Деление отрезка в данном отношении
- •3. Линии на плоскости.
- •4. Уравнения прямой на плоскости.
- •1) Уравнение прямой с угловым коэффициентом.
- •2) Общее уравнение прямой.
- •Условия параллельности, перпендикулярности двух прямых
- •3) Уравнение прямой, проходящей через данную точку в данном направлении.
- •4) Уравнение прямой, проходящей через две точки.
- •5) Уравнение прямой в отрезках на осях.
- •6) Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
- •7) Каноническое уравнение прямой.
- •5. Прямая на плоскости. Основные задачи.
- •1) Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых
- •2) Расстояние от точки до прямой
2) Деление отрезка в данном отношении
Требуется разделить
отрезок АВ,
соединяющий точки
и
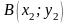 ,
в заданном отношении
,
в заданном отношении
 , т.е. найти координаты точки
, т.е. найти координаты точки
 отрезка АВ
такой, что
отрезка АВ
такой, что
 (рис. 3).
(рис. 3).

Для нахождения координат точки используют
формулы
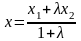 ;
;
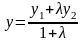 (2)
(2)
Рис. 3
Формулы (2) называются
формулами
деления отрезка в данном отношении.
В частности, при λ
= 1,
т. е. если AM
= MB,
то они примут вид
 ,
,
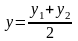 .
В этом случае точка М(х;у)
является серединой
отрезка АВ.
.
В этом случае точка М(х;у)
является серединой
отрезка АВ.
3. Линии на плоскости.
Линия на плоскости рассматривается (задается) как множество точек, обладающих некоторым только им присущим геометрическим свойством. Например, окружность радиуса R есть множество всех точек плоскости, удаленных на расстояние R от некоторой фиксированной точки О (центра окружности).
Уравнением линии (или кривой) на плоскости Оху называется такое уравнение F(x;y) = 0 с двумя переменными, которому удовлетворяют координаты х и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Переменные х и у в уравнении линии называются текущими координатами точек линии.
Уравнение линии позволяет изучение геометрических свойств линии заменить исследованием его уравнения.
Так, для того чтобы установить, лежит ли точка А(хо ;уо) на данной линии, достаточно проверить (не прибегая к геометрическим построениям), удовлетворяют ли координаты точки А уравнению этой линии в выбранной системе координат.
Задача о нахождении точек пересечения двух линий, заданных уравнениями F1(x;y) = 0 и F2(x;y) = 0, сводится к отысканию точек, координаты которых удовлетворяют уравнениям обеих линий, т. е. сводится к решению системы двух уравнений с двумя неизвестными:
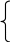
F1 ( x; y ) = 0,
F2 ( x; y ) = 0.
Если эта система не имеет действительных решений, то линии не пересекаются.
Аналогичным образом вводится понятие уравнения линии в полярной системе координат.
Уравнение F ( r; φ ) = 0 называется уравнением данной линии в полярной системе координат, если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению.
 Линию
на плоскости можно задать при помощи
двух уравнений:
Линию
на плоскости можно задать при помощи
двух уравнений:
x = x ( t ) ,
y = y ( t ) , (3)
где х и у — координаты произвольной точки М (х; у ), лежащей на данной линии, a t — переменная, называемая параметром; параметр t определяет положение точки ( x; у ) на плоскости.
Например, если x = t + 1 , y = t2 , то значению параметра t = 2 соответствует на плоскости точка (3; 4), т. к. х = 2 + 1 = 3, у = 22 = 4.
Если параметр t изменяется, то точка на плоскости перемещается, описывая данную линию. Такой способ задания линии называется паpaметрическим, а уравнения (3) — параметрическими уравнениями линии.
В аналитической геометрии на плоскости возникают две основные задачи. Первая: зная геометрические свойства кривой, найти ее уравнение; вторая: зная уравнение кривой, изучить ее форму и свойства.
 На
рисунках 4-12 приведены примеры некоторых
кривых и указаны их уравнения.
На
рисунках 4-12 приведены примеры некоторых
кривых и указаны их уравнения.
|
или |
|
|
Рис. 4. Окружность радиуса R |
|||
|
|
|
||
Рис. 5. Лемниската Бернулли Уравнение в прямоугольных координатах:
в полярных координатах:
|
Рис. 6. Трилепестковая роза В полярных координатах ее уравнение имеет вид:
|
|
||
|
|
|
||
Рис. 7. Улитка Паскаля Уравнение
в полярных координатах имеет вид :
|
||||
|
|
Рис. 8. Полукубическая парабола
Уравнение кривой
|
Рис. 9. Астроида
Уравнение в прямоугольных координатах:
параметрические уравнения:
|
|
|
Рис. 10. Кардиоида Уравнение
в полярных координатах имеет вид
|
Рис. 11. Спираль Архимеда
Уравнение кривой
в полярных координатах
|
|
Рис. 12. Циклоида Параметрические уравнения циклоиды имеют вид
где а > 0. Циклоида — это кривая, которую описывает фиксированная точка окружности, катящаяся без скольжения по неподвижной прямой. |




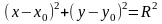


 ,
,
 ;
;
 .
. , где a
> 0 .
, где a
> 0 .


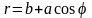 .
.

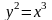 или
или
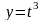 .
.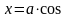


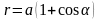 , где а
> 0. Кардиоида — частный случай
улитки Паскаля (
а = b
).
, где а
> 0. Кардиоида — частный случай
улитки Паскаля (
а = b
).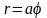 , где а >
0 —
постоянное.
, где а >
0 —
постоянное.
