
4 Лабораторная работа / 4-Лабораторная работа (Физика)_4 / Отчет по ЛР №4
.doc
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра физики
ОТЧЕТ
Лабораторная работа по курсу "Общая физика"
ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ КРУГОВОГО ТОКА
Преподаватель Студент группы ХХХ
___________ /________/ / ________ /
___________2004 г. _______________ 2004 г.
Томск 2004
1. ЦЕЛЬ РАБОТЫ
Целью данной работы является изучение магнитного поля на оси витка с током и экспериментальная проверка закона Био‑Савара‑Лапласа.
2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА
Э кспериментальная
установка, схематично представленная
на рис.2.1., состоит из катушки 1 с током,
создающей магнитное поле, измерительной
катушки 2 и осциллографа 3. Катушка 1
питается через понижающий трансформатор
переменным током. Все устройство
смонтировано на лабораторном макете.
Измерительная катушка 2 расположена
под лицевой панелью макета и может
перемещаться вдоль оси катушки 1 с
помощью движка.
кспериментальная
установка, схематично представленная
на рис.2.1., состоит из катушки 1 с током,
создающей магнитное поле, измерительной
катушки 2 и осциллографа 3. Катушка 1
питается через понижающий трансформатор
переменным током. Все устройство
смонтировано на лабораторном макете.
Измерительная катушка 2 расположена
под лицевой панелью макета и может
перемещаться вдоль оси катушки 1 с
помощью движка.
3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Выражение для расчета амплитудного значения магнитной индукции в любой точке на оси z катушки:
Bm = Em / N1 S , (3.1)
где Em - амплитудное значение ЭДС катушки, измеренное с помощью осциллографа;
S - площадь поперечного сечения измерительной катушки (в данной работе S = 310-4 м2);
= 2 , где - частота переменного напряжения, питающего круговой виток ( = 50 Гц);
N1= 3020 - число витков измерительной катушки.
Относительная погрешность косвенного измерения циклической частоты переменного тока:
![]() , (3.2)
, (3.2)
где ε(π) = 0,005/3,14 = 0,0016 (1,6%) и ε(ν) – относительные погрешности измерения числа π и частоты переменного напряжения, питающего круговой виток.
Относительная погрешность косвенного измерения величины амплитудного значения магнитной индукции в любой точке на оси z катушки:
![]() , (3.3),
, (3.3),
где ε(Em), ε(N1) и ε(S) – относительные погрешности измерения амплитудного значения э.д.с., числа витков и площади поперечного сечения измерительной катушки.
Абсолютная погрешность косвенного измерения величины амплитудного значения магнитной индукции в любой точке на оси z катушки:
σ(Bm) = ε(Bm)·Bm/100 (3.4)
Абсолютная погрешность измерения величины амплитудного значения э.д.с. Em:
σ(Em) = ε(Em)·Em/100 (3.5)
Относительная погрешность косвенного измерения величины (Em)-2/3:
ε((Em)-2/3) = 2/3·ε(Em) (3.6)
Абсолютная погрешность косвенного измерения величины (Em)-2/3:
σ((Em)-2/3) = ε((Em)-2/3)·(Em)-2/3/100 = 2/3·ε(Em)·Em-2/3/100 (3.7)
Абсолютная погрешность косвенного измерения квадрата расстояния по оси витка от его центра z2:
σ(z2) = 2·z·σ(z), (3.8),
где σ(z) – абсолютная погрешность прямого измерения величины z.
4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ
Экспериментальные данные и результаты их обработки представлены в таблице 4.1.
N=4840
Таблица 4.1
Результаты прямых и косвенных измерений
|
z , м |
Em , В |
(Em)-2/3, В-2/3 |
z2 , см2 |
Примечания |
|
0 |
1,350 |
0,8187 |
0,00 |
( Em) =10% (S) = 10% ( N1) = 1% () = 1% |
|
1 |
1,150 |
0,9110 |
1,00 |
|
|
2 |
0,800 |
1,1604 |
4,00 |
|
|
3 |
0,480 |
1,6312 |
9,00 |
|
|
4 |
0,300 |
2,2314 |
16,00 |
|
|
5 |
0,190 |
3,0257 |
25,00 |
|
|
6 |
0,120 |
4,1104 |
36,00 |
|
|
7 |
0,085 |
5,1727 |
49,00 |
|
|
8 |
0,060 |
6,5248 |
64,00 |
|
|
9 |
0,044 |
8,0235 |
81,00 |
Амплитудное значение индукции магнитного поля на оси катушки рассчитывалось по формуле (3.1).
С учетом доверительных интервалов, вычисленных по формулам (3.2) - (3.4), в точке, соответствующей центру витка оно получилось равным
Bm = 1,004 ± 0,0010 * 10-3 Тл
Относительная погрешность косвенного измерения циклической частоты переменного тока определяется по формуле 3.2
e(p) = 0,0016
e(v) = 0,0100
e(w) = 0,0101
Относительная погрешность косвенного измерения величины амплитудного значения магнитной индукции в любой точке на оси z катушки
|
Bm, Тл |
(Bm-<Bm>)2 |
|
0,00296 |
3,8249E-06 |
|
0,00252 |
2,3021E-06 |
|
0,00175 |
5,6247E-07 |
|
0,00105 |
2,3473E-09 |
|
0,00066 |
1,1983E-07 |
|
0,00042 |
3,4494E-07 |
|
0,00026 |
5,4874E-07 |
|
0,00019 |
6,6831E-07 |
|
0,00013 |
7,6092E-07 |
|
0,00010 |
8,2335E-07 |
|
0,00100 |
9,95793E-07 |
Таблица 4,2
Погрешности прямых и косвенных измерений
|
№ |
σ(z),м. |
σ(z2),м |
(Еm),В |
((Еm)-2/3), % |
σ((Еm)-2/3), В-2/3 |
|
1 |
0,001 |
0,0000 |
0,135 |
6,7 |
0,055 |
|
2 |
0,001 |
0,0020 |
0,115 |
6,7 |
0,061 |
|
3 |
0,001 |
0,0040 |
0,080 |
6,7 |
0,077 |
|
4 |
0,001 |
0,0060 |
0,048 |
6,7 |
0,109 |
|
5 |
0,001 |
0,0080 |
0,030 |
6,7 |
0,149 |
|
6 |
0,001 |
0,0100 |
0,019 |
6,7 |
0,202 |
|
7 |
0,001 |
0,0120 |
0,012 |
6,7 |
0,274 |
|
8 |
0,001 |
0,0140 |
0,009 |
6,7 |
0,345 |
|
9 |
0,001 |
0,0160 |
0,006 |
6,7 |
0,435 |
|
10 |
0,001 |
0,0180 |
0,004 |
6,7 |
0,535 |
Окончательные опытно-расчетные данные с учетом доверительных интервалов, полученных с применением правил округления, и необходимые для построения графиков приведены в таблице 4.3
Таблица 4.3
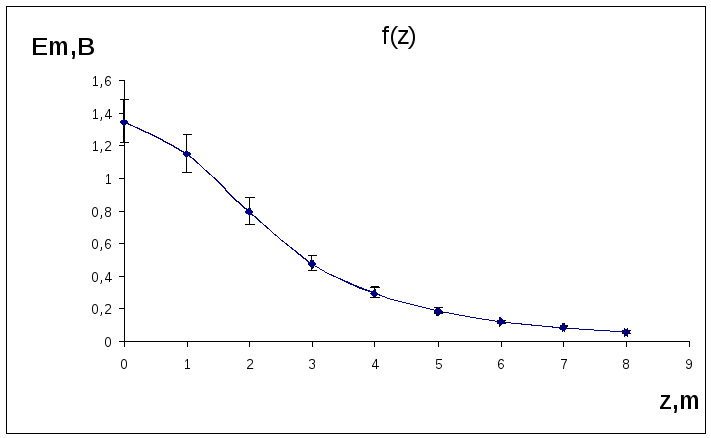
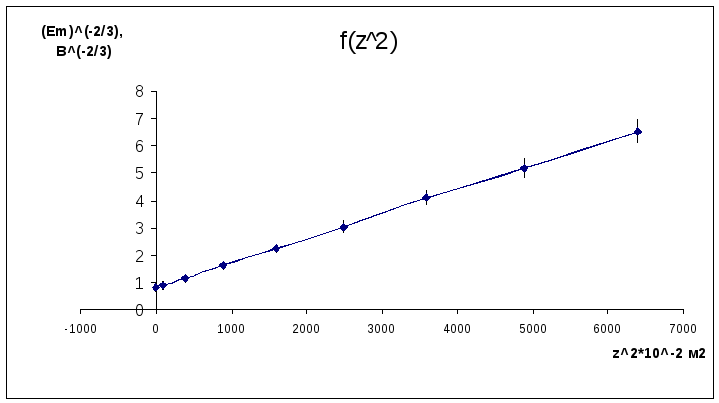
Опытно-расчетные данные для построения графиков зависимостей Em = f1(z) и (Em)-2/3 = f1(z2).
|
z, м |
Em,B |
Z2 *10-2,м2 |
(Еm)-2/3,B-2/3 |
|
0 |
1,350 ± 0,135 |
0,000 ± 0,000 |
0,8187 ± 0,055 |
|
1 |
1,150 ± 0,115 |
100,000 ± 0,200 |
0,9110 ± 0,061 |
|
2 |
0,800 ± 0,080 |
400,000 ± 0,400 |
1,1604 ± 0,077 |
|
3 |
0,480 ± 0,048 |
900,000 ± 0,600 |
1,6312 ± 0,109 |
|
4 |
0,300 ± 0,030 |
1600,000 ± 0,800 |
2,2314 ± 0,149 |
|
5 |
0,190 ± 0,019 |
2500,000 ± 1,000 |
3,0257 ± 0,202 |
|
6 |
0,120 ± 0,012 |
3600,000 ± 1,200 |
4,1104 ± 0,274 |
|
7 |
0,085 ± 0,009 |
4900,000 ± 1,400 |
5,1727 ± 0,345 |
|
8 |
0,060 ± 0,006 |
6400,000 ± 1,600 |
6,5248 ± 0,435 |
|
9 |
0,044 ± 0,004 |
8100,000 ± 1,800 |
8,0235 ± 0,535 |
На рис. 4.1 показан график экспериментальной зависимости Em = f1(z).
На рис. 4.2 приведен график линеаризованной зависимости (Em)-2/3 = f1(z2).
5. ВЫВОДЫ:
В результате проделанной работы получены экспериментальные данные по зависимости амплитудного значения э.д.с. измерительной катушки в зависимости от расстояния от центра по оси витка с током. Рассчитано амплитудное значение магнитной индукции в центре витка с током. Рассчитаны также погрешности прямых и косвенных измерений. При построении линеаризованной зависимости (Em)-2/3 = f1(z2) выяснилось, что прямая не проходит через полосы погрешностей. Это можно связать с недостаточной точностью измерительных приборов (большой систематической погрешностью осциллографа).
6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ
6.1. Что такое магнитное поле?
Магнитное поле – одно из частных проявлений электромагнитного поля. Магнитное поле создается движущимися электрическими зарядами, проводниками с током, телами и частицами, обладающими магнитным моментом. Изменяющееся во времени электрическое поле также создает магнитное поле. Магнитное поле действует только на то, что может создавать магнитное поле.
6.2. Какое из проявлений магнитного поля используется в данной работе при измерении магнитной индукции?
В данной работе использовано явление электромагнитной индукции. Переменный магнитный поток, создаваемый витком, питаемым переменным током, индуцирует в измерительной катушке э.д.с. индукции, измеряемую осциллографом.
6.3. Почему размеры измерительной катушки (ее поперечное сечение) должны быть значительно меньше размеров витка с током, создающего магнитное поле?
Так как значение магнитной индукции Bn является усредненным по площади сечения измерительной катушки и всегда меньше истинного значения магнитной индукции, а значит чем меньше поперечное сечение измерительной катушки, то тем ближе значение Bn к истинному значению индукции.
6.4. Как измерить амплитуду электрического сигнала с помощью осциллографа?
С помощью переключателя V/дел добиваются того, чтобы сигнал занимал на экране осциллографа максимальную площадь. Значением амплитуды сигнала является число делений на вертикальной шкале, которому соответствует максимум кривой на экране осциллографа.
6.5. По какому закону изменяется индукция магнитного поля на оси кругового тока? Записать этот закон.
Величина магнитной индукции на оси кругового тока описывается следующим законом:
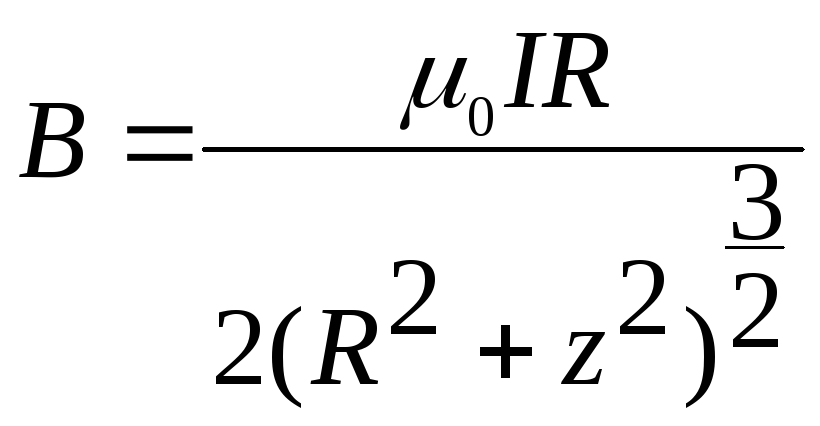 ,
,
где μ0 – магнитная постоянная;
I – величина тока, протекающего по витку;
R – радиус витка с током;
z – расстояние от центра витка по его оси.
Этот выражение можно вывести, используя закон Био-Савара-Лапласа и принцип суперпозиции.
6.6. Как проверить соответствие экспериментально измеренной зависимости Em(z) теоретической, т.е. закону Био-Савара-Лапласа?
Для этого надо, используя экспериментальные данные, построить график зависимости (Em)-2/3=f1(z2). Если точки в этой зависимости укладываются на прямую (в пределах их погрешностей), то экспериментальная зависимость Em = f1(z) соответствует теоретической, т.е. закону Био-Савара-Лапласа.
6.7. Какими способами можно построить прямую по экспериментальным точкам?
Прямую по экспериментальным точкам можно построить, используя метод наименьших квадратов.
