4.5. Решение уравнения

Все функции решаются после их линеаризации, то есть после приведения в линейную форму по отношению к переменным. Кривизна зависит от того, в какой форме представлены переменные.

Вычисление уравнения регрессии сводится к вычислению его коэффициентов (b₀, b₁ и т.д.). Основной способ нахождения коэффициентов уравнения – способ наименьших квадратов, (К. Гаусс, 1808 год, немецкий математик). Способ наименьших квадратов состоит в том, что коэффициенты уравнения выбираются так, чтобы сумма квадратов погрешностей (отклонений) была минимальной:

. (4.16)

Геометрически погрешности представляют собой разность между ординатой точки на линии регрессии и ординатой точки индивидуального наблюдения, обладающей той же абсциссой.

Если нужно определить вклад каждого из фактора в результативный показатель (в случае многофакторного уравнения), то решается уравнение без свободного члена b₀. Получится уравнение в β-коэффициентах:

у = β₁х₁ + β₂х₂ + … β_nх_n (4.17)

где β-коэффициенты – стандартизированные коэффициенты регрессии рассчитываются по формуле:

σ_x

β_i = b_i . ----- ,

σ_у

(4.18)

где b_i – значение коэффициента уравнения при факторном признаке;

σ_x – среднеквадратическое отклонение факторного признака;

σ_у – среднеквадратическое отклонение результативного признака.

β-коэффициент показывает, что если величина фактора изменится на одно среднеквадратическое отклонение, то зависимая переменная изменится соответственно на β своего квадратического отклонения при постоянстве остальных факторов. Наиболее существенный вклад в вариацию результативного признака обеспечивает тот фактор, для которого значение β-коэффициента наивысшее.

4.6. Статистическая оценка тесноты связи и существенности коэффициентов уравнения

Результаты решения представляются в следующем виде:

Таблица 4.2. Параметры уравнений регрессии и их оценка

Вид уравнения	Свободный член, b0	Коэффициент при независимой переменной, b1	Критерий Стьюдента, tx	Множественный коэффициент корреляции, R	Критерий Фишера, F
х3 = b0 + b1х6	5.619	0.133	13.033	0.725	169.862
х2 = b0 + b1х3	0.279	0.002	10.665	0.653	113.751
у = b0 + b1х2	-0.125	0.078	6.477	0.464	41.953

Результаты решения анализируются на предмет адекватности экономико-статистических моделей реальным причинно-следственным связям.

Теснота связи. Выводы о тесноте связи и существенности коэффициентов уравнения делаются на основе представления о порядке вычисления соответствующих показателей. Рассмотрим одну из формул для вычисления множественного коэффициента корреляции.

Как правило, компьютерные программы вычисляют множественный коэффициент корреляции R в квадрате. R² – коэффициент детерминации показывает долю систематической дисперсии, то есть вариацию результативного признака. В знаменателе формулы общая дисперсия – это сумма квадратов отклонений фактического значения от среднего значения. Общая дисперсия состоит из систематической и случайной дисперсии.

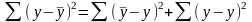, (4.19)

где 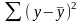– общая дисперсия, то есть сумма квадратов отклонений фактического значения от среднего значения;

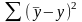– систематическая дисперсия, то есть сумма квадратов отклонений, вызванных влиянием учтенных факторов;

– случайная (остаточная) дисперсия, то есть сумма квадратов отклонений, вызванных влиянием неучтенных факторов.

Стандартная ошибка оценки представляет собой случайную дисперсию, распределенную на количество наблюдений, и вычисляется по формуле:

. (4.20)

Стандартная ошибка показывает, в каких пределах можно утверждать, что выборочная характеристика имеет место и в генеральной совокупности. Поэтому расчетное значение результативного признака нужно считать нормальным в пределах стандартной ошибки оценки: ŷ  Δy.

Расчетное значение результативного признака следует принимать в пределах от у – Δy до у + Δy.

Оценка существенности коэффициентов уравнения производится путем сравнения фактического t-отношения с табличным значением t-критерия Стьюдента. Коэффициент признается существенным, если t_х > t_0р, где p – вероятность (в экономических расчетах принимается равным 0,95). t-критерий представляет собой отношение значения коэффициента уравнения при переменной к его собственной ошибке:

, (4.21)

где μ_b – ошибка коэффициента регрессии.

Если фактическое значение t-статистики больше или равно табличному значению при определенном уровне вероятности, например, p = 0,95, то это значит, что в 95 % случаев изменение факторного признака будет существенно изменять результативный признак.

Общая проверка достоверности всех коэффициентов регрессии осуществляется на основе критерия Фишера: