Задача 7. Тема «Линейная корреляция и регрессия».

Для приведенных исходных данных постройте диаграмму рассеяния и определите по ней характер зависимости. Рассчитайте выборочный коэффициент корреляции Пирсона, проверьте его значимость при α=0,05. Запишите уравнение регрессии и дайте интерпретацию полученных результатов.

Компания, занимающаяся продажей радиоаппаратуры, установила на видеомагнитофон определенной модели цену, дифференцированную по регионам. Исследуйте зависимость объема продаж (Y, шт.) от цены (Х, тыс. руб.) по выборочным данным из 8 регионов.

Х	5,5	6,0	6,5	6,0	5,0	6,5	4,5	5,0
Y	420	380	350	400	440	380	450	420

Решение:

Факторной переменной в нашей задаче является Х – цена видеомагнитофона, откликом является Y – объем продаж. Построим диаграмму рассеяния (рисунок 7.1) по имеющимся данным.

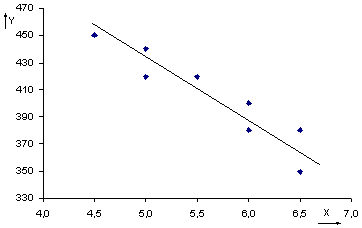
Рисунок 7.1 – Диаграмма рассеяния.

По виду диаграммы есть основания предполагать достаточно сильную линейную отрицательную зависимость объема продаж от цены.

Для расчета коэффициентов регрессии по формулам найдем средние значения:

, ,

найдем несмещенные оценки дисперсий:

, ,

и оценку коэффициента корреляции Пирсона:

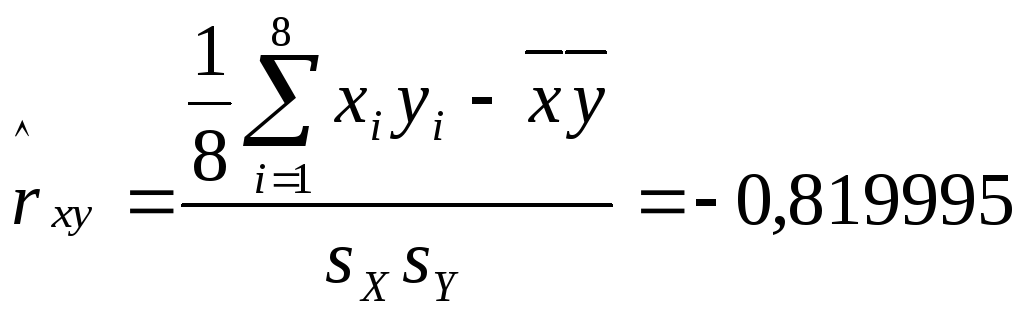
Коэффициент Пирсона достаточно близок к единице и имеет отрицательное значение, значит можно утверждать об отрицательной связи между объемом продаж и ценой на товары.

Найдем коэффициенты b₀ и b₁ уравнения регрессии:

где - средние значения переменных Х и Y, рассчитанные по выборке;

- несмещенные оценки дисперсий Х и Y;

- оценка коэффициента корреляции Пирсона.

Таким образом, уравнение регрессии Y на Х имеет вид

Коэффициент b₁ характеризует наклон линии регрессии и значение показывает, что при увеличении Х на единицу ожидаемое значение Y уменьшается на 37,25711. Полученная регрессионная модель указывает на то, что каждое увеличение цены видеомагнитофона на 1 тысячу рублей уменьшает объем их продаж на 37,25711. Отсюда b₁ может интерпретироваться как изменение объема продаж, который изменяется в зависимости от изменения цены на видеомагнитофоны.

Свободный член b₀ в уравнении – это значение Y при Х=0. Поскольку маловероятно, что цена видеомагнитофона равна нулю, то можно рассматривать b₀ как меру влияния на величину объема продаж других факторов, не включенных в уравнение регрессии. Это влияние можно объяснить и с помощью коэффициента детерминации:

,

Для линейной модели коэффициент характеризует долю объясняемого моделью разброса экспериментальных данных. В нашем примере модель учитывает 67,23% изменения выручки

магазина. И 32,7% разброса объясняются факторами, не включенными в уравнение регрессии.

Коэффициент эластичности для нашей модели вычисляем по формуле:

,

то есть при увеличении средней цены на видеомагнитофон на 1% объем их продаж в среднем уменьшается на 0,517%.

Так как исходная выборка малого объема, проверим значимость коэффициента корреляции. Основная гипотеза Н₀ состоит в том, что коэффициент корреляции не значим Н₀: то есть между переменными Х и Y нет линейной связи. Альтернативная гипотеза Н₁: - коэффициент корреляции значим, и переменные Х и Y связаны отрицательной линейной зависимостью.

Наблюдаемое значение статистики К равно:

Согласно заданному уровню значимости α=0,05 определим границу критической области по таблице распределения Стьюдента. По виду альтернативной гипотезы заключаем, что критическая область является левосторонней: (-∞; -К_кр]. Значение К_кр находим по таблице распределения Стьюдента:

.

Наблюдаемое значение попадает в критическую область (-∞; -1,94], поэтому основную гипотезу следует отвергнуть в пользу альтернативной: связь между переменными Х и Y значима.

Данные наблюдений на уровне значимости α=0,05 говорят о том, что объем продаж видеомагнитофонов в среднем линейно убывает при увеличении цены на него.