Контрольные вопросы:

1. Что такое абсолютные величины и каково из значение? Приведите примеры абсолютных величин.

2. В каких единицах измерения выражаются абсолютные величины? Приведите примеры.

3. Всегда ли для анализа изучаемого явления достаточно одних абсолютных показателей?

4. Что называется относительными величинами?

5. На какие виды подразделяются относительные величины?

6. Дайте определение понятию относительная величина структуры, раскройте цели ее применения.

7. Что такое относительная величина интенсивности и чем она отличается от других видов относительных величин?

8. Что такое относительная величина координации?

9. Что такое базисные и цепные относительные величины динамики?

10. Дайте характеристику относительной величины сравнения.

Тема: Средние величины в статистике

Вопросы:

1. Понятие о средних величинах

2. Средняя арифметическая величина

3.Расчет средней арифметической в рядах распределения

4. Основные свойства средней арифметической

5. Расчет показателей способом моментов

6.Средняя гармоническая

7.Правило мажорантности степенных средних в статистике

8. Средняя геометрическая

1. Наряду с абсолютными и относительными величинами в статистике большое применение находят средние величины. В повседневной жизни употребляются термины «в среднем», «средняя». Например, средняя цена, средняя заработная плата, средний размер сбережений и т.д.

В экономическом анализе часто приходится оперировать средними величинами в целях лучшего изучения общей картины, когда нужно из многих признаков получить величину, в которой отражались бы свойства всех признаков, входящих в состав совокупности.

Средняя величина – обобщающая количественная характеристика однородных явлений по какому- либо варьирующему признаку.

Применение средних величин позволяет охарактеризовать определенный признак совокупности одним числом, несмотря на количественные различия единиц по данному признаку внутри совокупности.

В статистике средние величины подразделяются на два больших класса:

• степенные средние (средняя арифметическая, средняя гармоническая и т.д.);

• структурные средние (мода и медиана).

2. Наиболее распространенным видом средних величин является средняя арифметическая. Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц.

Средняя арифметическая применяется в форме простой средней и взвешенной средней.

• Средняя арифметическая простая равна сумме всех значений данного признака поделенной на число единиц, обладающих этим признаком.

ар=

где х1,х2 …хn –индивидуальные значения варьирующего признака (варианты);

n – число единиц совокупности.

Например, требуется найти среднюю выработку одного рабочего (слесаря), если известно, сколько деталей изготовил каждый из 15 рабочих, т.е. дан ряд индивидуальных значений признака, шт.: 21 ,20 ,20 ,19 ,21 ,19 ,18 ,22 ,19 ,20 ,21 ,20 ,18 ,19 ,20.

= (21+20+20+19+21+19+18+22+19+20+21+20+18+19+20)/15= 20

Средняя из вариантов, которые повторяются различное число раз, или , как говорят, имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в различных группах совокупности ( в группу объединяют одинаковые варианты).

• Средняя арифметическая взвешенная – это частное от деления суммы произведений вариантов и соответствующих им частот на сумму всех частот.

ар=

где х – варианты;

f- частота.

Частоты (f) принято называть весами, вследствие чего средняя арифметическая, вычисленная с учетом весов, и получила название взвешенной.

Например, технику вычисления данной средней проиллюстрируем на рассмотренном выше примере. Для этого сгруппируем исходные данные и поместим в таблицу:

Распределение рабочих по выработке деталей

Выработка деталей за смену одним рабочим, шт.(х)	Число рабочих (веса) (f)	Х * f
18 19 20 21 22	2 4 5 3 1	36 76 100 63 22
Итого	15	297

= (36+76+ 100+63+22) /15=20

Однако в ряде случаев абсолютные частоты отсутствуют, а известны относительные частоты, или, как принято их называть, частости, которые показывают долю или удельный вес частот во всей совокупности.

Расчет производится тем же способом, однако, так как средняя величина увеличена в 100 раз, полученный результат следует разделить на 100.

В нашем примере сначала определяют удельный вес числа рабочих :

Выработка деталей за смену одним рабочим, шт (х)	18	19	20	21	22
Удельный вес числа рабочих в общей численности (f), %	13,4	26,6	33,4	20	6,6

Тогда, = (18*13,4+19*26,6+20*33,4+21*20+22*6,6)/100= 20.

Следовательно, теперь получится та же величина средней, однако вместо частот будут использованы удельные веса (частости).

3. Если значения осредняемого признака заданы в виде интервалов («от – до»), т.е. интервальных рядов распределения, то при расчете средней арифметической величины в качестве значений признаков в группах принимаются середины этих интервалов, в результате чего образуется дискретный ряд.

Например,

Распределение рабочих АО по уровню оплаты труда

Исходные данные		Расчетные данные
Группы рабочих по оплате труда, руб.	Число рабочих, чел., (f)	Середина интервала, руб . (х)	Х * f
До 1000 1000 – 1200 1200 – 1400 1400 – 1600 1600 – 1800 1800 и более	5 15 20 30 16 14	900 1100 1300 1500 1700 1900	4500 16500 26000 45000 27200 26600
Итого	100	-	145800

Однако первый и последний интервал даны открытыми: в первом отсутствует нижняя граница, а в последнем - верхняя.

Исчисление средних по данным интервальных рядов с закрытыми интервалами производится по формуле средней арифметической простой, т.е. для второго интервала х 2= (1000+1200)/ 2 =1100 руб.

Для АО в группе рабочих до 1000 руб. условно считаем , что этот интервал равен последующему, т.е.200 руб. ( 1200-1000), затем от 1000 руб. вычитаем 200 руб. и находим нижнюю границу первого интервала, которая будет равна 800 руб. (1000- 200). Затеи расчет ведется так же, как и для второй группы, т.е. по формуле средней арифметической простой.

=145800/100= 1458

Средний уровень оплаты труда рабочих АО составляет 1458 руб. в месяц.

4.Основные свойства средней арифметической:

• Если все варианты уменьшить или увеличить на одно и то же постоянное число, то средняя арифметическая из этих вариант уменьшится или увеличится на то же самое число.

Пример. Пусть з/ пл каждого работника фирмы «Весна» увеличилась за некоторый период на 150 руб. Тогда средняя з/пл всех работников фирмы увеличилась также на 150 руб.

• Если все варианты одинаково увеличить или уменьшить в одно и тоже число раз, то средняя арифметическая увеличится ( или уменьшится) во столько же раз.

Пример. Так, если бы заработная плата каждого работника фирмы «Весна» увеличилась на 10 %, то и средняя заработная плата всех работников фирмы увеличилась бы на 10%.

• Если же все веса средней одинаково увеличить (или уменьшить) в несколько раз, средняя арифметическая не изменится.

Увеличение всех весов в несколько раз приводит к тому, что во столько же одновременно увеличится и числитель, и знаменатель дроби (средней арифметической), поэтому значение дроби не изменится.

5. В качестве весов средней вместо абсолютных показателей можно использовать удельные веса в общем итоге (доли или проценты). Тем самым достигается упрощение расчетов средней.

Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот. Наибольшее упрощение достигается когда в качестве А выбирается значение одного из центральных вариантов обладающего наибольшей частотой в качестве i- величина интервала (для рядов с одинаковыми интервалами). Величина А называется началом отсчета поэтому такой метод вычисления средней называется «способом отсчета от условного нуля» или «способом моментов».

Допустим что все варианты х сначала уменьшены на одно и то же число А, а затем уменьшены в i раз. Получим новый вариационный ряд распределения новых вариантов ( ).

Тогда новые варианты будут выражаться : = , а их новая средняя арифметическая m1- момент первого порядка- формулой m1= и будет равна средней из первоначальных вариантов, уменьшенной сначала на А, а затем в I раз, т.е. m1= .

Для получения действительной средней надо момент первого порядка m1 умножить на I и прибавить А :

ар=m1*i+А =

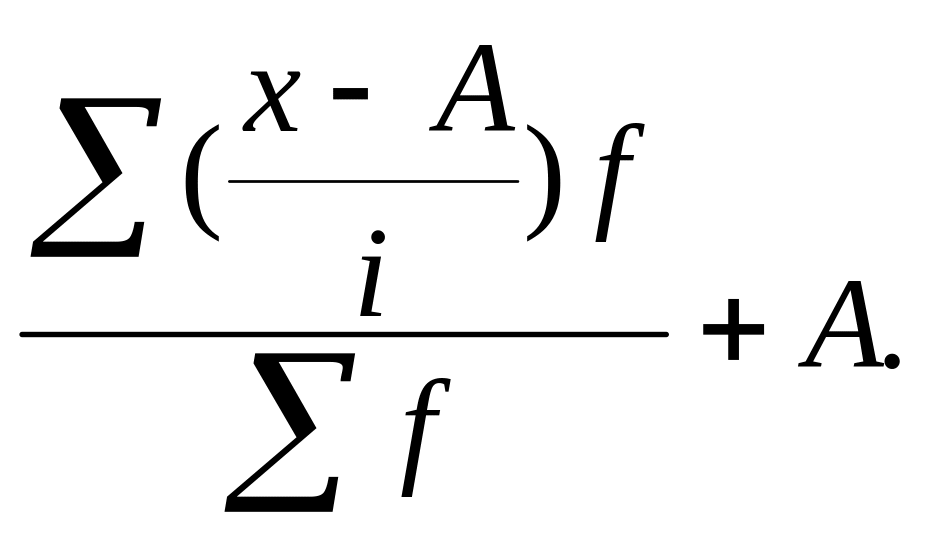
Данный способ вычисления средней арифметической из вариационного ряда называют «способом моментов». Применяется этот способ в рядах с равными интервалами.

Например: имеются следующие данные: