Требуемая площадь сечения

A_тр=N/(_eR_y_c)=342,6 10/(0,089 230)=167,37 см ²

Компоновка сечения

Предварительно принимаем толщину полок t_f =1,4 см, тогда высота стенки колонны:

h_w=h-2 t_f= 50-2 1,4=47,2 см.

Минимальная толщина стенки из условия местной устойчивости при 0,8 и m  1.

t_{w min}=(h_w)/[(0,9+0,5) (E/R_y)]=(47,2)/ [(0,9+0,5 1,91) 2,06 10⁵/230)] =0,85 см.

Принимаем: t_w =1 см (h_w / t_w =80….120). Включаем в расчетную площадь сечения колонны два крайних участка стенки шириной:

Расчетная площадь сечения стенки:

A_w= 1х47,2 =47,2 см²

Требуемая площадь полки:

A_{f тр}=(A_тр-A_w)/2= (167,37-47,2)/2=60,085 см²

Из условия устойчивости верхней колонны из плоскости действия момента ширина полки:

b_{f min}=l_efy^в/20=320/20=16 см

а из условия местной устойчивости сжатой полки

(b_ef/t_f)  [(0,36+0,1_х) (E/Ry)]=(0,36+0,1∙1,91) ∙ 2,06∙10⁵/230=16,49

где b_ef = (b_f-t_w)/ 2

Принимаем b_f = 40 см; t_f =1,6 см.

b_f /t_w =( b_f-t_w)/(2 ∙ t_f)= (40-1)/(2∙1,6)=12,19 17,93

A_f=40 ∙ 1,6=64 см²

Геометрические характеристики сечения

Полная площадь сечения :

A₀=2 b_f t_f + h_w ∙ t_w=2∙40∙1,6+46,8∙1=174,8 см²

где h_w=h-2 t_f=50-2∙1,6=46,8 см

Расчетная площадь сечения при учете только устойчивой части стенки

A=2b_f ·t_f + A_w =2·40·1,6+47,2=175,2 cм²>167,37 cм²

При определении геометрических характеристик учитывается полное сечение:

I_x= t_w h_w³/12 + 2 ∙ b_f ∙ t_f ∙ (h/2- t_f / 2)²= 1∙46,8³/12+2∙40∙1,6∙ (50/2-1,6/2)²=

=83503,856 см ⁴

I_y=2 t_f b_f³/12=2∙1,6∙40³/12 = 17066,67 см ⁴

W_x=I_x/0,5h=83503,856 /0,5 ∙ 50=3340,15 см³

_x=W_x/A₀=3340,15 /174,8 =19,12 см

i_x= I_x/A₀=83503,856 /174,8 =21,85 см

i_y= I_y/A₀=17066.67 /174,8 =9,88 см

A_f/A_w= 40∙1,6/1∙46,8=2,15

Проверка устойчивости верхней части колонны в плоскости действия момента (относительно оси х-х):

= l_efx^в/ i_x=1200/21,85=54,92

=_х E/R_y= 54,92230/(2,06∙10⁵) =1,835

m_x=e_x/_x=183/19,12=9,57

Так как A_f/A_w1; 5<m<20 (см. табл.7 приложения)

=1,4-0,02 ∙ _x=1,4-0,02∙1,835=1,3633

m_ef =  ∙ m_x = 1,3633∙9,57=13,05

Из табл.8 приложения находим _е=0,1005.

Проверим устойчивость сечения

б=N/(_е A)=342,6∙10/(0,1005∙167,37) = 203,68 МПа  Ry=230 МПа

Недонапряжение составляет:

(230-203,68)/230∙100=11,44%  5 % поэтому уменьшаем толщину полки t_f=1,4 cм.

b_f /t_w =( b_f-t_w)/(2 ∙ t_f)= (40-1)/(2∙1,4)=13,9318,19

A_f=40 ∙ 1,4=56 см²

Полная площадь сечения :

A₀=2 b_f t_f + h_w ∙ t_w=2∙40∙1,4+47,2∙1=159,2 см²

где h_w=h-2 t_f=50-2∙1,4=47,2 см

Расчетная площадь сечения при учете только устойчивой части стенки

A=2b_f ·t_f + A_w =2·40·1,4+47,2=159,2 cм²

При определении геометрических характеристик учитывается полное сечение:

I_x= t_w h_w³/12 + 2 ∙ b_f ∙ t_f ∙ (h/2- t_f / 2)²= 1∙47,2³/12+2∙40∙1,4∙ (50/2-1,4/2)²=

=74897,717 см ⁴

I_y=2 t_f b_f³/12=2∙1,4∙40³/12 = 14933,33 см ⁴

W_x=I_x/0,5h=74897,717/0,5 ∙ 50=2995,88 см³

_x=W_x/A₀=2995,88/159,2=18,82 см

i_x= i_x/A₀=74897,717/159,2=21,69 см

i_y= i_y/A₀=14933,33/159,2=9,68 см

A_f/A_w= 40∙1,4/1∙47,2=1,186

Проверка устойчивости верхней части колонны в плоскости действия момента (относительно оси х-х):

= l_efх^в/ i_x=1200/21,69=55,325

=_х R_y / E = 55,325230/(2,06∙10⁵) =1,85

m_x=e_x/_x=183/18,82=9,72

Так как A_f/A_w1; 5<m<20 (см. табл.7 приложения)

=1,4-0,02 ∙ _x=1,4-0,02∙1,85=1,363

m_ef =  x m_x = 1,363∙9,72=13,25

Из табл.8 приложения находим _е=0,094.

Проверим устойчивость сечения:

δ=N/(_е A)=342,6∙10/(0,094∙159,2) = 228,94 МПа  Ry=230 МПа

Недонапряжение составляет:

(230-228,94)/230∙100=0,46% < 5 %

УСЛОВИЕ ВЫПОЛНЯЕТСЯ!

Проверка устойчивости верхней части колонны из плоскости действия момента (относительно оси У-У)

Расчетный момент в сечении 2-2 соответствующий сочетанию нагрузок сечения 1-1 (1, 2, 3*,4(-М),5* )

М₂=-88-130+28-32-79=-301 кН м

Максимальный момент в пределах средней трети расчетной длины стержня

М_х=M₂ + (M₁-M₂)/H_в ∙ (H_в - l_efy^в/3)= -301+(-627,341)-(-301)/4∙ (4-

-3,2/3)=-362,97 кНм

Значение М_х принимается не менее половины наибольшего по длине стержня момента

М_х=-322,97 кНм  M_max/2=627,341/2=313,67 кНм

m_х= M_xA₀/(NW_x)=322,97∙159,2/(342,6∙2995,88)=5,01 см

при 5≤ m_х: С=С₅=β/(1+αm_х)

=0,65 + 0,05 m_х=0,65+0,05∙5=0,9

_y= l_efy^в/i_y= 320/9,68=33,06

_c=3,14E/R_y=3,14 206000/230=94

При _y =33,06<_С=94

С₅=β/(1+αm_х)=1/(1+0,9·5)=0,18

Коэффициент снижения расчетного сопротивления при потере устойчивости балок в большинстве случаев при проверке устойчивости колонн принимается _в =1

При _y =33,06; 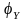=0,922

h_w/t_w=47,2/1=47,2 <3,8 E/R_y=3,8206000/230=114

поэтому в расчетное сечение включается только часть стенки

=N/(С ∙ _y ∙ A₀)=342,6∙10/(0,18∙0,9∙159,2)=132,84 МПа R_y=230 МПа

УСЛОВИЕ ВЫПОЛНЯЕТСЯ!

Подбор сечения нижней (подкрановой) части колонны

Расчетные комбинации усилий (сечения 3-3, 4-4)

М₁= - 304 кН, N₁= - 365,6 кН (нагрузки (1,3,4 (-М));

М₂= 1073 кН, N₂ = - 892,6 кН (нагрузки (1,2,3,4(+М),5*);

Сечение нижней части колонны сквозное, состоящие из двух ветвей, соединенных решеткой. Подкрановую ветвь ее принимаем из широкополочного двутавра, а наружную – составного сварного сечения из трех листов.

Определим ориентировочное положение центра тяжести. Принимаем z₀=5см.

h₀=h_H - z₀=100-5=95 см

y₁=[M₂ /M₁ +M₂] ∙ h₀=1073/(304+1073)∙95=77,9 см

у₂ = h₀ - у₁ = 95 – 77,9 = 17,1 см.

Усилие в наружной ветви:

N_в2= | N₂| у₁/ h ₀+ M₂/ h ₀ =892,6∙77,9/95+107300/95=1861,4 кН

Усилие в подкрановой ветви:

N_в1= | N₁| у₂/ h ₀+ M₁/ h ₀ =365,6 ∙ 17,1/95 + 30400/95=385,81 кН

Определяем требуемую площадь ветвей и назначаем сечение. Из условия устойчивости при центральном сжатии для подкрановой ветви:

А_в1= N_в1/  R_yγ_с γ_с=1,0

значение коэффициента  можно принимать в пределах  = 0,7...0,9, тогда:

А_в1= 385,81 ∙ 10/(0,8 ∙ 230) = 20,97 см²

По сортаменту (табл. 10 приложения) подбираем двутавр N 30Б1

А_в1= 41,92 см²; i_х1= 3,05 cм; i_y1 =12,29 см.

Для наружной ветви:

А_в2= N_в2/  R_yγ_с = 1861,4∙10/(0,8 ∙ 230) = 101,163 см²

Для удобства прикрепления элементов решетки расстояние между внутренними гранями полок принимаем таким же, как в подкрановой ветви:

h _w’= h –2t=295- 2 ∙ 8,5 =278 мм,

где h,t соответственно высота сечения подкрановой ветви и толщина ее полки.

Толщину стенки швеллера для удобства соединения ее вcтык c полкой подкрановой части колонны, принимаем равной t _w = 10 мм, т.е. одинаковый c толщиной полки надкрановой части. А высоту стенки швеллера назначаем с учетом толщины полок и сварных швов h _w =325 мм.

Требуемая площадь полок:

А_f= (А_в2- t _w h _w)/2=(101,163 – 1 ∙32,5)/2=34,3 см²

Из условия местной устойчивости полки швеллера (при = 0,8...4)

_{bf (0,43+0,08)  E/Ry≈15}

b_f = 15∙t_f; b_f = t_f ∙15t_f =34,3 см²; t_f 34,3/15=1,50 см.

принимаем t_f =2 см: А_f/t_f = 34,3/2 =17,15 см

Принимаем b_f =20 см.

_{Геометрические характеристики ветви:}

А_в2= t _w h _w +2 _{bf tf =1∙32,5+2∙20∙2=112,5 см2}

z₀= (t _w h _w 0,5 t _w +2 b_f t_f (0,5 b_f+ t_w) )/А_в2=(1∙32,5∙0,5∙1+

+2∙2∙20(0,5∙20+1))/_112,5 = 7,97 см

I _X2 = t _w h _w (z₀-0,5 t _w)²+2 b_f t_f(0,5 z₂ -0,5 z₁) ²+ 2t_f b_f³ / 12.

_{Где :} z₁₌ z₀ - t _w= 7,97-1=6,97 см

z₂ = _{bf - z1 = 20-6,97=13,03 см}

I _X2 = 1∙32,5∙ (7,97-0,5∙1)²+2∙20∙2∙(0,5∙13,03-0,5∙6,97)²+ 2∙2∙20³/12=

=5214,67 см⁴

I _у = t _w h _w³ /12+2t_f b_f((h _w’ + t _w)/2)²= 1∙32,5³/12 + 2∙2 ∙20∙ ((27,8+

+1)/2)²=19449,5 см ⁴

i_х2 = _ I _X2/ А_в2= _5214,67_{/112,5 =6,8 см;}

i_у = _ I _у/ А_в2= _19449,5 _{/112,5 = 13,15 см.}

Уточняем положение центра тяжести сечения колонны:

h₀=h_H - z₀=100-7,97=92,03 см

_{у1 =} А_в2/ ₍А_в1 + А _в2) ∙ h₀= _112,5 /(41,92+_112,5) ∙92,03=67,05 см

у₂ = h₀- у₁ = 92,03-67,05=24,98 см.

Отличие от первоначально принятых размеров мало, поэтому усилия в ветвях не пересчитываем.