Завдання 4

Опишіть множини, що відповідають зафарбованої частині кожної діаграми Венна (рис. 9.1):

1 2

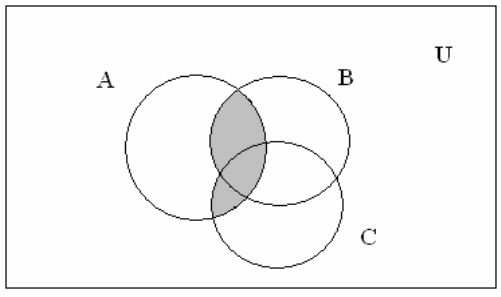
3 4

5 6

7 8

9 10

Завдання 5

Знайти істинностне значення кожного з наступних висловлень:

1 PQ~ RP R, якщо P 1, Q 1, R 0.

2 ~ Q~ RPQ , якщо P 0, Q 1, R 0.

3 P R~ Q~ PQ R, якщо P 1, Q 1, R 1.

4 QR ~ P RQ, якщо P 0, Q 1, R 1.

5 ~ Q~ RQPR P, якщо P 0, Q 0, R 0.

6 , PQPRQPякщо P 1, Q 1, R 1.

7 ~ P R~ QPQ~ R, якщо P 1, Q 1, R 0.

8 P~ RQ~ RP R, якщо P 0, Q 1, R 0.

9 ~ Q~ RP QR, якщо P 1, Q 1, R 0.

10 R~ P~ RQ~ R , якщо P 0, Q 1, R 0.

Завдання 6

Скласти таблицю істинності для кожного з наступних висловлень:

1 RP~ RQ P.

2 R~ QP Q~ R.

3 QP~ Q PR.

4 PPQ~ R P.

5 Q~ RP Q~ R.

6 P~ RP~ Q R.

7 QPQ~ R P.

8 PQR~ Q P.

9 RPQRQ P.

10 Q P R~ Q P.

Завдання 7

Обчислити значення функцій на зазначених наборах:

1 __x₁, x₂),₁₁(x₃, x₂)), 0,1,0.

2₁₃₈(x₃,x₁),₁(x₂, x₁)), 1,1,0.

3 ₁₁(₂(x₃), ₇(x₁,x₂)), 0,0,1.

4 ₇(₄(x₃,x₁),₃(x₂)), 0,1,1.

5 ₁₃(₁(x₁,x₂),₃(x₃)), 0,0,0.

6 ₂(₂(x₁),₆(x₂,x₃)), 1,0,1.

7 ₈(₃(x₁),₆(x₃,x₂)), 1,1,1.

8 ₅(₁(x₃,x₂),₉(x₁,x₂)), 1,1,0.

9 ₂(₅(x₃,x₂),₄(x₁)), 0,1,1.

10 ₇(₁₀(x₁,x₃), ₃(x₂,x₁)), 1,0,0.

Завдання 8

Логічну функцію представити булевою формулою у вигляді ДДНФ і ДКНФ:

1 fx₁,x₂,x₃)=( ₁x₂)(x₃1).

2 fx₁,x₂,x₃)x₁|( ).

3 fx₁,x₂,x₃)x₁x₂)(x₃x₁).

4 fx₁,x₂,x₃)x₃x_{1 2}).

5 fx₁,x₂,x₃)( ) x₃.

6 fx₁,x₂,x₃)x₁1)( ₂x₃).

7 fx₁,x₂,x₃)x_{1 3})|( ₂x₃).

8 fx₁,x₂,x₃)x₁x₂) 

9 fx₁,x₂,x₃)x₁x₃ ₂).

10 fx₁,x₂,x₃)x₁|x₂) ₃.

Завдання 9

Визначити доповнення 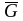графів G, зображених на рис. 2.2. Побудувати повні графи.

Варіант 1 Варіант 2

Варіант 3 Варіант 4

Варіант 5 Варіант 6

Варіант 7 Варіант 8

Варіант 9 Варіант 10

Рисунок 2.2 - Графи для завдання 10

Завдання 10

Для неорієнтованого графу G, зображеного на рисунку 2.3, виконати вказані операції видалення вершин та ребер.

Побудувати отриманий граф. Скласти матрицю суміжності на матрицю інцидентності. Написати маршрут, ланцюг, простий ланцюг, цикл, простий цикл. Знайти:

а) число вершин і число ребер;

б) степені всіх вершин.

Рисунок 2.3 - Неорієнтований граф G

№ варіанта	Видалити в графі G вершини {i}	Видалити в графі G ребра {(i,j)}
1	{1;3;9}	{(6;7);(7;10);(10;11);(10;13)}
2	{2;3;13}	{(4;8);(6;7);(7;8);(10;11)}
3	{4;5;9}	{(1;2);(6;10);(10;11);(11;13)}
4	{5;9;11}	{(1;4);(4;7);(4;8);(10;13)}
5	{2;8;10}	{(3;7);(4;7);(9;12);(12;13)}
6	{3;10;12}	{(2;5);(2;6);(8;9);(7;11)}
7	{5;10;11}	{(1;4);(4;7);(4;8);(9;12)}
8	{3;4;13}	{(2;5);(6;10);(10;11);(11;12)}
9	{1;8;12}	{(2;7);(5;6);(6;7);(10;13)}
10	{2;8;13}	{(3;7);(6;7);(9;12);(11;12)}