6. Результаты расчёта

• Крутящий момент M_K = 1,59e6 Н∙мм;

• Максимальное локальное напряжение = 87,1 МПа (не учитывается, поскольку не влияет на общий уровень напряжений);

• = 50 МПа;

• Момент сопротивлению кручению 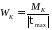= 3.19e4 мм³;

• Характеристики стержня при кручении второго рода J_K = 3,19e6  мм⁴.

Полученные характеристики J_K, W_K учтены в таблице Таблица 2.

5. Расчёт состояния рамы

   1. Допущения

Физические допущения:

• Крепление стержней абсолютно жёсткие;

• Используется критерий «Хубера-Мизеса»; для определения эквивалентных напряжений

• Весовая нагрузка, приложенная к пластине опоры равномерно разносится на четыре её угла;

Моделирование стержней балки проводится в программе ANSYS с помощью элементов BEAM 188 учитывающих изгиб и сдвиг в двух направлениях, а так же угловые деформации скручивания. Система координат конечного элемента BEAM 188, в которой программа предоставляет результаты расчёта, представлена на рисунке Рисунок 7.

Рисунок 7. Система координат балочного элемента

2. Геометрическая модель рамы

Схематичное изображение рамы показано на рисунке Рисунок 8. На рисунке показана нагрузка, приведённая к точкам рамы и внешние закрепления.

Рисунок 8. Геометрическая модель рамы

3. Мкэ модель

Вид рамы после разбивки на конечные элементы приведён на рисунке Рисунок 9.

Рисунок 9. Конечно-элементная модель рамы

6. Расчёт прочности и жёсткости рамы

Рама является плоско-пространственной. Поэтому существенными силовыми факторами в ней будут изгибающий, относительно оси Y (Рисунок 7) момент M_y и крутящий момент M_k. Некоторые стержни рамы являются короткими и ,строго говоря, они должны рассчитываться на сдвиг под действием поперечной силы, однако для используемого профиля достаточно сложно определить коэффициенты пропорциональности Q_z и τ_xz. Поэтому в расчёте учитывается только изгибающий и крутящий моменты.

1. Нагружение «А»

1. Картина прогибов при нагружении «А»

Картина перемещений представлена ниже (Рисунок 10).

Рисунок 10. Прогибы балок рамы u, мм. Максимальное перемещение umax=1,85 мм.

2. Эпюры моментов при нагружении «А»

Ниже приведены эпюры изгибающего M_Y (Рисунок 11) и крутящего M_K (Рисунок 12) моментов.

Рисунок 11. Изгибающий момент MY, Н·мм, максимальное значение MY,=985 Н·м

Рисунок 12. Крутящий момент MK, Н·мм максимальное значение MK=106 Нм MK,=10 600 Н·мм

3. Эпюра эквивалентных напряжений при нагружении «А»

Для упрощения расчётов предполагается, что в пределах каждого сечения максимальное напряжение от изгиба и кручения достигаются в одной точке. Данное допущение идёт в запас. Тогда эквивалентное напряжение можно вычислить на основании критерия Хубера-Мизиса можно вычислить по формуле:

(8)

Распределение эквивалентных напряжений, вычисленных по формуле (8) представлено на рисунке Рисунок 13.

Рисунок 13. Эпюра эквивалентных напряжений σe, МПа максимальное значение σe=14,1 МПа

2. Нагружение «Б»

   1. Картина прогибов при нагружении «Б»

Картина перемещений представлена ниже (Рисунок 14).

Рисунок 14. Прогибы балок рамы u, мм. Максимальное перемещение umax=1,81 мм.

2. Эпюры моментов при нагружении «Б»

Ниже приведены эпюры изгибающего M_Y (Рисунок 15) и крутящего M_K (Рисунок 16) моментов.

Рисунок 15. Изгибающий момент MY, Н·мм, максимальное значение MY,=861 Н·м

Рисунок 16. Крутящий момент MK, Н·мм, максимальное значение MK=90 Н·м

3. Эпюра эквивалентных напряжений при нагружении «Б»

Распределение эквивалентных напряжений, вычисленных по формуле (8) представлено на рисунке Рисунок 17.

Рисунок 17. Эпюра эквивалентных напряжений σe, МПа максимальное значение σe,=12,2 МПа,

3. Выводы и рекомендации

1. Численные результаты расчёта представлены в таблице Таблица 3.

Таблица 3. Результаты расчёта

	А	Б
Максимальное перемещение umax, мм	1,85	1,81
Максимальное эквивалентное напряжение σe, мм	14,1	12,2
Коэффициент запаса по текучести, nT	14	16

2. Рама преимущественно работает на изгиб: изгибающие момент на порядок больше крутящего. Необходимо обеспечить с помощью креплений достаточно жёсткую передачу изгибающего момента.

3. В расчёте не учтены действия локальных концентраций напряжений и действия поперечных, сдвигающих сил, массы самих стержней и нагрузки на раму от веса дополнительного оборудования и персонала. Поэтому полученные достаточно большие значения коэффициенты запаса можно считать приемлемыми.

4. Смещения кареток слабо влияет на напряжения и деформации, поскольку их вес мал по сравнению со станиной. Наиболее опасное состояние, по-видимому, когда центр масс конструкции ближе всего к центру рамы. Смещение нагрузки к краям или добавление нагрузки на краю (например, от массы персонала) не значительно будет влиять на напряжённо-деформированное состояние.