10. Связь коэффициента диффузии с подвижностью частицы

Понятием подвижности используется для рассмотрения многих процессов, но смысл его всегда один и тот же. Например, при построении теории броуновского движения это понятие применялось к броуновским частицам, движущимся в жидкости под действием постоянных сил. На движущуюся в жидкости частицу действует сила сопротивления, пропорциональная скорости движения частицы. Подвижностью называется коэффициент этой пропорциональности:

.

Но оно применимо и к частицам молекулярных и атомных размеров, например к ионам, движущимся в электролите. На заряженный ион в постоянном электрическом поле действует постоянная сила F, пропорциональная напряженности электрического поля. Кроме того, при движении ион испытывает столкновения с окружающими молекулами и ионами. При отсутствии внешней силы F движение иона было бы полностью беспорядочным. При наличии постоянной силы F появляется преимущественное направление скорости иона. На беспорядочное тепловое движение накладывается регулярное движение в направлении силы F. Если электрическое поле не очень сильное, то установившаяся скорость иона пропорциональна приложенной к нему силе F. То есть в общем подвижностью частицы называется коэффициент пропорциональности В между регулярной скоростью и силой.

Допустим теперь, что имеется «газ» каких-то частиц в постоянном и однородном силовом поле. «Газ» настолько разрежен, что силами взаимодействия между его частицами можно полностью пренебречь. Примером такого «газа» может служить совокупность броуновских частиц, взвешенных в жидкости. Другим примером является обычный идеальный газ в силовом поле. Если F — сила, действующая на частицу «газа» в силовом поле, то потенциальная энергия ее в этом поле будет

.

(Предполагается, что ось X направлена в сторону действующей силы.) Если состояние стационарно, то концентрация частиц «газа» меняется в пространстве в соответствии с формулой Больцмана, которую можно получить из барометрических формул (давление в газе в поле силы тяжести, Универсальная газовая постоянная выражается через произведение постоянной Больцмана на число Авогадро):

, :

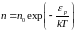
Но микропроцессы не прекращаются даже тогда, когда состояние стационарно. Поскольку есть градиент концентрации, в газе происходит диффузия. Диффузионный поток в положительном направлении оси X определяется выражением

.

А так как «газ» находится в силовом поле, то существует также и «силовой поток» молекул с плотностью

.

В состоянии равновесия должно быть

.

Подставляя сюда распределение Больцмана, получаем после сокращения на n

.

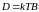Зто соотношение между коэффициентом диффузии и подвижностью частицы было установлено Эйнштейном и носит его имя.

10. Концентрационная диффузия в газах

Рассмотрим теперь смесь двух различных газов с концентрациями п₁ и п₂, изменяющимися в направлении оси X. Давление и температура смеси предполагаются постоянными, так что общая концентрация – одна и та же во всем газе. Диффузионные потоки газов определяются выражениями

, ,

где D₁₂ – коэффициент диффузии газа 1 в газ 2, a D₂₁ — коэффициент диффузии газа 2 в газ 1. Благодаря наличию диффузионных потоков на тепловое движение газов накладывается упорядоченное движение их в направлении оси X. Скорости такого упорядоченного движения обозначим u₁ и u₂. Согласно соотношению Эйнштейна вычисление коэффициентов диффузии D₁₂ и D₂₁ сводится к вычислению подвижностей молекул газов. Этим методом мы и воспользуемся.

Вычислим подвижность В₁ молекул первого газа. Для этого рассмотрим какую-либо одну молекулу этого газа, которую назовем молекулой 1. Решим сначала следующую задачу. Какая постоянная сила F₁ должна действовать на

молекулу 1, чтобы поддерживать ее регулярное движение с постоянной скоростью u₁? Если эта сила будет найдена, то подвижность В₁ найдется из соотношения

.

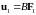Ясно, что сила F₁ в среднем должна уравновешиваться силами ударов, действующими на молекулу 1 при столкновениях. При ее вычислении можно отвлечься от изменения концентраций п₁ и п₂ в пространстве и считать эти концентрации постоянными. Тогда столкновения молекулы 1 с молекулами того же (первого) газа можно не принимать во внимание. Они движутся с той же упорядоченной скоростью u₁, а потому столкновения с ними не вносят никакого вклада в величину интересующей нас силы. Надо учесть столкновения только с молекулами второго газа.

Пусть z₁₂ — число столкновений, претерпеваемых молекулой 1 в одну секунду с молекулами второго газа, а — изменение ее импульса при одном столкновении. Полное изменение импульса молекулы 1 в одну секунду в результате столкновений с молекулами второго газа будет . Если у этой величины изменить знак и усреднить ее по всем столкновениям, то мы и получим интересующую нас силу F₁. Среднее значение произведения двух величин, вообще говоря, нельзя заменять произведением средних значений этих величин. Однако, если сделать такую замену, то это может сказаться только на несущественном численном коэффициенте порядка единицы. Поэтому в целях упрощения вычислений примем

.

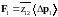Нам нужно определить среднее число столкновений . Ранее мы получали соотношение для пробной частицы в поле неподвижных частиц . Нам, следовательно, нужно учесть, что движутся все частицы. Поэтому необходимо учесть, что при столкновениях играет роль не абсолютная скорость рассматриваемой частицы, а ее скорость относительно молекулы, с которой она сталкивается. Выделим мысленно группу молекул, которые движутся относительно выделенной молекулы с одной и той же относительной скоростью v_{i отн}. Пусть n_i — число таких молекул в единице объема. Число столкновений z_i выделенной молекулы с молекулами рассматриваемой группы в единицу времени можно найти по формуле . Тогда среднее число столкновений выделенной молекулы со всеми остальными молекулами найдется суммированием этого выражения по всем скоростным группам, т. е. по всем возможным значениям индекса i:

.

Введя среднюю относительную скорость

,

получим .

Теперь рассмотрим, что будет, если сталкивающиеся молекулы различны. Пусть одна молекула сорта 1 с массой m₁ и радиусом r₁ движется в среде молекул сорта 2 с массами т₂, радиусами r₂, и концентрацией п₂. В полученной нами формуле нужно заменить 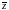на , σ – на , а средняя относительная скорсоть будет вычисляться по формуле

.

(Кому интересно, это можно получить исходя из максвелловского распределения по скоростям). Тогда среднее число столкновений дается выражением

.

Что касается величины , то при усреднении выпадет та часть ее, которая связана с тепловым движением. Поэтому от теплового движения молекулы 1 можно отвлечься и написать 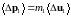. Точно так же можно отвлечься от теплового движения молекулы 2, с которой сталкивается молекула 1. Таким образом, задача свелась к рассмотрению столкновения двух молекул с массами т₁ и т₂, которые в лабораторной системе отсчета движутся со скоростями u₁ и u₂. Центр масс этих молекул движется со скоростью

.

Если молекулы считать идеально упругими шарами, то в системе центра масс они рассеиваются сферически симметрично. Это означает, что в системе центра масс средние скорости упорядоченного движения молекул после столкновения равны нулю. Значит, в лабораторной системе обе эти скорости будут равны V. Поэтому для среднего изменения скорости при столкновении получим

,

а потому ?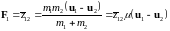

где μ – приведенная масса.

Учтем теперь, что . Если бы это было не так, то нарушилось бы постоянство полной концентрации частиц п, что привело бы к макроскопическому движению всего газа. С учетом этого

,

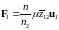а потому .

Подставляя среднее число столкновений молекулы, получим

.

Окончаельно для коэффициента диффузии можем записать

.

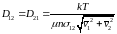В эту формулу не входят концентрации ни первого, ни второго газа. Отсюда следует, что коэффициент концентрационной диффузии газов не зависит от концентрации компонентов газовой смеси. Этот вывод подтверждается опытом.