5. Стационарное течение жидкости по прямолинейной трубе. Формула Пуазейля.

П усть вязкая несжимаемая жидкость течет вдоль прямолинейной цилиндрической трубы радиуса R. Линии тока в таком случае параллельны оси трубы. Если выделить произвольную бесконечно узкую трубку тока, то из условия несжимаемости (неразрывности струи) следует, что скорость течения v будет одна и та же вдоль всей трубки тока — скорость жидкости не может меняться вдоль трубы, так как ее поперечное сечение постоянно. Но она, конечно, может изменяться с изменением расстояния r от оси трубы. Таким образом, скорость жидкости v является функцией радиуса r. Примем ось трубы за ось X, направленную в сторону течения. Выделим в трубе произвольную бесконечно короткую цилиндрическую часть длины dx и радиуса r. На ее боковую поверхность в направлении движения действует касательная сила внутреннего трения . Кроме того, на основания цилиндра в том же направлении действует сила разности давлений . При стационарном течении сумма этих двух сил должна обращаться в нуль, а потому

.

Скорость v(r), а с ней и производная dv/dr не меняются с изменением х. Поэтому должна быть постоянной и производная dp/dx, причем эта производная должна быть равна (p₂ – p₁)/l, где p₁ — давление на входе трубы, p₂ — на выходе, а l — длина трубы. В результате приходим к уравнению

.

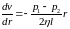Интегрируя его, получим

.

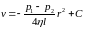Постоянная интегрирования С определится из условия, что на стенке трубы, т. е. при r = R скорость v должна обращаться в нуль. Это дает

.

Скорость v максимальна на оси трубы, где она достигает значения

.

При удалении от оси скорость v меняется по параболическому закону.

Подсчитаем расход жидкости, т. е. количество ее, ежесекундно протекающее через поперечное сечение трубы. Масса жидкости, ежесекундно протекающая через кольцевую площадку с внутренним радиусом r и внешним r + dr, равна dQ = 2πrdr∙ρv. Подставляя сюда выражение для v и интегрируя, находим искомый расход жидкости

.

Расход жидкости пропорционален разности давлений p₁ – p₂, четвертой степени радиуса трубы и обратно пропорционален длине трубы и коэффициенту вязкости жидкости. Эти закономерности были установлены экспериментально и независимо друг от друга в 1839 г. Гагеном и в 1840 г. Пуазейлем (1799—1869). Гаген исследовал движение воды в трубах, Пуазейль — течение жидкостей в капиллярах. Полученная формула для расхода называется формулой Пуазейля, хотя сам Пуазейль и не выводил ее, он исследовал вопрос только экспериментально. На формуле Пуазейля основан еще один из экспериментальных методов определения коэффициентов вязкости жидкостей (измеряем расход при прочих известных величинах, вычисляем вязкость).

Формулу для расхода можно представить в виде . С другой стороны, можно ввести среднюю скорость потока , определив ее с помощью соотношения . Сравнивая эти два выражения, получаем

.

Формула Пуазейля справедлива только для ламинарных течений жидкости. Ламинарным называется такое течение, когда частицы жидкости движутся вдоль прямолинейных траекторий, параллельных оси трубы. При больших скоростях ламинарное течение становится неустойчивым и переходит в турбулентное течение, с которым мы познакомимся дальше. К турбулентным течениям формула Пуазейля неприменима.

Кинетическая энергия, ежесекундно переносимая потоком жидкости через поперечное сечение трубы, определяется выражением

.

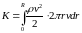После подстановки найденного значения для скорости v и интегрирования, получим

.

При этом работа, производимая над жидкостью в единицу времени разностью давлений p₁ – p₂, определяется выражением 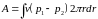или

.

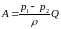Такую же по величине, но противоположную по знаку работу производят силы внутреннего трения, так как при стационарном течении кинетическая энергия жидкости остается неизменной: А' = –A. С помощью формулы для v₀ можно исключить разность давлений p₁ – p₂ и получить

.

Полученные формулы позволяют ответить на вопрос, когда при течении жидкости по трубе можно пренебречь силами вязкости и, следовательно, применять уравнение Бернулли. Для этого, очевидно, необходимо, чтобы потеря кинетической энергии жидкости, обусловленная действием сил вязкости, была пренебрежимо мала по сравнению с кинетической энергией самой жидкости, т. е. . Это приводит к условию

.

Здесь буквой ν обозначена так называемая кинематическая вязкость, т. е. отношение

.

Величину η, когда ее надо отличить от кинематической вязкости, называют динамической вязкостью.

6. Турбулентность и гидродинамическая неустойчивость

До сих пор при изучении движений жидкости мы имели в виду так называемые ламинарные (слоистые) течения жидкостей и газов. Особенностью ламинарного течения является его регулярность. Течение при сохранении ламинарности может изменяться лишь вследствие изменения сил, действующих на жидкость, или внешних условий, в которых она находится. Так, при ламинарном течении в прямолинейной трубе постоянного поперечного сечения частицы жидкости движутся вдоль прямолинейных траекторий, параллельных оси трубы. Однако при достаточно больших скоростях ламинарное течение оказывается неустойчивым и переходит в так называемое турбулентное течение. Турбулентное течение – это такое течение, гидродинамические характеристики которого (скорость, давление, а для газов — плотность и температура) быстро и нерегулярно изменяются во времени (флуктуируют). Частицы жидкости совершают нерегулярные, неустановившиеся движения по сложным траекториям, что приводит к интенсивному перемешиванию между слоями движущейся жидкости. Примерами могут служить движение воды в бурном горном потоке, водопаде или за кормой быстроплывущего корабля, движение дыма, выходящего из трубы и т. п. Такие быстрые и нерегулярные изменения происходят не из-за изменений действующих сил или внешних условий, а вследствие неустойчивости ламинарных течений при определенных условиях. Неустойчивость ламинарных течений и возникновение турбулентности – очень сложные вопросы, еще далекие до окончательного решения. Рассмотрение их далеко выходит за рамки нашего курса, подробнее вы будете рассматривать его в курсе гидродинамики. Тем не менее имеет смысл привести простейший пример, когда вопрос об устойчивости ламинарного течения решается элементарно.

Таким примером может служить установившееся ламинарное движение жидкости между двумя вращающимися коаксиальными цилиндрами, которое мы уже рассматривали, при больших числах Рейнольдса. Число Рейнольдса является важной характеристикой течения жидкости, остановимся на нем подробнее. Это одно из так называемых безразмерных критериев подобия течений, с которыми вы познакомитесь позже. Оно определяется соотношением

,

где l – характерный размер течения (например, радиус сечения трубы или поперечный размер обтекаемого тела), v₀ – характерная скорость потока (например, скорость жидкости вдали от обтекаемого тела или средняя скорость течения). Если рассматривать физический смысл этого параметра, то по порядку величины число Рейнольдса есть отношение кинетической энергии жидкости к потере ее, обусловленной работой сил вязкости на характерной длине. Действительно, кинетическая энергия жидкости . Силу вязкости найдем, умножая величину вязкого напряжения ηv₀/l на характерную площадь l². Это дает ηv₀l. Произведение этой силы на характерную длину определяет по порядку величины работу сил вязкости 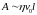. Тогда отношение кинетической энергии к работе составит величину порядка

,

а это и есть число Рейнольдса. Таким образом, число Рейнольдса определяет относительную роль инерции и вязкости жидкости при течении. При больших числах Рейнольдса основную роль играет инерция, при малых – вязкость.

Число Рейнольдса, конечно, определено не вполне четко, поскольку оно содержит характерную длину и характерную скорость, которые сами определены не четко. Это число определено лишь по порядку величины. Если размеры тела в разных направлениях примерно одинаковы, то особой неопределенности не возникает. Если же это не так, то в качестве характерной длины могут быть выбраны разные величины, которые могут отличаться друг от друга значительно. Например, при течении жидкости по трубе за характерную длину можно взять длину трубы, ее радиус или какую-либо промежуточную величину. Соответствующие числа Рейнольдса могут отличаться на много порядков. Какое из этих чисел взять — зависит от поставленной задачи. Так рассматривая течение в цилиндрической трубе, мы вывели условие , при выполнении которого силами вязкости можно пренебречь. Величину, стоящую слева в формуле можно рассматривать как число Рейнольдса, если за характерную длину принять . В рассматриваемом случае характерный размер зависит как от длины трубы, так и от ее радиуса. При таком выборе получается рассмотренное ранее условие, справедливое для всех, а не только геометрически подобных круглых труб (т. е. труб с постоянным отношением R/l).

Итак, при больших числах Рейнольдса вязкостью жидкости можно пренебречь, считая жидкость идеальной. Для идеальных жидкостей, из-за отсутствия тангенциальных напряжений, зависимость скорости от расстояния до оси вращения может быть произвольной: v = v(r). Но уже ничтожной вязкости достаточно, чтобы спустя некоторое время после начала движения установилось вполне определенное распределение скоростей вдоль радиуса, а именно

.

Однако для последующих рассуждений конкретизация вида функции v = v(r) не обязательна. В невозмущенном потоке частицы жидкости движутся по окружностям с определенной угловой скоростью . Рассмотрим какой-либо элемент жидкости, вращающийся по окружности радиуса r₀. На него действует центростремительная сила , создаваемая разностью давлений окружающей жидкости. Введя момент количества движения , запишем выражение для силы в виде

.

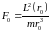Допустим теперь, что под влиянием какого-то бесконечно малого случайного толчка рассматриваемый элемент жидкости сместился в новое положение, находящееся на расстоянии r от оси вращения. Можно предполагать, что толчок был совершен в направлении от или к оси вращения, так как, если движение жидкости неустойчиво по отношению к возмущениям специального вида, то оно неустойчиво вообще. Момент силы такого толчка относительно оси вращения равен нулю. Результирующая сил давления окружающей жидкости также не дает момента, поскольку она направлена к оси вращения. Поэтому при смещении элемента момент его количества движения сохранится, т. е. и в новом положении будет L(r₀). Чтобы сместившийся элемент равномерно вращался по окружности радиуса r, на него должна действовать центростремительная сила . Между тем единственная сила, которой он подвержен, есть сила давления окружающей жидкости, а она равна . Если эта сила не равна F'₀, то элемент жидкости не удержится на новой круговой орбите, куда он попал. Он будет либо возвращаться к исходной орбите, либо удаляться от нее. В первом случае движение жидкости устойчиво, во втором — неустойчиво.

Допустим, например, что r >r₀. Если F > F'₀, т. е. L²(r) > L²(r₀), то давление окружающей жидкости больше того, которое требуется для удержания сместившегося элемента жидкости на окружности радиуса r. Сместившийся элемент вернется на исходную окружность — движение устойчиво.

Если же F < F'₀, т. е. L²(r) < L²(r₀), то силы давления окружающей жидкости недостаточно, чтобы удержать элемент на окружности радиуса r. Элемент жидкости будет уходить еще дальше — движение неустойчивое.

Если r <r₀, то рассуждая аналогично, найдем, что при L²(r) < L²(r₀) движение устойчиво, а при L²(r) > L²(r₀) — неустойчиво. В обоих случаях критерий устойчивости можно выразить неравенством

,

или .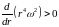

Таким образом, для устойчивости необходимо, чтобы величина 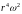монотонно возрастала при удалении от оси вращения. Если цилиндры вращаются в противоположные стороны, то это невозможно. Действительно, в этом случае на поверхностях цилиндров угловая скорость ω имеет противоположные знаки. Так как ω — непрерывная функция r, то она должна обращаться в нуль в какой-то промежуточной точке. В этой точке величина равна нулю, т. е. достигает минимума. По разные стороны от нее производная 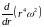имеет противоположные знаки, т. е. условие устойчивости не может выполняться. Значит, если цилиндры вращаются в противоположные стороны, то движение жидкости неустойчиво. Оно будет неустойчивым и в том случае, когда внутренний цилиндр вращается, а наружный покоится. Действительно, на поверхности наружного цилиндра , а на поверхности внутреннего . Поэтому с увеличением r величина не может монотонно возрастать, и движение неустойчиво. Если же вращается наружный цилиндр, а внутренний покоится, то установившееся вращение жидкости будет устойчивым. В этом случае с удалением от оси вращения угловая скорость ω возрастает, а потому тем более будет возрастать . Теперь становится понятным, почему при измерении коэффициента внутреннего трения по методу, описанному когда мы рассматривали понятие вязкости, должен вращаться наружный, а не внутренний цилиндр. В противном случае вращение жидкости между цилиндрами было бы неустойчивым.

4. Приведенное исследование было выполнено без учета вязкости жидкости. Силы вязкости, уменьшая кинетическую энергию жидкости, всегда препятствуют развитию неустойчивостей. Область неустойчивости ламинарного течения сужается. Ограничимся этим общим замечанием о роли сил вязкости, так как нашей целью было только показать на простейшем примере, что ламинарное течение жидкости не всегда устойчиво.

5. При возрастании скорости течения ламинарное движение переходит в турбулентное. Скорость, при которой это происходит, называется критической. Вместо скорости лучше пользоваться безразмерной величиной — числом Рейнольдса. Граничное значение числа Рейнольдса, при котором ламинарный режим течения сменяется турбулентным, называется критическим числом Рейнольдса и обозначается Re_Kp. Значение Re_Kp зависит от конфигурации тел, обтекаемых жидкостью, а также от степени возмущенности самого ламинарного течения. Так, при течении по прямолинейной трубе круглого сечения , если труба непосредственно присоединена к водопроводу и не приняты специальные предосторожности для уменьшения возмущенности воды у края трубы (а — радиус трубы, v—средняя скорость течения). Величину начальной возмущенности можно уменьшить, применяя трубы с гладкими стенками и закругленными краями. Кроме того, следует присоединять их к большому баку с водой и подождать, пока вода в нем не успокоится. Таким путем удается добиться затягивания ламинарного режима в трубах до значительно больших Re_Kp, например до .

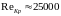ЯВЛЕНИЯ ПЕРЕНОСА В ГАЗАХ